[DB] Normalization

In general, the goal of relational database design is to generate a set of relation schemas that allows us to store information without unnecessary redundancy, yet also allows us to retrieve information easily. This is accomplished by designing schemas that are in an appropriate normal form.

This post introduces a formal approach to relational database design based on the notion of functional dependencies. We then define normal forms in terms of functional dependencies and other types of data dependencies.

Overview of Normalization

Suppose that the tables instructor and department are combined via natural join.

$\mathbf{Fig\ 1.}$ Redundant Relational Designs

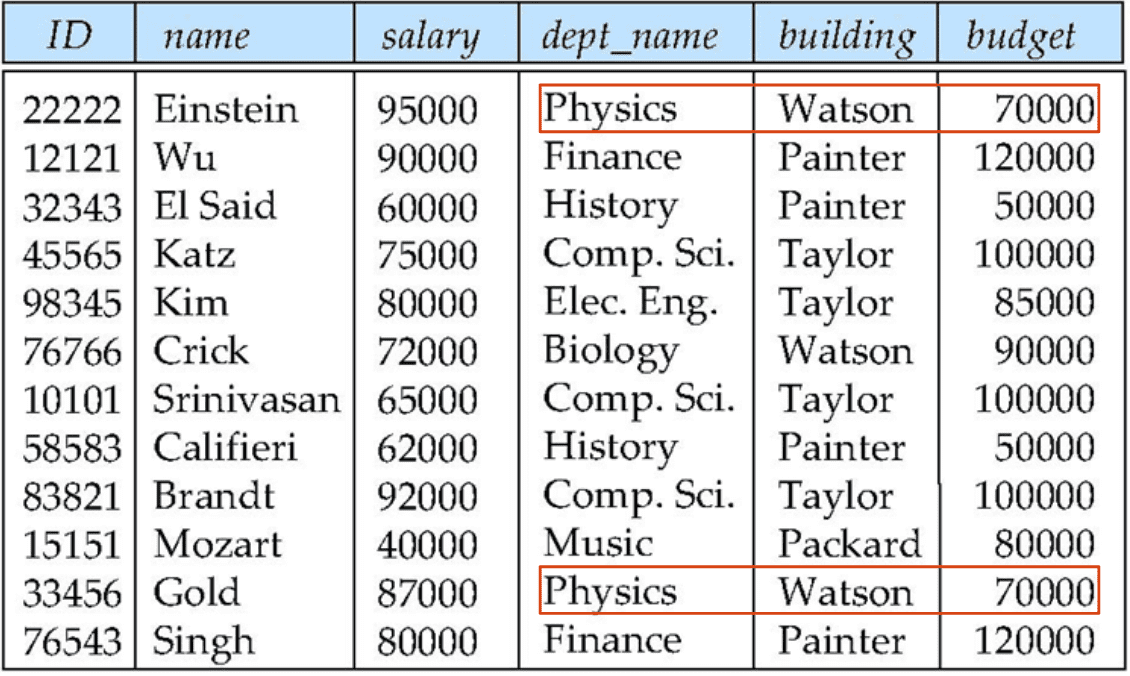
This relation design is not good because:

• There are repetitions of information.
• NULL values must be used when a new department with no instructor is added.

However, not all combined schemas result in repetitions of information.

Decomposition

The only way to avoid the repetition-of-information problem in the previous example is to decompose it into two schemas: instructor and department. However, not all decompositions are helpful. Consider the decomposition

Relation	Attributes
employee	ID, name, street, city, salary

into the following two schemas:

Relation	Attributes
employee1	ID, name
employee2	name, street, city, salary

The problem arises when there are multiple employees with the same name.

$\mathbf{Fig\ 2.}$ We cannot reconstruct the original employee relation; so, this is a lossy decomposition.

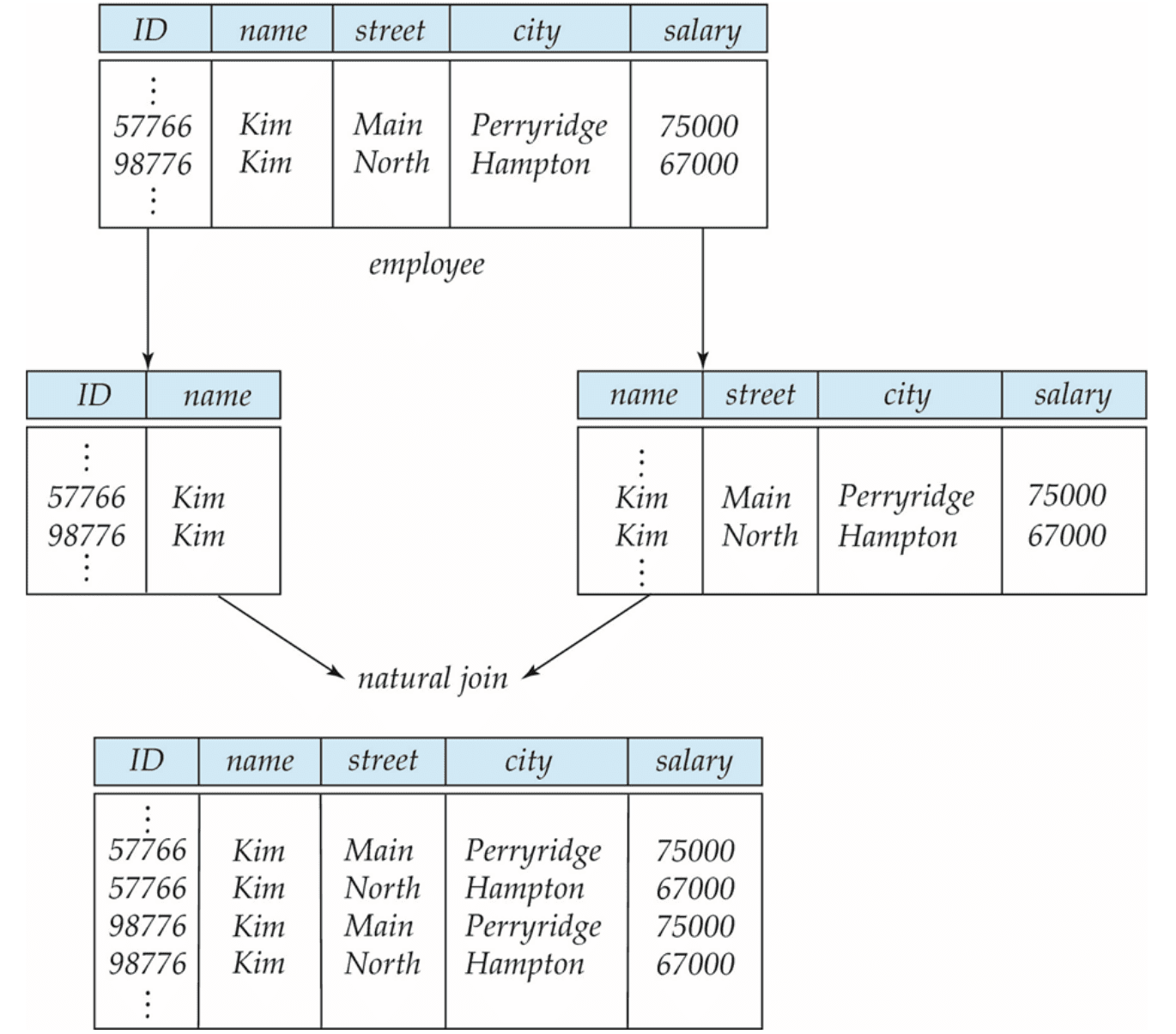
We can indicate that a certain street, city, and salary pertain to someone named Kim, but we are unable to distinguish which of the Kims. Such decomposition is unable to represent certain important facts about the relation before the decomposition. This kind of decomposition is referred to as a lossy decomposition. Conversely, those that are not are referred to as lossless decomposition.

Lossless Decomposition

The formal definitions of lossy/lossless decomposition are given as follows:

$\color{blue}{\mathbf{Definition.}}$ Lossy and Lossless Decomposition
Let $r$ be a relation, $R$ be a relation schema of $r$ and let $R_1$, $R_2$ form a decomposition of $R$. In other words, $R = R_1 \cup R_2$. The decomposition is said to be lossless if there is no loss of information by replacing $R$ with $R_1 \cup R_2$. Equivalently, $$ \Pi_{R_1} (r) \bowtie \Pi_{R_2} (r) = r $$ Conversely, a decomposition is said to be lossy if $$ r \subsetneq \Pi_{R_1} (r) \bowtie \Pi_{R_2} (r) $$

$\mathbf{Fig\ 2.}$ The visualization of definition

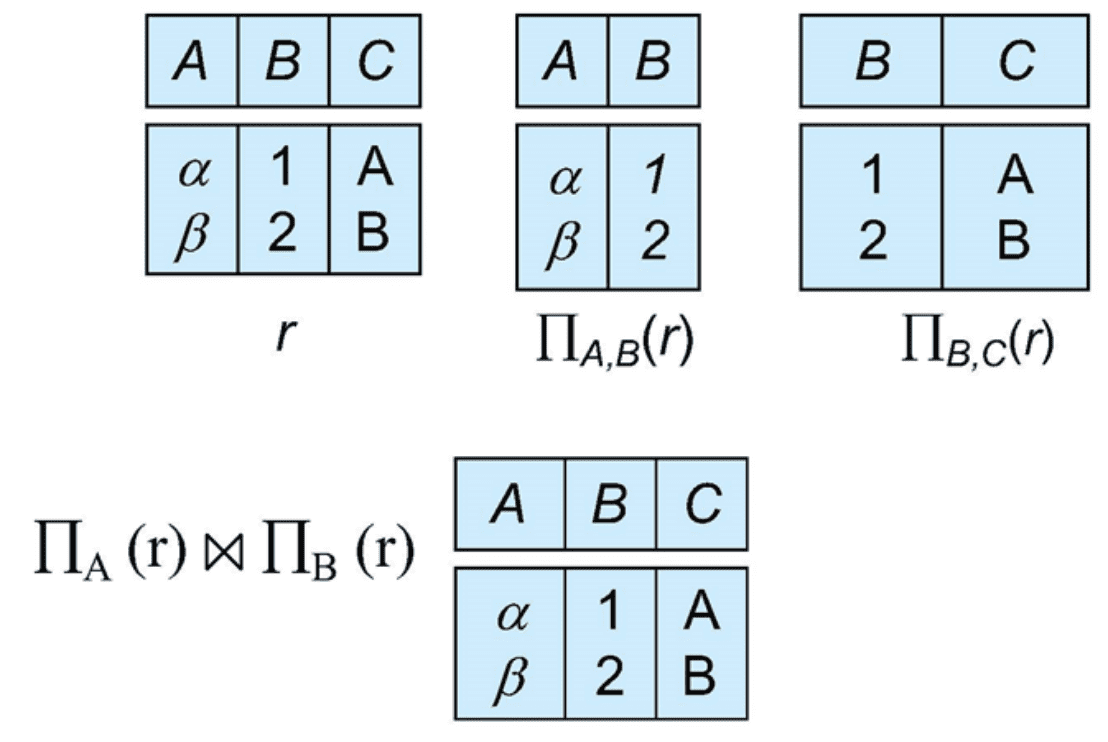
And functional dependencies, discussed in the following section, can be used to show when certain decompositions are lossless. Consider the decomposition of $R$ into $R_1$​, $R_2$​. The sufficient condition for it to be a lossless decomposition is that at least one of the following dependencies is in $F^+$:

• $R_1 \cap R_2​ \to R_1$​
• $R_1 \cap R_2​ \to R_2$​

This is because if the entities in one of the decomposed relations are uniquely determined by the join key $R_1 \cap R_2$​, it will preserve the number of entries in the Cartesian product (i.e., $1 \times x = x$).

Normalization Theory

We are now in a position to define a general methodology for deriving a set of schemas each of which is in good form; that is, does not suffer from the repetition-of-information problem. The method for designing a relational database is to use a process commonly known as normalization. The goal is to generate a set of relation schemas \(\{R_1, \cdots, R_n\}\) that allows us to store information of relation $R$ without unnecessary redundancy, yet also allows us to retrieve information easily.

Functional Dependency

There are usually a variety of constraints on the data in the real world. For example,

• Students and instructors are uniquely identified by their ID;
• Each student and instructor has only one name;

An instance of a relation that satisfies all such real-world constraints is called a legal instance of the relation; a legal instance of a database is one where all the relation instances are legal instances. Some of the most commonly used types of real-world constraints can be represented formally as keys (superkeys, candidate keys, and primary keys), or as functional dependencies. A functional dependency is a generalization of the notion of a key.

Definition

$\color{blue}{\mathbf{Definition.}}$ Functional Dependency
Consider a relation schema $r(R)$, and let $\alpha, \beta \subseteq R$ be sets of attributes. Given an instance of $r(R)$, the instance is said to satisfy a functional dependency $\alpha \to \beta$ if for all pairs of tuples $t_1$​ and $t_2$​ in the instance: $$ t_1​[\alpha]=t_2​[\alpha] \implies t_1​[\beta]=t_2​[\beta]. $$ The functional dependency $F$ is said to hold on schema $r(R)$ if every legal instance of $r(R)$ satisfies the functional dependency. And a functional dependency is referred to as trivial if it is satisfied by all instances of a relation. In general, $\alpha \to \beta$ is trivial if $\beta \subseteq \alpha$.

Note that a specific instance of a relation schema may satisfy a functional dependency even if the functional dependency does not hold on all legal instances.

• e.g., A specific instance of instructor may, by chance, satisfy name → ID

One easy way to understand the concept of functional dependency is to interpret $\alpha \to \beta$ as:

If values of $\alpha$ is given, then values of $\beta$ is uniquely determined.

Keys and Functional Dependencies

Functional dependencies allow us to express constraints that cannot be expressed using superkeys.

• $K$ is a superkey for relational schema $r(R)$ if and only if the functional dependency $K \to R$ holds on $r(R)$.
• $K$ is a candidate key for $r(R)$ if and only if the functional dependency $K \to R$ holds on $r(R)$, and for any $L \subsetneq K$, $L \not\to R$.

For example,

• in_dep (ID, name, salary, dept_name, building, budget).
• We expect these functional dependencies to hold:
  • dept_name → budget because for each department there is a unique budget amount.
  • ID → building
• but would not expect the following to hold:
  • dept_name → salary

Use of Functional Dependencies

Functional dependencies can be used to:

• Test relations to see if they are legal under a given set of functional dependencies
• Specify constraints on the set of legal relations

Functional Dependency Theory

Closure

Given a set $F$ of functional dependencies, there are certain other functional dependencies that are logically implied by $F$.

The set of all functional dependencies logically implied by $F$ is called the closure of $F$, and is denoted as $F^+$.

$\color{blue}{\mathbf{Definition.}}$ Closure of a Set of Functional Dependencies
Given a set $F$ of functional dependencies, there are certain other functional dependencies that are logically implied by $F$. For example, if $A \to B$ and $B \to C$, then we can infer that $A \to C$. The set of all functional dependencies logically implied by $F$ is the closure of $F$. We denote the closure of $F$ by $F^+$. Hence, all of functional dependencies in $F$ are contained in $F^+$.

Armstrong’s Axioms

For any set $F$ of functional dependencies, the closure $F^+$ of $F$ can be obtained by repeatedly applying Armstrong’s axioms.

$\color{blue}{\mathbf{Definition.}}$ Armstrong's Axioms
Let $\alpha$, $\beta$, $\gamma$, and $\delta$ be sets of attributes of a relation schema $R$ with the set of functional dependency $F$.

• Reflexive rule: $\beta \subseteq \alpha \implies \alpha \to \beta$
• Augmentation rule: $\alpha \to \beta \implies \forall \gamma: \gamma \alpha \to \gamma \beta$
• Transitivity rule: $\alpha \to \beta \wedge \beta \to \gamma \implies \alpha \to \gamma$

Note that these rules are both

• Sound: generating only functional dependencies that actually hold
• Complete: generating all functional dependencies that hold

Although Armstrong’s axioms are complete, it is tiresome to use them directly for the computation of $F^+$. To simplify matters further, we list additional rules.

$\color{#bf1100}{\mathbf{Remark.}}$ Addtional rules
Some additional rules can be inferred from Armstrong’s axioms:

• Union rule: $\alpha \to \beta \wedge \alpha \to \gamma \implies \alpha \to \beta \gamma$
• Decomposition rule: $\alpha \to \beta \gamma \implies \alpha \to \beta \wedge \alpha \to \gamma$
• Pseudo-transitivity rule: $\alpha \to \beta \wedge \gamma\beta \to \delta \implies \alpha \gamma \to \delta$

The following pseudocode shows a procedure that demonstrates formally how to use Armstrong’s axioms to compute $F^+$:

F_closure = F
REPEAT
  FOR EACH f IN F_closure
    APPLY reflexivity AND augmentation ON f
    ADD TO F_closure
  FOR EACH PAIR f1, f2 IN F_closure
    IF f1 AND f2 APPLY transitivity
    THEN ADD TO F_closure
UNTIL (F_closure CONVERGE)

• Note that the LHS & RHS of a functional dependency are both subsets of $R$. Since a set of size $n$ has $2^n$ subsets, there are a total of $2^n \times 2^n = 2^{2n}$ possible functional dependencies, where $n$ is the number of attributes in $R$. Thus, the procedure is guaranteed to terminate, though it may be very lengthy.

Closure of Attribute Sets

We say that an attribute $\beta$ is functionally determined by $\alpha$ if $\alpha \to \beta$.

Given a set of attributes $\alpha$, we can also define the closure of $\alpha$ under $F$ (denoted by $\alpha^+$) as the set of attributes that are functionally determined by $\alpha$ under $F$. It is obtained by the following procedure:

A_closure = A
REPEAT
  FOR EACH β -> 𝛄 IN F
    IF β IN A_closure
    THEN ADD 𝛄 TO A_closure
UNTIL (A_closure CONVERGE)

$\color{green}{\mathbf{Example.}}$ Suppose we are given a relation schema r(A,B,C,G,H,I) and the set of functional dependencies F = { A → B, A → C, CG → H, CG → I, B → H}. Then, (AG)+ is given by

1. result = AG
2. result = ABCG since A → B and A → C
3. result = ABCGH since CG → H and CG ⊆ ABCG
4. result = ABCGHI since CG → I and CG ⊆ ABCGH

Then, it can be used for testing if AG is candidate key or not.

1. Is AG a superkey? In other words, AG → R (that is, R = (AG)+)?
2. Is Is any subset of AG a superkey?

It can be used for various purposes:

• Testing for superkey
  • Testing if $\alpha$ is a superkey can be done by checking if $R \subseteq \alpha^+$.
• Testing functional dependencies
  • Testing if a functional dependency $\alpha \to \beta$ is in $F^+$ can be done by checking $\beta \subseteq \alpha^+$.
• Computing the closure $F^+$
  • $F^+$ can be obtained by finding $\gamma^+$ for each $\gamma \subseteq R$, and for each $S \subseteq \gamma^+$, yielding a function dependency $\gamma \to S$.

Canonicial Cover

Whenever a user performs an update on a relation, the database system must ensure that the update does not violate any functional dependencies. (If an update violates any functional dependencies in the set $F$, the system must roll back the update.)

The effort spent in checking for violations in functional dependencies can be reduced by testing on only a simplified set of functional dependencies that has the same closure as the given set. This is the canonical cover of the functional dependencies.

Extraneous Attributes

To define the canonical cover, the extraneous attributes must be first defined. When removing an atrribute from a functional dependency:

• Removing an attribute from the left side of a functional dependency could make it a stronger constraint.
  • For example, for $AB \to C$ and removing $B$, we get the possibly stronger result $A \to C$
• Removing an attribute from the right side of a functional dependency could make it a weaker constraint.
  • For example, for $AB \to CD$ and removing $C$, we get the possibly weaker result $AB \to D$

But, depending on what our set $F$ of functional dependencies happens to be, these discardings can be done safely:

• For example, \(F = \{ AB \to C, A \to D, D \to C \}\)
  • We can show that $F$ logically implies $A \to C$, making $B$ extraneous in $AB \to C$.
• For example, \(F = \{ AB \to CD, A \to C \}\)
  • Even after replacing $AB \to CD$ by $AB \to D$, we can still infer $AB \to C$, thus $AB \to CD$

Hence, for a set $F$ of functional dependencies and a functional dependency $\alpha \to \beta \in F$, the extraneous attribute $A$ as follows:

$\color{blue}{\mathbf{Definition.}}$ Extraneous Attributes
Consider a set $F$ of functional dependencies and a functional dependency $\alpha \to \beta \in F$. An attribute of functional dependency in $F$ is said to be extraneous if it can be removed without changing its closure $F^+$. Formally, attribute $A$ is extraneous in $\alpha$ or in $\beta$ if

• if $A \in \alpha$
  $F$ logically implies $(F - \{ \alpha \to \beta \}) \cup \{ (\alpha - A) \to \beta \}$
• if $A \in \beta$
  $(F - \{ \alpha \to \beta \}) \cup \{ \alpha \to (\beta - A) \}$ logically implies $F$.

Notice that implication in the opposite direction is trivial in each of the cases above, since a stronger functional dependency always implies a weaker one.

For testing if an attribute $A$ in the functional dependency $\alpha \to \beta \in F$ is extraneous:

• Testing if $A \in \alpha$ extraneous in $\alpha$
1. Let $\gamma = \alpha - A$;
2. Compute $\gamma^+$ under $F$;
3. If $\beta \subseteq \gamma^+$, $A$ is extraneous in $\alpha$;
• Testing if $A \in \beta$ extraneous in $\beta$
1. Let $F^\prime = (F - \{\alpha \to \beta\}) \cup \{ \alpha \to (\beta - A) \}$;
2. Compute $\alpha^+$ under $F^\prime$;
3. If $A \in \alpha^+$, $A$ is extraneous in $\beta$;

$\color{green}{\mathbf{Example.}}$ Suppose we are given a relation schema r(A,B,C,G,H,I) and the set of functional dependencies F = { AB → CD, A → E, E → C}. To check if C is extraneous in AB → CD, we:

• compute the attribute closure of AB under F' = {AB → D, A → E, E → C}.
• The closure is ABCDE, which includes CD.
• This implies that C is extraneous.

Definition

Having defined the concept of extraneous attributes, we can explain how we can construct a canonical cover:

$\color{blue}{\mathbf{Definition.}}$ Canonical cover
A canonical cover for $F$ is a set of dependencies $F_c$​ that satisfies all of the followings:

• $F$ logically implies all dependencies in $F_c$​;
• $F_c$​ logically implies all dependencies in $F$;
• None of the attributes in $F_c$​ is extraneous;
• Each left side of all functional dependencies in $F_c$​ is unique;
  • i.e., $\forall \alpha_1 \to \beta_1​, \alpha_2​ \to \beta_2 \in F_c : \alpha_1​ \neq \alpha_2$​

Computing Canonical Covers

To compute a canonical cover for $F$:

F_c = F
REPEAT
  FOR EACH ɑ -> β1, ɑ -> β2 IN F_c
    APPLY union rule /* ɑ -> β_1, β_2 */
    REPLACE TO F
  FOR EACH f in F_c
    IF EXISTS (extraneous attribute A) IN f
    REMOVE A FROM f
UNTIL (F_c CONVERGE)

• Note that the union rule may become applicable after some extraneous attributes have been deleted, so it has to be re-applied.
• Since the algorithm permits a choice of any extraneous attribute, it is possible that there may be several possible canonical covers for a given $F$.
  • However, any $F_c$ is minimal in a certain sense — it does not contain extraneous attributes, and it combines functional dependencies with the same LHS.

$\color{green}{\mathbf{Example.}}$ Suppose we are given a relation schema r(A,B,C) and the set of functional dependencies F = { A → BC, B → C, A → B, AB → C}. Then, F_c is given by

1. result = {A → BC, B → C, AB → C} by union rule;
2. result = {A → BC, B → C} since A is extraneous;
3. result = {A → B, B → C} since C is extraneous;

Dependency Preservation

Testing functional dependency constraints each time the database is updated can be costly. Thus, it is useful to design the database in a way that constraints can be tested efficiently.

When decomposing a relation, it may be no longer possible to do the testing without having to perform a Cartesian product of join operations. In particular, if testing a functional dependency can be done by considering just one relation, then the cost of testing this constraint is low.

A decomposition that makes it computationally hard to enforce functional dependency is said to be not dependency preserving.

Conversely, if functional dependencies of the original relation can be checked on the decomposed relations without the need of Cartesian product or join operations, is said to be dependency preserving.

$\color{blue}{\mathbf{Definition.}}$ Dependency Preservation
Let $F$ be the set of functional dependencies on schema $R$, and let $R_1, \cdots, R_n$ be a decomposition of $R$. Let $F_i$ be a restriction of $F$ to $R_i$, i.e. a set of all functional dependencies in $F^+$ that include only attributes of $R_i$.

The decomposition is dependency preserving if the following holds: $$ \left( \bigcup_{i=1}^n F_i \right)^+ = F^+. $$

Testing for Dependency Preservation

The following algorithm checks if a dependency $\alpha \to \beta$ is preserved in a decomposition of $R$ into \(D = \{ R_1, \cdots, R_n \}\).

result = ɑ
REPEAT
  FOR EACH R[i] IN D
    t = CLOSURE(result INTERSECT R[i]) INTERSECT R[i]
    result = result UNION t
UNTIL (result CONVERGE)

This sequence of steps is equivalent to computing the closure of result under $F_i$.

If result contains all attributes in $\beta$, then the functional dependency $\alpha \to \beta$ is presereved.

This method takes polynomial time, instead of exponential time required when using the definition directly.

Multivalued Dependencies (MVDs)

Functional dependencies rule out certain tuples from being in a relation. For example, if $A \to B$, then we can’t have two tuples with the same $A$ value but different $B$ values.

Multivalued dependency, however, do not rule out the existence of certain tuples; instead, they require that other tuples of a certain form be present in the relation.

$\color{blue}{\mathbf{Definition.}}$ Multivalue Dependency
Let $r(R)$ be a relation schema and let $\alpha \subseteq R$ and $\beta \subseteq R$. The multivalued dependency $$ \alpha \twoheadrightarrow \beta $$ ("$\alpha$ multidetermines $\beta$") holds on $R$ if, in any legal instance of relation $r(R)$, for all pairs of tuples $t_1, t_2 \in R$ such that $t_1 [\alpha] = t_2 [\alpha]$, there exists tuples $t_3, t_4 \in R$ that satisfies all of the followings:

• $t_1 [\alpha] = t_2 [\alpha] = t_3 [\alpha] = t_4 [\alpha]$
• $t_3 [\beta] = t_1 [\beta]$
• $t_3 [R - \beta] = t_2 [R - \beta]$
• $t_4 [\beta] = t_2 [\beta]$
• $t_4 [R - \beta] = t_1 [R - \beta]$

Note that $\alpha \twoheadrightarrow \beta$ is trivial if $\beta \subseteq \alpha$ or $\beta \cup \alpha = R$. And the following is a tabular representation of the multivalued dependency $\alpha \twoheadrightarrow \beta$:

$\mathbf{Fig\ 2.}$ Tabular representation of $\alpha \twoheadrightarrow \beta$.

Intuitively, $\alpha \twoheadrightarrow \beta$ says that the relationship between $\alpha$ and $\beta$ is independent of the relationship between $\alpha$ and $R - \beta$. In other words, the attributes $\beta$ and $R - \beta$ are dependent on $\alpha$, but independent of each other. Databases with non-trivial multivalued dependencies thus exhibit redundancy.

Informally, the following alternative definition is also possible:

$\color{blue}{\mathbf{Definition.}}$ Alternative definition of MVD
Let $R$ be a relation schema with a set of attributes that are partitioned into 3 nonempty subsets $X$, $Y$, $Z$. Then, $X \twoheadrightarrow Y$ holds on $R$ if any only if for all possible relations $r(R)$: $$ \begin{aligned} & \langle x_1, y_1, z_1 \rangle, \langle x_1, y_2, z_2 \rangle \in r \\ \implies & \langle x_1, y_2, z_1 \rangle, \langle x_1, y_1, z_2 \rangle \in r \end{aligned} $$ Note that since the behavior of $Y$ and $Z$ are identical, it follows that $X \twoheadrightarrow Y \Leftrightarrow X \twoheadrightarrow Z$.

$\color{green}{\mathbf{Example.}}$ Consider the schema r (ID, dept_name, street, city) and an example relation on that schema:

$\mathbf{Fig\ 2.}$ An example of redundancy in a relation on a BCNF schema.

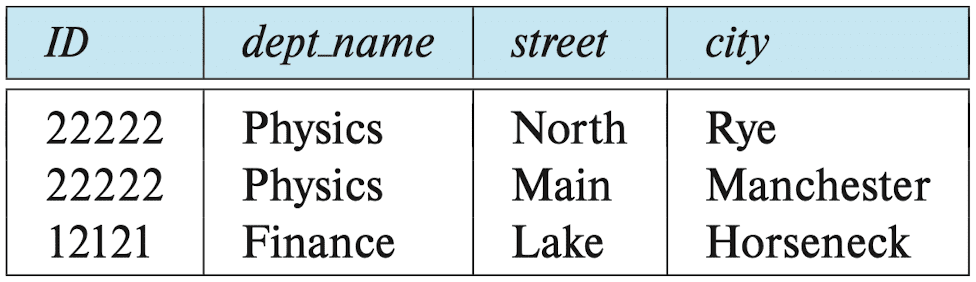
We must repeat the dept_name once for each address that an instructor has, and we must repeat the address for each dept_name with which an instructor is associated. This repetition is unnecessary, since the relationship between an instructor and his address is independent of the relationship between that instructor and dept_name. (In other words, ID →→ street, city and ID →→ dept_name)

From the definition of MVDs, we can derive the following rule:

$\color{red}{\mathbf{Thm.}}$ Every functional dependency is also a multivalued dependency: $$ \alpha \to \beta \implies \alpha \twoheadrightarrow \beta $$

$\color{red}{\mathbf{Proof.}}$

Every FD is an MVD because if $\alpha \to \beta$, then swapping $\beta$’s between tuples that agree on $\alpha$ doesn’t create new tuples.

Specifically, suppose $\alpha \to \beta$, and let $t_1 = (a, b, c)$ and $t_2 = (a, d, e)$ are given. By the functional dependency, $b = d$. Therefore, $t_3 = t_1 = (a, d, c)$ and $t_4 = t_2 = (a, b, e)$ naturally exist without considering additional tuples.

\[\tag*{$\blacksquare$}\]

Use of multivalued dependencies

Multivalued dependencies can be used to:

• Test relations to determine whether they are legal under a given set of functional and multivalued dependencies.
• Specify constraints on the set of legal relations.

If a relation $r$ fails to satisfy a given multivalued dependency, a relation $r^\prime$ that satisfies the multivalued dependency can be constructed by adding additional tuples to $r$.

Closure: Armstrong’s axioms for MVD

The closure $D^+$ of $D$ is defined as the set of all functional and multivalued dependencies logically implied by $D$. Similar to closure of FDs, we can compute $D^+$ from $D$, using the formal definitions of functional dependencies and multivalued dependencies. We can manage with such reasoning for very simple multivalued dependencies, which seem to be most common in practice.

For complex dependencies, it is better to reason about sets of dependencies using a system of inference rules called Armstrong’s axioms for MVD:

$\color{blue}{\mathbf{Definition.}}$ Armstrong's Axioms for MVD
Let $\alpha$, $\beta$, $\gamma$, and $\delta$ be sets of attributes of a relation schema $R$ with the set of multivalue dependency $D$.

• Complementation rule: $\alpha \twoheadrightarrow \beta \implies \alpha \twoheadrightarrow R - \beta$
• Augmentation rule: $\alpha \twoheadrightarrow \beta \wedge \gamma \subseteq \delta \implies \alpha\delta \twoheadrightarrow \beta\gamma$
• Transitivity rule: $\alpha \twoheadrightarrow \beta \wedge \beta \twoheadrightarrow \gamma \implies \alpha \twoheadrightarrow \gamma - \beta$
• Replication rule: $\alpha \to \beta \implies \alpha \twoheadrightarrow \beta$
• Coalescence rule: $\alpha \twoheadrightarrow \beta \wedge \exists \delta: (\delta \cap \beta = \varnothing \wedge \delta \to \gamma \wedge \gamma \subseteq \beta) \implies \alpha \to \gamma$

$\color{blue}{\mathbf{Proof.}}$ Soundness

Since complementation rule and replication rule are trival, this proof only shows the soundness of remaining 3 rules.

Augmentation rule

Assume $\alpha \twoheadrightarrow \beta$ and $\gamma \subseteq \delta$. Then,

• For any tuples $t_1, t_2 \in R$ with $t_1[\alpha] = t_2[\alpha]$ and $t_1[\delta] = t_2[\delta]$ (that is, $t_1[\alpha\delta] = t_2[\alpha\delta]$), there exist tuples $t_3, t_4 \in R$ such that
  • $t_3[\alpha\delta] = t_4 [\alpha\delta] = t_1[\alpha\delta]$
  • thus $t_3[\alpha] = t_4[\alpha] = t_1[\alpha]$ and $t_3[\delta] = t_4[\delta] = t_1[\delta]$
  • due to $\alpha \twoheadrightarrow \beta$
    • $t_3[\beta] = t_1[\beta]$
    • $t_3[R - \beta] = t_2[R - \beta]$
    • $t_4[\beta] = t_2[\beta]$
    • $t_4[R - \beta] = t_1[R - \beta]$
  • due to $\gamma \subseteq \delta$
    • $t_3[\delta] = t_1[\delta] \implies t_3[\gamma] = t_1[\gamma]$
    • $t_3[R - \beta] = t_2[R - \beta] \implies t_3[R - \beta\gamma] = t_2[R - \beta\gamma]$ since $R - \beta\gamma \subseteq R - \beta$
    • $t_4[\delta] = t_2[\delta] \implies t_4[\gamma] = t_4[\gamma]$
    • $t_4[R - \beta] = t_1[R - \beta] \implies t_4[R - \beta\gamma] = t_1[R - \beta\gamma]$ since $R - \beta\gamma \subseteq R - \beta$

This implies $\alpha\delta \twoheadrightarrow \beta\gamma$.

Transitivity rule

Assume $\alpha \twoheadrightarrow \beta$ and $\beta \twoheadrightarrow \gamma$. Then,

• For any tuples $t_1, t_2 \in R$ with $t_1[\alpha] = t_2[\alpha]$, there exist tuples $t_3, t_4 \in R$ such that
  • $t_3 [\alpha] = t_4[\alpha] = t_1[\alpha] = t_2[\alpha]$
  • $t_3 [\beta] = t_1[\beta]$
  • $t_3 [R - \beta] = t_2[R - \beta] \implies t_3 [\gamma - \beta] = t_2[\gamma - \beta]$ since $\gamma - \beta \subseteq R - \beta$.
  • $t_4 [\beta] = t_2[\beta]$
  • $t_4 [R - \beta] = t_1[R - \beta] \implies t_4 [\gamma - \beta] = t_1[\gamma - \beta]$ since $\gamma - \beta \subseteq R - \beta$.
• From $\beta \twoheadrightarrow \gamma$, there exist $t_5, t_6 \in R$ such that
  • for $t_3[\beta] = t_1[\beta]$
    • $t_5 [\beta] = t_1[\beta]$
    • $t_5 [\gamma] = t_3[ \gamma ]$
    • $t_5 [R - \gamma] = t_1 [R - \gamma]$
    • that is, $t_5 [R - (\gamma - \beta)] = t_1 [R - (\gamma - \beta)]$ since $R - (\gamma - \beta) = (R - \gamma) \cup \beta$
  • for $t_4[\beta] = t_2[\beta]$
    • $t_6 [\beta] = t_2[\beta]$
    • $t_6 [\gamma] = t_4[ \gamma ]$
    • $t_6 [R - \gamma] = t_2 [R - \gamma]$
    • that is, $t_6 [R - (\gamma - \beta)] = t_2 [R - (\gamma - \beta)]$ since $R - (\gamma - \beta) = (R - \gamma) \cup \beta$

Hence, there exist tuples $t_5, t_6 \in R$ such that

• $t_5[\alpha] = t_1[\alpha] = t_2[\alpha]$ since for any attribute $A \in \alpha$
  • If an attribute $A \in (R - \gamma) \cap \alpha$
    • $t_5 [A] = t_1[A]$ by $t_5 [R - \gamma] = t_1 [R - \gamma]$
  • If an attribute $A \in \gamma \cap \alpha$
    • $t_5 [A] = t_3[A]$ by $t_5 [\gamma] = t_3[ \gamma ]$
    • $t_3 [A] = t_1[A]$ by $t_3[\alpha] = t_1[\alpha]$
• $t_6[\alpha] = t_1[\alpha] = t_2[\alpha]$ analogously
• $t_5[ \gamma - \beta ] = t_3 [ \gamma - \beta ] = t_2[\gamma - \beta]$
• $t_5[ R - (\gamma - \beta)] = t_1 [ R - (\gamma - \beta)]$
• $t_6[ \gamma - \beta ] = t_4 [ \gamma - \beta ] = t_1[\gamma - \beta]$
• $t_6[ R - (\gamma - \beta)] = t_2 [ R - (\gamma - \beta)]$

Coalesence rule

Assume $\alpha \twoheadrightarrow \beta$ and there exists $\delta \subset R$ such that $\delta \cap \beta = \varnothing$, $\delta \to \gamma$, $\gamma \subseteq \beta$. Then,

• For any tuples $t_1, t_2 \in R$ with $t_1[\alpha] = t_2[\alpha]$,
  • By $\alpha \twoheadrightarrow \beta$, there exist tuples $t_3 \in R$ such that
    • $t_1 [\alpha] = t_2[\alpha] = t_3 [\alpha]$
    • $t_3[\beta] = t_1[\beta] \implies t_3[\gamma] = t_1[\gamma]$ since $\gamma \subseteq \beta$
    • $t_3[R - \beta] = t_2[R - \beta] \implies t_3[\delta] = t_2[\delta]$ since $\delta \subseteq R - \beta$
  • From $\delta \to \gamma$, $t_3[\delta] = t_2[\delta]$ implies $t_3 [\gamma] = t_2 [\gamma]$.
  • That is, $t_1[ \gamma] = t_2[\gamma]$

This implies $\alpha \to \gamma$.

\[\tag*{$\blacksquare$}\]

We can further simplify calculating the closure of $D$ by using the following rules, derivable from the previous ones:

$\color{#bf1100}{\mathbf{Remark.}}$ Addtional rules
Some additional rules can be inferred from Armstrong’s axioms:

• Union rule: $\alpha \twoheadrightarrow \beta \wedge \alpha \twoheadrightarrow \gamma \implies \alpha \twoheadrightarrow \beta \gamma$
• Intersection rule: $\alpha \twoheadrightarrow \beta \wedge \alpha \twoheadrightarrow \gamma \implies \alpha \twoheadrightarrow \beta \cap \gamma$
• Difference rule: $\alpha \twoheadrightarrow \beta \wedge \alpha \twoheadrightarrow \gamma \implies \alpha \twoheadrightarrow \beta - \gamma \wedge \alpha \twoheadrightarrow \gamma - \beta$

$\color{#bf1100}{\mathbf{Proof.}}$ Soundness

Union rule

\[\begin{aligned} & \alpha \twoheadrightarrow \gamma & \\ & \alpha \twoheadrightarrow \alpha\gamma & \textrm{ augmentation rule } \\ & \alpha \twoheadrightarrow \beta & \\ & \alpha\gamma \twoheadrightarrow \beta\gamma & \textrm{ augmentation rule } \\ & \alpha\gamma \twoheadrightarrow R - \alpha\beta\gamma & \textrm{ complementation rule } \\ & \alpha \twoheadrightarrow R - \alpha\beta\gamma & \textrm{ transitivity rule } \\ & \alpha \twoheadrightarrow \beta\gamma & \textrm{ complementation rule } \\ \end{aligned}\]

Intersection rule

\[\begin{aligned} & \alpha \twoheadrightarrow R - \gamma & \textrm{ complementation rule } \\ & \alpha \twoheadrightarrow R - \beta & \textrm{ complementation rule } \\ & \alpha \twoheadrightarrow R - (\beta \cap \gamma) & \textrm{ union rule } \\ & \alpha \twoheadrightarrow \beta \cap \gamma & \textrm{ complementation rule } \\ \end{aligned}\]

Difference rule

This rule can be simply derived from complementation rule and intersection rule. By complementation rule, $\alpha \twoheadrightarrow R - \gamma = \gamma^c$. By intersection rule between $\alpha \twoheadrightarrow \gamma^c$ and $\alpha \twoheadrightarrow \beta$, $\alpha \twoheadrightarrow \beta \cap \gamma^c = \beta - \gamma$ holds.

\[\tag*{$\blacksquare$}\]

Lossless Decomposition

Let $r(R)$ be a relation schema, and let $D$ be a set of functional and multivalued dependencies on $R$. Let $r_1(R_1)$ and $r_2(R_2)$ form a decomposition of $R$. This decomposition of $R$ is lossless if and only if at least one of the following multivalued dependencies is in $D^+$:

\[\begin{gathered} R_1 \cap R_2 \twoheadrightarrow R_1 \\ R_1 \cap R_2 \twoheadrightarrow R_2 \end{gathered}\]

Reference

[1] Silberschatz, Abraham, Henry F. Korth, and Shashank Sudarshan. “Database system concepts.” (2011).
[2] C.Beeri, R.Fagin, and J.H.Howard, “A Complete Axiomatization for Functional and Multivalued Dependencies in Database Relations”, Proc. of 1977 ACM SIGMOD Conference