[DB] Normal Forms

In general, the goal of relational database design is to generate a set of relation schemas that allows us to store information without unnecessary redundancy, yet also allows us to retrieve information easily. This is accomplished by designing schemas that are in an appropriate normal form.

$\mathbf{Fig\ 1.}$ Venn diagram of normal forms (source: Can Güney Aksakalli)

Boyce–Codd Normal Form (BCNF)

Definition

$\color{blue}{\mathbf{Definition.}}$ Boyce–Codd Normal Form (BCNF)
A relation schema $R$ is in Boyce-Codd normal form (BCNF) with respect to a set of functional dependencies $F$ if for all functional dependencies $\alpha \to \beta \in F^+$, where $\alpha, \beta \subseteq R$, at least one of the following holds:

• $\alpha \to \beta$ is trivial. (i.e., $\beta \subseteq \alpha$)
• $\alpha$ is a superkey of $R$. (i.e., $\alpha \to R$)

For example, consider in-dep(ID​, name, salary, dept_name​, building, budget), and the set of functional dependencies \(F = \{\text{ID} \to \{\text{name}, \text{dept_name}, \text{salary}\}, \text{dept_name} \to \{\text{building}, \text{budget}\}\}\). This is not in BCNF because

• dept_name → building, budget holds in in-dep, but
• dept_name is not a superkey.

But when decomposing in_dept into instructor and department are both in BCNF.

Testing for BCNF

We need algorithms for the generation of designs that are in appropriate normal form. Testing of a relation schema $R$ to see if it satisfies BCNF can be simplified in some cases.

Testing functional dependency

To check if a nontrivial functional dependency $\alpha \to \beta$ causes a violation of BCNF:

• Compute $\alpha^+$.
• Verify that $R \subseteq \alpha^+$, i.e., $\alpha^+$ is a superkey of $R$.

Testing relation schema decomposition

Let $R$ be a relation schema, and $R_1​, \cdots, R_n$​ be a decomposition of $R$. Let $F$ be the set of functional dependencies.

• For every set of attributes $\alpha \subseteq R_i$​, compute $\alpha^+$.
• Verify that either $\alpha^+ \cap (R_i - \alpha) = \varnothing$ or $R_i \subseteq \alpha^+$.
  • If the condition is violated by some $\alpha$, the dependency $\alpha \to (\alpha^+ - \alpha) \cap R_i​ \in F^+$ but $\alpha$ is not a superkey as $R_i \nsubseteq \alpha^+$. Hence $R_i$​ violates BCNF.

Decomposition into BCNF

Let $R$ be a schema that is not in BCNF, and let $\alpha \to \beta$ be the functional dependency that causes a violation in BCNF. Then we decompose $R$ into:

• $\alpha \cup \beta$
• $R - (\beta - \alpha)$ (In most cases, $\beta - \alpha = \beta$.)

$\color{green}{\mathbf{Example.}}$ In our example of in_dep,

• $\alpha = \text{dept_name}$
• $\beta = \text{building}, \text{budget}$

and in_dep is replaced by

• $(\alpha \cup \beta) = (\text{dept_name}, \text{building}, \text{budget})$
• $(R - (\beta - \alpha)) = (\text{ID}, \text{name}, \text{dept_name}, \text{salary})$

When we decompose a schema that is not in BCNF, it may be that one or more of the resulting schemas are not in BCNF. In such cases, further decomposition is required, the eventual result of which is a set of BCNF schemas.

Or, in the following alternative algorithm is also possible:

result = R
done = FALSE
WHILE (NOT done)
  IF (there is a schema R_i in result that is not in BCNF):
    let non-trivial ɑ -> β holds on R_i such that 
      (R_i ⊈ ɑ+) ∧ (ɑ ∩ β = ∅);
    result = (result - R_i) ∪ (R_i - β) ∪ (ɑ, β)
  ELSE
    done = TRUE

Note that it generates not only BCNF, but also a lossless decomposition. When we replace a schema $R_i$ with $(R_i − \beta)$ and $(\alpha, \beta)$, the dependency $\alpha \to \beta$ holds, and $(R_i - \beta) \cap (\alpha, \beta) = \alpha$.

$\color{green}{\mathbf{Example.}}$ Suppose we have a database design using the class (course_id, title, dept_name, credits, sec_id, semester, year, building, room_number, capacity, time_slot_id) relation.

The set of functional dependencies that we need to hold on this schema are:

• course_id → title, dept_name, credits
• building, room_number → capacity
• course_id, sec_id, semester, year → building, room_number, time_slot_id

A candidate key for this schema is {course_id, sec_id, semester, year}.

BCNF decomposition:

• course_id is not a superkey;
• we replace class by;
  • course (course_id, title, dept_name, credits)
  • class-1 (course_id, sec_id, semester, year, building, room_number, capacity, time_slot_id)
• {building, room_number} is not a superkey;
• we replace class-1 by;
  • classroom (building, room_number, capacity)
  • section (course_id, sec_id, semester, year, time_slot_id)

Although the BCNF algorithm ensures that the resulting decomposition is loss-less, note that it is possible to have a schema and a decomposition that was not generated by the algorithm, that is in BCNF, and is not lossless.

BCNF and Dependency Preservation

However, it is not always possible to achieve both BCNF and dependency preservation. Consider a schema: dept_advisor(s_ID, i_ID, dept_name) with function dependencies i_ID → dept_name and s_ID, dept_name → i_ID. Note that dept_advisor is not in BCNF since i_ID is not a superkey. Following our rule for BCNF decomposition, we get:

• (s_ID, i_ID)
• (i_ID, dept_name)

But any of the decomposed relation does not include all the attributes in the dependency s_ID, dept_name → i_ID; it is not dependency preserving. Because dependency preservation is usually considered desirable, we consider another normal form, weaker than BCNF, that will allow us to preserve dependencies. That normal form is called the third normal form.

Third Normal Form (3NF)

Definition

$\color{blue}{\mathbf{Definition.}}$ Third Normal Form (3NF)
A relation schema $R$ is in third normal form (3NF) with respect to a set of functional dependencies $F$ if for all functional dependencies $\alpha \to \beta \in F^+$, where $\alpha, \beta \subseteq R$, at least one of the following holds:

• $\alpha \to \beta$ is trivial. (i.e., $\beta \subseteq \alpha$)
• $\alpha$ is a superkey of $R$. (i.e., $\alpha \to R$)
• Each attribute $A$ in $\beta - \alpha$ is contained in a candidate key for $R$. Note that each attribute may be in a different candidate key.

If a relation is in BCNF, then it is in 3NF also. The third condition is a minimal relaxation to BCNF to ensure dependency preservation.

For example, consider dept_advisor(s_ID, i_ID, dept_name), and the set of functional dependencies i_ID → dept_name, s_ID, dept_name → i_ID. Then, the candidate keys are (s_ID, dept_name) and (s_ID, i_ID). Hence, although $R$ is not in BCNF, $R$ is in 3NF.

Testing for 3NF

Unlike testing for BCNF, testing for 3NF need not check all functional dependencies in $F^+$; it only requires to check only functional dependencies in $F$ itself.

Let $R$ be a relation schema, and let $F$ be the set of functional dependencies.

1. For every functional dependency $\alpha \to \beta \in F$, compute $\alpha^+$.
2. If $\alpha \to R$, $\alpha \to \beta$ does not violate 3NF.
3. Otherwise if $\alpha$ is not a superkey of $R$, verify if each attribute in $\beta$ is contained in a candidate key of $R$.

However, this test is rather more expensive, since it involves finding candidate keys. Indeed, testing for 3NF has been shown to be NP-complete (NP-hard) by Jou et al. 1982 because the problem of finding all of the keys of a relation has been shown to be NP-complete.

Interestingly, decomposition into 3NF can be done in polynomial time.

Decomposition into 3NF

The following algorithm ensures

• Each relation schema $R_i$ is in 3NF;
• The decomposition is dependency preserving and lossless-join;

$\mathbf{Fig\ 2.}$ Decomposition into 3NF.

Proof: the algorithm indeed preserves dependencies

The 3NF algorithm ensures the preservation of dependencies by explicitly building a schema for each dependency in a canonical cover.

Proof: the algorithm indeed constructs loss-less decomposition

The 3NF algorithm ensures that the decomposition is a lossless decomposition by guaranteeing that at least one schema contains a candidate key for the schema being decomposed. Consider the dependency-preserving 3NF decomposition of schema $R$ with the set of dependencies $F$, $R_1, \cdots, R_n$ by the algorithm, and a legal instance $r$ of $R$. Let $X$ be a candidate key for $R$. Let $j = \Pi_X (r) \bowtie \Pi_{R_1} (r) \bowtie \cdots \bowtie \Pi_{R_n} (r)$. We already know that $r \subseteq j$. But we should prove that $r = j$.

Claim: if $t_1$ and $t_2$ are two tuples in $j$ such that $t_1 [X] = t_2 [X]$, then $t_1 = t_2$. In other words, $X \to j$. This implies that the size of $\Pi_X (j)$ is equal to the size of $j$ since $t_1 \neq t_2 \wedge t_1 [X] = t_2 [X]$ is impossible. Moreover, as $X \to R$, $\Pi_X(j) = \Pi_X(r) = r$. Thus this claim proves the final statement.

Proof: To prove this claim, we use the following inductive argument. Let $F^\prime = F_1 \cup F_2 \cup \dots \cup F_n$, where each $F_i$ is the restriction of $F$ to the schema $R_i$. Consider the use of the attribute closure algorithm to compute $X^+$ under $F^\prime$. We use induction on the number of times that the for loop in this algorithm is executed:

• Basis
  $\mathrm{result} = X$, and hence $t_1 [\mathrm{result}] = t_2 [\mathrm{result}]$ holds given that $t_1 [X] = t_2 [X]$.
• Induction
  Let $t_1 [\mathrm{result}] = t_2 [\mathrm{result}]$ be true at the end of the $k$-th execution of the for loop. Suppose the functional dependency considered in the $(k + 1)$-th execution of the for loop is $\beta \to \gamma$ and that $\beta \subseteq \mathrm{result}$. $\beta \subseteq \mathrm{result}$ implies that $t_1 [\mathrm{result}] = t_2 [\mathrm{result}]$. The facts that $\beta \to \gamma$ holds for some attribute set $R_i$ and that $t_1 [R_i]$ & $t_2 [R_i]$ are in $\Pi_{R_i} (r)$ imply that $t_1 [\gamma] = t_2 [\gamma]$ is also true. Since $\gamma$ is now added to the $\mathrm{result}$ by the algorithm, we know that $t_1[\mathrm{result}] = t_2[\mathrm{result}]$ is true at the end of the $(k + 1)$-th execution of the for loop.

Since the decomposition is dependency-preserving and $X$ is a key for $R$, all attributes in $R$ are in $\mathrm{result}$ when the algorithm terminates.

Proof: the algorithm indeed produces a 3NF design

To see that the algorithm indeed produces a 3NF design, consider a schema $R_i$ in the decomposition. For any non-trivial $\gamma \to \delta$ in the set of functional dependencies of $R_i$, we may assume that $\gamma$ is not a super-key without loss of generality. (If $\gamma$ is superkey, it already satisfies the second condition of 3NF.) As we have to show that each attribute of $\delta - \gamma$ is contained in the candidate key of $R_i$, again, it suffices to functional dependencies whose right-hand side consists of a single attribute and thus we may assume $\delta = B$ without loss of generality.

Assume that the dependency that generated $R_i$ in the synthesis algorithm is $\alpha \to \beta$. $B$ must be in $\alpha$ or $\beta$, since $B$ is in $R_i$ and $\alpha \to \beta$ generated $R_i$. Let us consider the three possible cases:

• $B \in \alpha \cap \beta$;
  • This case is impossible since the dependency $\alpha \to \beta$ cannot be in $F_c$ as $B$ would be extraneous in $\beta$.
• $B \in \alpha$ only;
  • Since $\alpha$ is a candidate key of $R_i$, the third definition of 3NF is satisfied.
• $B \in \beta$ only;
  • $\gamma$ is a superkey;
    • The second condition of 3NF is satisfied.
  • $\gamma$ is not a superkey;
    • $\alpha$ must contain some attribute not in $\gamma$. If not, i.e. $\alpha \subseteq \gamma$, $\gamma \to \alpha$ holds then $\gamma$ becomes a superkey of $R_i$.
    • Since $\gamma \to B \in F^+$, it must be derivable from $F_c$ by deriving $\gamma^+$. Note that the attribute closure algorithm cannot uses $\alpha \to B$ because this implies $\alpha \in \gamma^+$ which is impossible as $\gamma$ is not a superkey but $\alpha$ is superkey of $R_i$.
    • Since $\alpha \to \beta - B$ and $B \in \beta - \alpha$, $\alpha \to \alpha\beta - B$ holds from augmentation rule. Since $\gamma \subseteq \alpha \beta = R_i$ but $\gamma \to B$ is nontrivial ($B \notin \gamma$), $\gamma \subseteq \alpha \beta - B$.
    • That is, $\alpha \to \alpha\beta - B \to \gamma \to B$ by transitivity rule.
    • This implies that $B$ is extraneous in the RHS of $\alpha \to \beta$, which is impossible since $\alpha \to \beta \in F_c$.
    • Thus, if $B \in \beta$, $\gamma$ must be a superkey.

Comparison of BCNF and 3NF

• It is always possible to decompose a relation into a set of relations that are in BCNF such that:
  • The decomposition is lossless.
• It is always possible to decompose a relation into a set of relations that are in 3NF such that:
  • The decomposition is lossless.
  • The decomposition preserves dependencies.

	BCNF	3NF
Redundancy	Less than 3NF	More than BCNF
Lossless Decomposition	Always guaranteed	Always guaranteed
Dependency Preservation	Not guaranteed	Always guaranteed

Aside: Equivalent Definition

$\color{red}{\mathbf{Theorem.}}$ Equivalent Definition to 3NF
Let a prime attribute be one that appears in at least one candidate key. We say that an attribute $A$ is transitively dependent on $\alpha$ if $\alpha \to \beta$ and $\beta \to A$ holds, but $\beta \to \alpha$ does not hold, $A \notin \alpha$ and $A \notin \beta$. A relation schema $R$ is in 3NF with respect to a set $F$ of functional dependencies if there are no non-prime attributes $A$ in $R$ for which $A$ is transitively dependent on a key for $R$.

$\color{red}{\mathbf{Proof.}}$

1. Suppose $R$ is in 3NF according to the original definition. We show that it is in 3NF according to the definition in this statement. Suppose this is false. That is, there exists $A$ be a nonprime attribute in $R$ that is transitively dependent on a key for $R$. Then there exists $\alpha \to \beta$ where $\alpha$ is a key for $R$, $\beta \to A$ holds but $\beta \to \alpha$ doesn’t hold, $\beta \to A$, $A \notin \alpha$, and $A \notin \beta$. But this violates the definition of 3NF, which is the contradiction:

• $\beta \to A$ is non-trivial;
• $\beta \to R$ does not hold as $\beta \not\to \alpha$. If $\beta$ is a key, $\beta \to \alpha$ should be satisfied;
• $A - \beta = A$ is not contained in the candidate keys of $R$ since $A$ is non-prime;

2. Suppose $R$ is in 3NF according to the definition in this statement. We show that it is in 3NF according to the original definition. Let $\alpha \to \beta$ be any non-trivial FDs on $R$. Suppose $R$ is not in 3NF according to the original definition. Then there is a non-trivial FD $\alpha \to \beta$ such that

• $\alpha$ is not a superkey;
• Some $A$ in $\beta - \alpha$ is non-prime; note that $\alpha \to A$.

But we can show that such $A$ must be transitively dependent on a key for $R$ in this case, which is the contradiction to the definition of $R$:

• Let $\gamma$ be a candidate key for $R$; then $\gamma \to \alpha$;
• Since $\alpha$ is not a superkey, $\alpha \not\to \gamma$;
• $A$ is non-prime, thus $A \notin \gamma$;
• $A \notin \alpha$ as $A \in \beta - \alpha$;

Thus $A$ is transitively dependent on $\gamma$.

\[\tag*{$\blacksquare$}\]

Fourth Normal Form (4NF)

Motivation: Higher Normal Forms

Using functional dependencies to decompose schemas may not be sufficient to avoid the redundancy; there are database schemas in BCNF that do not seem to be sufficiently normalized. Consider a relation:

• inst_info (ID, child_name, phone)
  • An instructor may have more than one phone and can have multiple children.

  • Example instance:

    

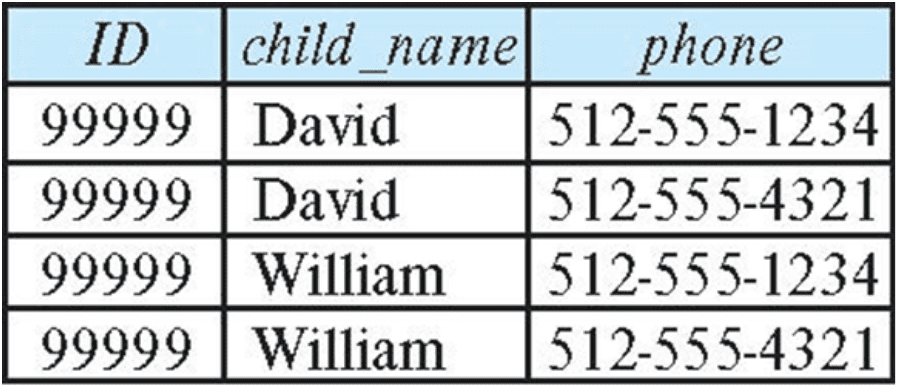
    $\mathbf{Fig\ 2.}$ Relation inst_info.

  • There is no non-trivial functional dependency, and therefore the relation is in BCNF.
  • Insertion anomalies: if we add a phone 981-992-3443 to ID 99999, we need to add two tuples
    • (99999, David, 981-992-3443)
    • (99999, William, 981-992-3443)

• It is better to decompose inst_info into inst_child and inst_phone: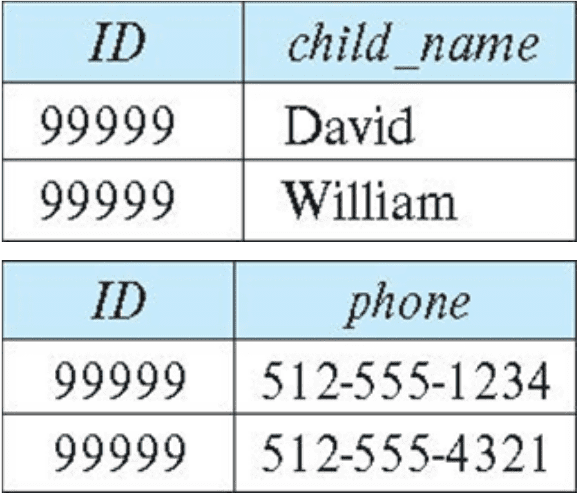

  

  $\mathbf{Fig\ 3.}$ Decomposition of inst_info.

Definition

The definition of 4NF differs from the definition of BCNF in only the use of multivalued dependencies. Therefore, every 4NF schema is in BCNF.

$\color{blue}{\mathbf{Definition.}}$ Fourth Normal Form (4NF)
Let $R$ be a relation schema, and $D$ be a set of functional and multivalued dependencies of $R$. Let $D^+$ be the closure of $D$. A relation schema $R$ is in Fourth normal form (4NF) if, for all multivalued dependencies $\alpha \twoheadrightarrow \in D^+$, at least one of the followings hold:

• $\alpha \twoheadrightarrow \beta$ is trivial. (i.e., $\beta \subseteq \alpha$ or $\alpha \cup \beta = R$)
• $\alpha$ is a superkey of $R$. (i.e., $\alpha \to R$)

Note that every 4NF schema is in BCNF, which is obvious from the fact that every functional dependency is also a multivalued dependency:

\[\alpha \to \beta \implies \alpha \twoheadrightarrow \beta\]

Decomposition into 4NF

The analogy between 4NF and BCNF applies to the algorithm for decomposing a schema into 4NF. It is identical to the BCNF decomposition algorithm, except that it uses MVDs and uses the restriction of $D^+$ to $R_i$:

$\color{blue}{\mathbf{Definition.}}$ Restriction
The restriction of $D$ to $R_i$ is the set $D_i$ consisting of

1. All functional dependencies in $D^+$ that include only attributes of $R_i$;
2. All multivalued dependencies of the form $$ \alpha \twoheadrightarrow \beta \cap R_i $$ where $\alpha \subseteq R_i$ and $\alpha \twoheadrightarrow \beta$ is in $D^+$.

The following algorithm ensures

• Each relation schema $R_i$ is in 4NF;
• The decomposition is lossless-join;

$\mathbf{Fig\ 3.}$ Decomposition into 4NF

First Normal Form (1NF)

The E-R model allows entity sets and relationship sets to have attributes that have some degree of substructure. Specifically, it allows multivalued attributes such as phone_number and composite attributes such as an attribute address with component attributes street, city, and state.

When we create tables from E-R designs that contain these types of attributes, we eliminate this substructure. For composite attributes, we let each component be an attribute in its own right. For multivalued attributes, we create one tuple for each item in a multivalued set. In the relational model, we formalize this idea that attributes do not have any substructure, using the concept of atomicity.

Definition

$\color{blue}{\mathbf{Definition.}}$ First Normal Form (1NF)
A domain is atomic if elements of the domain are considered to be indivisible units. We say that a relation schema $R$ is in first normal form (1NF) if the domains of all attributes of $R$ are atomic.

$\mathbf{Fig\ 3.}$ Normalization to First Normal Form (1NF)

For example, identification numbers like CS101 that can be broken up into parts is an example of non-atomic domains. And a set of names is also non-atomic domain, hence a schema employee included an attribute children whose domain elements are sets of names, would not be in first normal form. Obviously, these non-atomic values complicate storage and introduce repeating groups.

But, we should note that atomicity is actually a property of how the elements of the domain are used.

• Example: Strings would normally be considered indivisible
• Suppose that students are given identification numbers which are strings of the form CS0012 or EE1127
  • If the first two characters are extracted to find the department, the domain of numbers is not atomic; not recommended because encoding of information exists in an application program rather than in the database

Moreover, nested tables are not originally supported in relational databases. Therefore, typical relational databases satisfy the first normal form.

Second Normal Form (2NF)

Definition

$\color{blue}{\mathbf{Definition.}}$ Second Normal Form (2NF)
If a relation is in the first normal form (1NF), and every non-primary-key attribute is fully functionally dependent on the primary key, then the relation is in the second normal form (2NF). Formally, a functional dependency $\alpha \to \beta$ is called a partial dependency if there is a proper subset $\gamma \subset \alpha$ such that $\gamma \to \beta$; we say that $\beta$ is partially dependent on $\alpha$. A relation schema $R$ is in second normal form (2NF) if each attribute $A$ in $R$ meets at least one of the following criteria:

• It appears in a candidate key;
• It is not partially dependent on a candidate key;

$\mathbf{Fig\ 3.}$ Normalization to Second Normal Form (2NF)

Note that every 3NF schema is in 2NF, which can be proved by the equivalent definition of 3NF. Specifically, suppose that $R$ is in 3NF and fix an arbitrary attribute $A$ of $R$.

• If $A$ is prime attribute, then it appears in a candidate key and satisfies the first condition of 2NF;
• If $A$ is non-prime attribute, $A$ is not transitively dependent on any key for $R$.
  • Therefore, it suffices to show that partial dependency $\alpha \to A$ is a transitive dependency when $A$ is non-prime and $\alpha$ is a candidate key for $R$. Suppose that $\alpha \to A$ is partial dependency; there is a proper subset $\gamma$ of $\alpha$ such that $\gamma \to A$.
  • Then, we can show that $A$ is transitively dependent on $\alpha$:
    • $\alpha \to \gamma$ since $\gamma \subset \alpha$;
    • $\beta \not\to \alpha$ since $\alpha$ is a candidate key;
    • $A \notin \alpha \wedge A \notin \gamma$ since we assume $A$ is non-prime;

Database-Design Process

So far, we have explored detailed issues regarding normal forms and normalization. A natural question that arises is how normalization integrates into the overall database design process.

We have assumed that a schema $R$ is given. In practice, there are several ways in which we could have come up with the schema $r(R)$:

• $R$ could have been generated when converting an E-R diagram to a set of tables;
• $R$ could have been a single relation containing all attributes that are of interest (called a universal relation);
  • Normalization breaks $R$ into smaller relations
• $R$ could have been the result of some ad-hoc design of relations, which we then test/convert to a normal form;

E-R Model and Normalization

When an E-R diagram is carefully designed, identifying all entities correctly, the tables generated from the E-R diagram should not need further normalization. However, in a real (imperfect) design, there can be functional dependencies from non-key attributes of an entity to other attributes of the entity.

• Example: an employee entity with
  • Attributes dept_name and building
  • Functional dependency dept_name -> building
• Good design would have made department an entity and a relationship set between employee and department.

Functional dependencies from non-key attributes of a relationship set possible, but rare; since most relationships are binary.

Denormalization for Performance

One may want to use non-normalized schema that has redundant information for performance. The penalty paid for non-normalized schema is the extra work to keep redundant data consistent. For example, displaying prerequisites along with course_id and title requires join of course with prereq.

• Alternative 1: Use a denormalized relation containing the attributes of course as well as prereq with all above attributes
  • Faster lookup
  • Extra space and extra execution time for updates
  • Extra coding work for programmers and possibility of error in extra code
• Alternative 2: Use a materialized view defined as course ⋈ prereq
  • Same as above, except the third one since keeping the view up to date is the job of the database system, not the application programmer

Other Design Issues

Some aspects of database design are not caught by normalization and can thus lead to bad database design. The followings are examples of bad database design, to be avoided:

• Instead of earnings (company_id, year, amount) with company_id, year -> amount use
  • earnings_2023, earnings_2024, earnings_2025, etc., all on the schema (company_id, earnings)
    • This is a bad idea-they’re in BCNF, but needs a new table for each year;
  • company_year (company_id, earnings_2023, earnings_2024, earnings_2025)
    • This is also a bad idea-they’re in BCNF, but requires a new attribute for each year and queries would also be more complicated, since they may have to refer to many attributes
    • But mainly used in spreadsheets for the purpose of displaying to users

References

[1] Silberschatz, Abraham, Henry F. Korth, and Shashank Sudarshan. “Database system concepts.” (2011).
[2] Jiann H. Jou and Patrick C. Fischer, “The complexity of recognizing 3NF relation schemes,” Information Processing Letters 14(4): 187–190, 1982