[DL] Batch Normalization

Batch Normalization was first proposed in ICML 2015 [1]. It performs whitening to the intermediate layers of neural networks, which is one of the most frequently used techniques in training neural networks.

---

Motivation: Feature Scaling

The most popular data preprocessing is input normalization (or, standardization) where we process the input feature distribution to have a normal distribution. This can be done by

\[\begin{aligned} \widetilde{x}_{d}^{(i)} = \frac{ x_{d}^{(i)} - \mu_d} { \sigma_d } \end{aligned}\]

for each dimension $d$ of datapoint $i$. This procedure makes our data much stable and it helps the faster convergence of loss.

Then, can we apply this technique to the neural network? When we see DNNs as feature (representation) learners, each hidden layer can be seen as new input features to the next layer. But these are not normalized. Wouldn’t it be helpful to do the feature scaling at every hidden layer?

Batch Normalization

We can normalize the input feature by normalizing the data in each dimension (each mini-batch). Since the distribution of data changes in every iteration (weights and activations), we should repeats normalization in each hidden layer.

The following figure visualizes BN in a brief and easy to understand.

Effect of BN

Batch Normalization can make training mush faster. It was understood that BN reduces internal covariate shift, i.e., the distribution of each layer’s inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models. [1]

But recently, it was uncovered that such distributional stability of layer inputs occupies little in the success of batch normalization. Instead, it can stablizes the training process of neural networks by making the optimization landscape significanlty smoother. This smoothness induces a more predictive and stable behavior of the gradients, allowing for faster training. [2]

MNIST dataset

Also, it can act as a regularizer, so that we can eliminate the need for Dropout.

Batch norm is similar to dropout in the sense that it multiplies each hidden unit by a random value at each step of training. In this case, the random value is the standard deviation of all the hidden units in the minibatch. Because different examples are randomly chosen for inclusion in the minibatch at each step, the standard deviation randomly fluctuates. Batch norm also subtracts a random value (the mean of the minibatch) from each hidden unit at each step. Both of these sources of noise mean that every layer has to learn to be robust to a lot of variation in its input, just like with dropout. Ian Goodfellow [3]

Why does BN have learnable scale and shift?

Why does batch normalization have learnable scale and shift? [4]

Normalizing the mean and standard deviation of a unit can reduce the expressibility of the neural network containing that unit as the outputs will reside in around $0$. To maintain the expressive power of the network, it is common to replace the batch of hidden unit activations $H$ with $\gamma H + \beta$ rather than simply the normalized $H$. The variables $\gamma$ and $\beta$ are learned parameters that allow the new variable to have any mean and standard deviation.

Then, one question arises: Why did we set the mean to 0, and then introduce a parameter that allows it to be set back to any arbitrary value $\beta$ again? The new parametrization can represent the same family of functions of the input as the old parametrization, but the new parametrization has different learning dynamics.

In the old parametrization, the mean of $H$ was determined by a complicated interaction between the parameters (weights) in the layers below $H$. So, if the model is slightly change, the result will be very different from the previous result, which is unpredictable a lot. And to find well-tuned model, we should consider copious amount of the parameters below $H$ and they should be interact well.

In the new parametrization, the mean of $\gamma H + \beta$ is determined solely by $\mathbf{\beta}$. Batch normalization makes each hidden unit reset the input’s distribution and tunes again with their own shift and scale parameters. The new parametrization is much easier to learn with gradient descent.

Where to put BN?

One question we have to answer is where we should put these batch normalization layers in practice? In a nut shell, both work, but it is still occasionally topic of debate. [5], [6], [7], [8], [9]

The classic way and suggested way by the original paper is to put normalization between neural network and non-linearity. For example, Andrew Ng also argues that it should be applied immediately before the non-linearity. And Yoshua Bengio’s book Deep Learning, §8.7.1 explains why BN should be applied before activation.

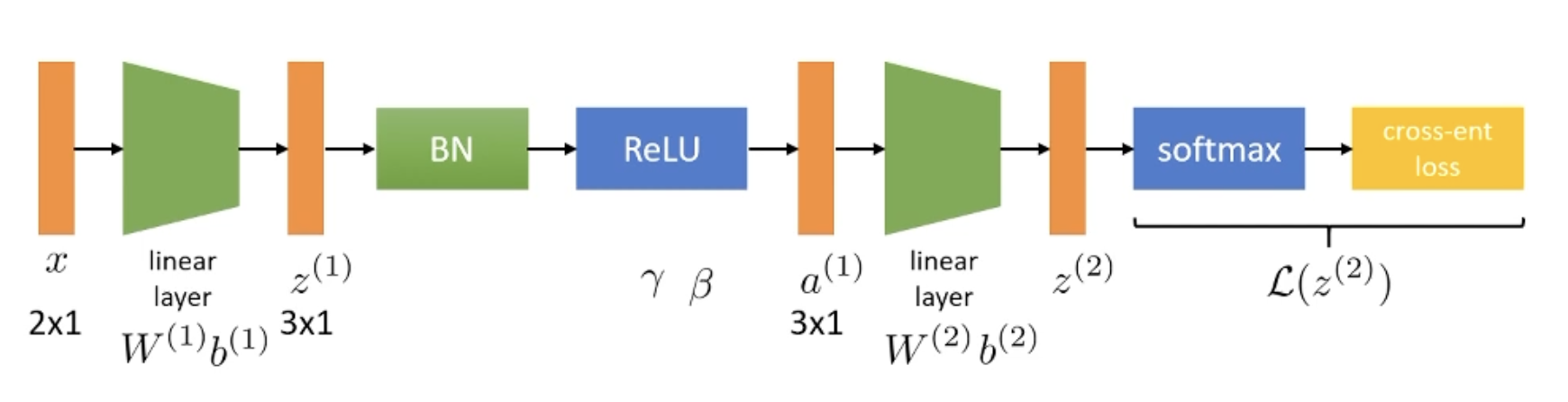
In contrast, François Chollet, for example, and some reports and experiments suggest that it is better to use batch normalization after the activation.

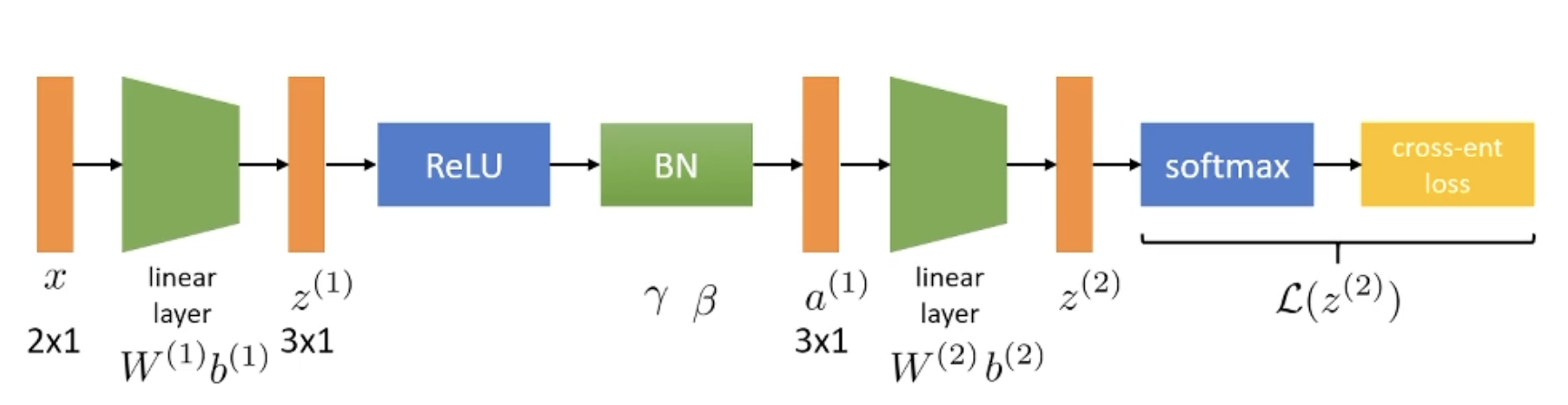
In short, I summarize some representative reasons of each contention:

• Before non-linearity
  
  • It normalizes the input to your activation function, so that you’re centered in the linear section of the activation function, such as sigmoid. [6]
    
  • BN after ReLU can be heavily skewed to the right. [7]
    
• After non-linearity
  
  • Internal covariate shift occurs when the distribution of the activations of a layer (input of the next layer) shifts significantly throughout training. To prevent internal covariate shift, the distribution of the inputs to a layer doesn’t change over time due to parameter updates from each batch. [6]
    
  • Some benchmarks show BN performing better after the activation layers. [8, 9]
    

At Test Time

At test time, we usually do not have a batch. That is, if the batch size is 1, we cannot normalize. So,

1. After training completes, compute the mean and variance on the entire training set and use it at test time.
2. Or we can do online averaging during training (if dataset is too big to compute the statistics in a batch mode). After training, we will have averaged batch mean and variance.

The algorithm proposed by the original paper uses the mean of batch means & variances that it calculated during training times at test time. Note that it multiplies $\frac{m}{m-1}$ to mean of batch variances to make it unbiased to the variance of data.

Backpropagation of BN

By drawing computational graph, we can derive backpropagation of BN easily. Consider

Note that loss function is denoted by $l$. Then,

\[\begin{align*} &\frac{\partial l}{\partial \widehat{x}_i} = \frac{\partial l}{\partial y_i} \cdot \gamma \\ &\frac{\partial l}{\partial \sigma^2_B} = \sum_{i=1}^m \frac{\partial l}{\partial \widehat{x}_i} \cdot (x_i - \mu_B) \cdot \frac{-1}{2} (\sigma^2_B + \epsilon)^{-3/2} \\ &\frac{\partial l}{\partial \mu_B} = (\sum_{i=1}^m \frac{\partial l}{\partial \widehat{x}_i} \cdot \frac{-1}{\sqrt{\sigma^2_B + \epsilon}}) + \frac{\partial l}{\partial \sigma^2_B} \cdot \frac{\sum_{i=1}^m -2 (x_i - \mu_B)}{m} \\ &\frac{\partial l}{\partial x_i} = \frac{\partial l}{\partial \widehat{x}_i} \cdot \frac{1}{\sqrt{\sigma^2_B + \epsilon}} + \frac{\partial l}{\partial \sigma^2_B} \cdot \frac{2(x_i - \mu_B)}{m} + \frac{\partial l}{\partial \mu_B} \cdot \frac{1}{m} \\ &\frac{\partial l}{\partial \gamma} = \sum_{i=1}^m \frac{\partial l}{\partial y_i} \cdot \widehat{x}_i \\ &\frac{\partial l}{\partial \beta} = \sum_{i=1}^m \frac{\partial l}{\partial y_i} \\ \end{align*}\]

Other Normalizations

Reference

[1] S. Oiffe and C. Szededy, Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, ICML 2015
[2] S. Santurkar et al., How Does Batch Normalization Help Optimization?, NeuRIPS 2018
[3] Quora, Is there a theory for why batch normalization has a regularizing effect?
[4] Stack Exchange, Why does batch normalization have learnable scale and shift?
[5] Stack Overflow, Where to apply batch normalization on standard CNNs
[6] Stack Overflow, Where do I call the BatchNormalization function in Keras?
[7] Stack Overflow, add Batch Normalization immediately before non-linearity or after in Keras?
[8] Github Issue, BN Questions (old)
[9] Github Issue, BatchNorm after ReLU