[Generative Model] CycleGAN

Introduction

Image-to-image translation is a class of vision and graphics problems where the goal is to learn the mapping between an input image and an output image using paired dataset. And it is usually based on conditional GAN (cGAN). However, a major drawback of cGANs is that we need to collect paired dataset \(\mathcal{D} = \{(\mathbf{x}_n, \mathbf{y}_n) \mid n = 1, 2, \cdots, N \}\), which is unavailable for many tasks. It is rather easy to collect two separated unpaired dataset \(\mathcal{D}_x \{ \mathbf{x}_n \mid n = 1, 2, \cdots, N \}\) and \(\mathcal{D}_y \{ \mathbf{y}_n \mid n = 1, 2, \cdots, N \}\), for example (taken from [2]) consider a set of daytime images, and that of night-time images; it would be easy to collect individual scenes for each dataset than a paired dataset in which exactly the same scene is recorded during the day and night.

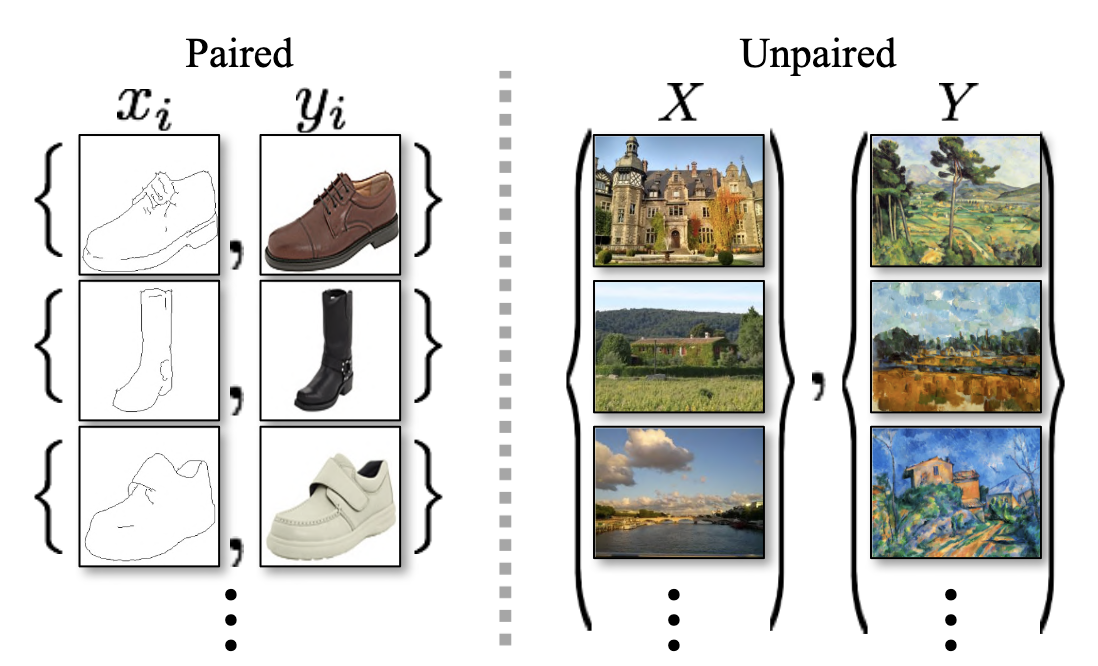
$\mathbf{Fig\ 1.}$ Paired v.s. Unpaired training data (source: Jun-Yan Zhu et al. ICCV 2017)

Cycle-Consistent GAN (CycleGAN) proposed by Jun-Yan Zhu et al. ICCV 2017 can learn to translate between domains of image without any need of paired dataset. Instead of supervised the model through the paired connection, the authors introduced the concept of cycle consistency to the model: if the data $\mathbf{x}$ is translated to data in another domain $\mathbf{y}$, then $\mathbf{y}$ should return at the original data $\mathbf{x}$ if we translate it back.

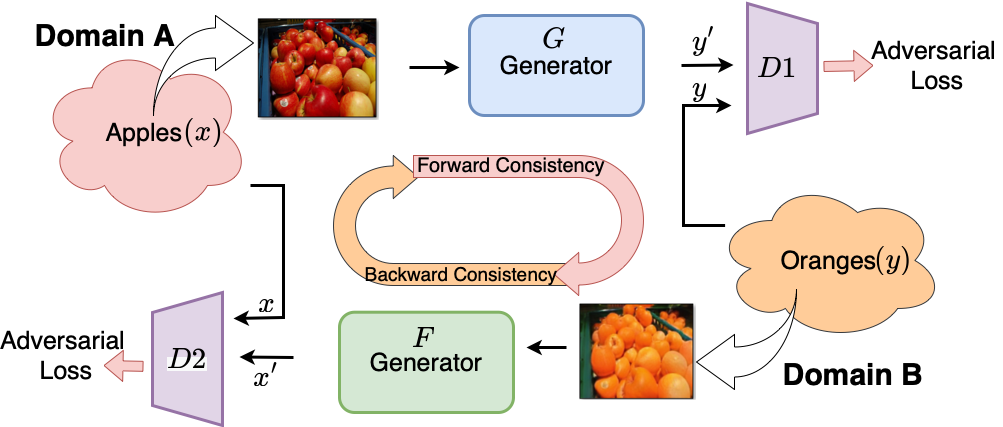
$\mathbf{Fig\ 2.}$ The end-to-end training pipeline of CycleGAN to achieve unpaired image translation (source: Shivam Chandhok)

CycleGAN

There’s nothing more than loss function formulation to understand cycleGAN.

Adversarial loss

First of all, recall that the loss in the vanilla GAN is written as for generator $G: X \to Y$ where the data is sampled from $p_{\text{data}}(\mathbf{x})$ and discriminator $D_Y$:

\[\begin{aligned} \mathcal{L}_{\text{GAN}} (G, D_Y, X, Y) = \mathbb{E}_{y \sim p_{\text{data}} (\mathbf{y})} \left[ \text{ log } D_Y (\mathbf{y}) \right] + \mathbb{E}_{x \sim p_{\text{data}}} \left[ \text{ log } (1 - D_Y (G(\mathbf{x})))\right] \end{aligned}\]

This loss forces GAN to generate images $G( \mathbf{x})$ that is indistinguishable from domain $Y$, and $D_Y$ will make an effort to distinguish between them. And in analogous way we define $\mathcal{L}_{\text{GAN}} (F, D_X, Y, X)$ too. We will referred to these as adversarial losses.

Cycle consistency loss

But employing adversarial losses only for domain translation may go wrong, since the adversarial loss only ensures the quality of sample at the distribution level. Let’s think about an example:

$\mathbf{Fig\ 3.}$ Image translation from zebra domain to horse domain (source: Shivam Chandhok)

It seems that an image that belongs to the zebra distribution of images is translated into an image in the horse distribution well. At least in distribution perspective. But can we say that the translated image is desirable? To guarantee consistency of images at the sample level, cycleGAN introduces an additional constraint called cycle consitency that constraints two mappings are invertible, i.e. $F(G(\mathbf{x})) \approx \mathbf{x}$ (forward cycle consistency) and $G(F(\mathbf{y})) \approx \mathbf{y}$ (backward cycle consistency).

$\mathbf{Fig\ 4.}$ Forward cycle consistency (source: Jun-Yan Zhu et al. ICCV 2017)

And we encourage this invertibility in terms of loss fuction while training:

\[\begin{aligned} \mathcal{L}_{\text{cycle}} (G, F) = \mathbb{E}_{\mathbf{x} \sim p_{\text{data}} (\mathbf{x})} \left[ \| F(G(\mathbf{x})) - \mathbf{x} \|_1 \right] + \mathbb{E}_{\mathbf{y} \sim p_{\text{data}} (\mathbf{y})} \left[ \| G(F(\mathbf{y})) - \mathbf{y} \|_1 \right] \end{aligned}\]

which is called cycle consistency loss.

Identity loss (Optional)

In the experiment of painting $\to$ photo, the authors found that it is helpful to introduce an additional loss to encourage the mapping to preserve color composition between the input and output. Inspired by Taigman et al.,

\[\begin{aligned} \mathcal{L}_{\text{identity}} (G, F) = \mathbb{E}_{\mathbf{y} \sim p_{\text{data}} (\mathbf{y})} \left[ \| G(\mathbf{y}) - \mathbf{y} \|_1 \right] + \mathbb{E}_{\mathbf{x} \sim p_{\text{data}} (\mathbf{x})} \left[ \| F(\mathbf{x}) - \mathbf{x} \|_1 \right] \end{aligned}\]

which regularizes the generator to be near an identity mapping when real samples of the target domain are provided as the input to the generator. We will referred to this loss as identity loss.

$\mathbf{Fig\ 5.}$ Effect of $\mathcal{L}_{\text{identity}}$ (source: Jun-Yan Zhu et al. ICCV 2017)

Total loss

These losses are combined into a single full objective:

\[\begin{aligned} \mathcal{L} = \mathcal{L}_{\text{GAN}}(G, D_Y, X, Y) + \mathcal{L}_{\text{GAN}}(F, D_X, Y, X) + \lambda \mathcal{L}_{\text{cycle}} (G, F) \end{aligned}\]

Or, with identity loss

\[\begin{aligned} \mathcal{L} = \mathcal{L}_{\text{GAN}}(G, D_Y, X, Y) + \mathcal{L}_{\text{GAN}}(F, D_X, Y, X) + \lambda_1 \mathcal{L}_{\text{cycle}} (G, F) + \lambda_2 \mathcal{L}_{\text{identity}} (G, F) \end{aligned}\]

The following figure illustrates the cycleGAN training scheme:

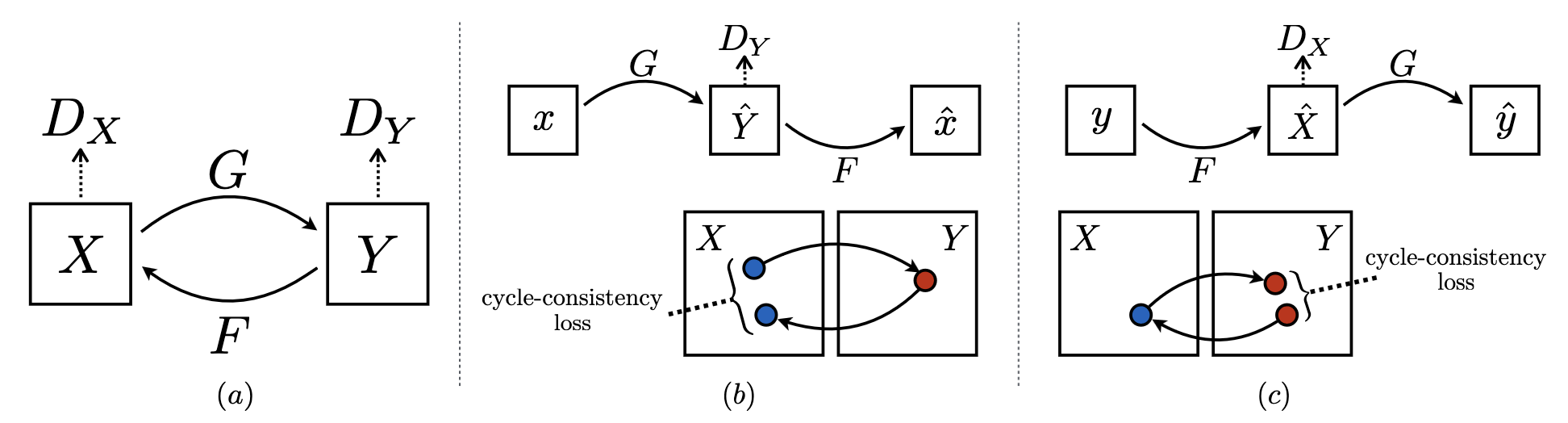
$\mathbf{Fig\ 6.}$ Illustration of the CycleGAN training scheme (source: Jun-Yan Zhu et al. ICCV 2017)

Summary

In summary,

1. Goal: learn mapping functions between two domains $X$ and $Y$ with only unpaired dataset for each domain $\mathcal{D}_x = \{ \mathbf{x}_i \in X \mid i = 1, 2, \dots, N \}$ and $\mathcal{D}_y = \{ \mathbf{y}_j \in Y \mid j = 1, 2, \dots, M \}$
2. Our model:
   • two mappings (generator) from one domain to another $G: X \to Y$ and $F: Y \to X$
   • two adversarial discriminators for each domain $D_X$ and $D_Y$
     • $D_X$ distinguishes between real image $\mathbf{x} \in \mathcal{D}_x$ and translated images $F (\mathbf{y})$
     • $D_Y$ distinguishes between real image $\mathbf{y} \in \mathcal{D}_y$ and translated images $G (\mathbf{x})$
3. Objectives
   • adversarial losses
   • cycle consistency loss
   • identity loss (optional)

Hence, cycleGAN can be employed in various image translation tasks such as style transfer. And despite learning with unpaired dataset, it performs comparatively well with some models including Pix2Pix trained on a paired dataset.

$\mathbf{Fig\ 7.}$ Examples of generated samples by CycleGAN (source: Jun-Yan Zhu et al. ICCV 2017)

But obviously there are limitations for some tasks that require geometric changes: CycleGAN can only make minimal changes to the input due to cyclic consistency. And the authors observed that some failure cases are caused by the distribution characteristics of the training datasets. Here are examples.

$\mathbf{Fig\ 8.}$ Failure examples of generated samples by CycleGAN (source: Jun-Yan Zhu et al. ICCV 2017)

Reference

[1] Zhu, Jun-Yan, et al. “Unpaired image-to-image translation using cycle-consistent adversarial networks.” Proceedings of the IEEE international conference on computer vision. 2017..
[2] Kevin P. Murphy, Probabilistic Machine Learning: Advanced Topics, MIT Press 2022.
[3] Shivam Chandhok, CycleGAN: Unpaired Image-to-Image Translation (Part 1)