[Generative Model] Conditioned Diffusion Models

Diffusion models have exhibited superior performance compared to previous state-of-the-art generative models, spurring researchers to explore their remarkable generative capabilities across a spectrum of downstream tasks. Notably, conditional generation using pretrained diffusion models in a zero-shot or few-shot fashion has emerged as a focal point of research. Consequently, conditional diffusion models leveraging diverse conditioning inputs, including text, class labels, degraded images, segmentation maps, landmarks, hand-drawn sketches, and more, have been introduced. This post provides a concise overview of select works in this domain.

Zero-shot Applications

The training-free methods leverage various innovative techniques to achieve condition generation without additional training for certain tasks, exploiting the unique iterative denoising process inherent to diffusion models.

SDEdit: Guided Image Synthesis & Editing

Stochastic differential editing (SDEdit) facilitates image generation and editing of diffusion models through user interaction, devoid of task-specific training or loss functions. Any form of manipulating RGB pixels, including stroke painting or an image with stroke edits, can be injected to the SDE-based generative models, yielding realistic and faithful images from guides with various levels of fidelity.

$\mathbf{Fig\ 1.}$ SDEdit can generate realistic, faithful and diverse images for a given stroke input drawn by human (Meng et al. 2022)

The fundamental insight behind SDEdit is to hijack the generative process of SDE-based generative models by introducing an appropriate level of noise to smooth out undesirable artifacts and distortions in user guidance input, while retaining the overarching structure. Subsequently, the reverse process of diffusion is executed to eliminate the noise, yielding a denoised result that is both realistic and faithful to the initial user guidance input.

$\mathbf{Fig\ 2.}$ Synthesizing images from strokes with SDEdit (Meng et al. 2022)

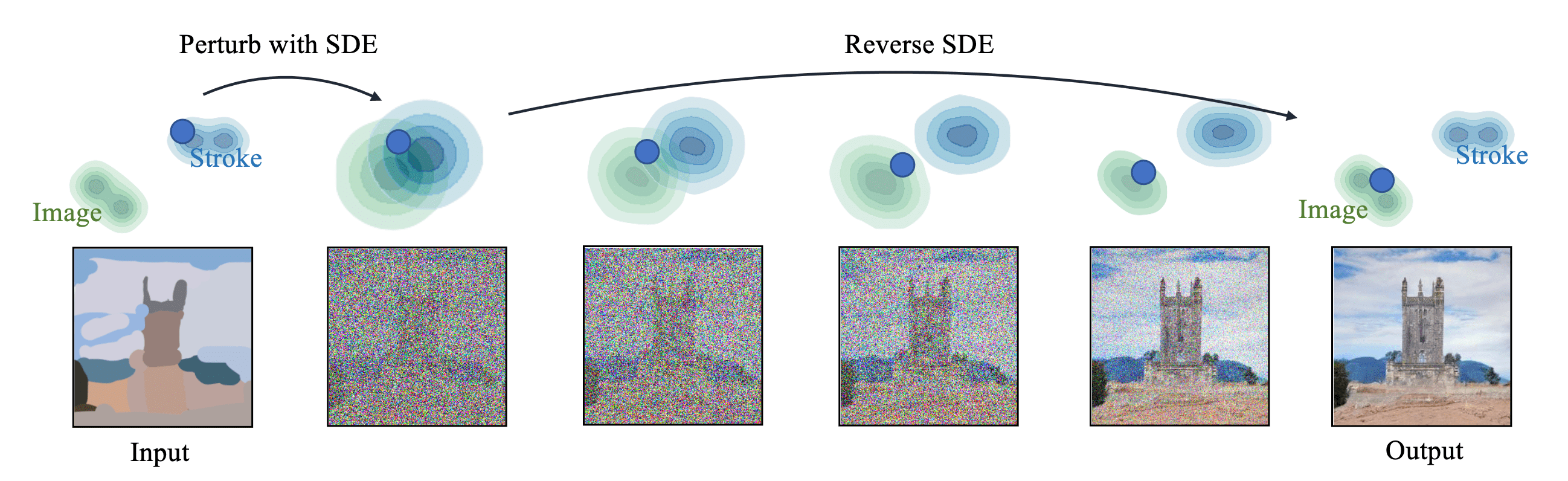
Formally, consider the following perturbing forward process of SDE-based generative models for time interval $t \in [0, 1]$:

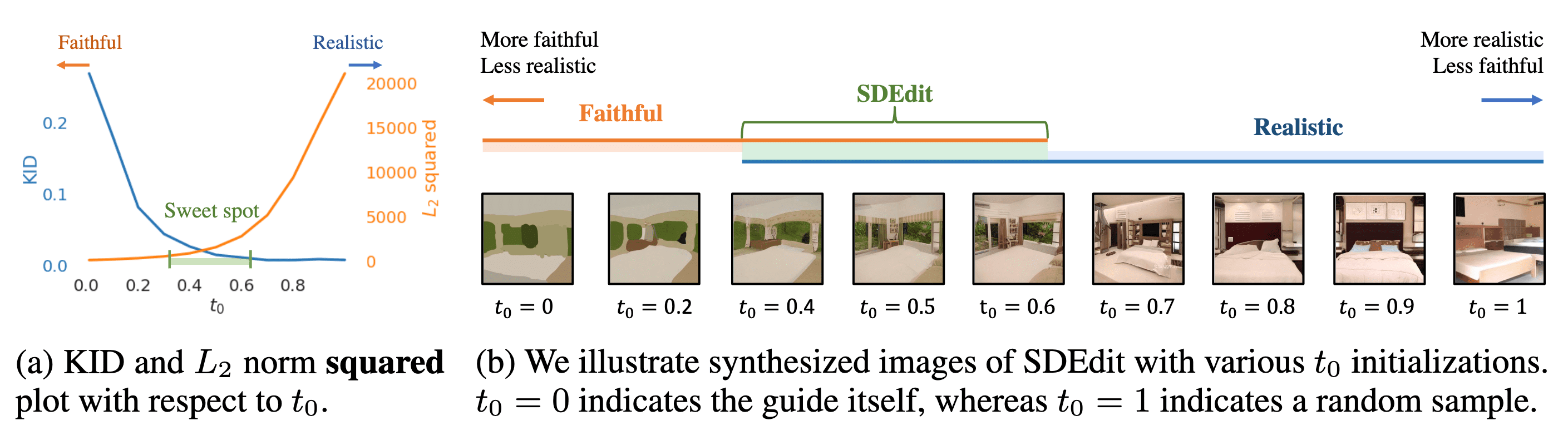
\[\mathbf{x}(t) = \alpha(t) \mathbf{x}(0) + \sigma(t) \mathbf{z} \quad \text{ where } \quad \mathbf{x}(0) \sim p_{\mathrm{data}}, \mathbf{z} \sim \mathcal{N} (\mathbf{0}, \mathbf{I})\]

Note that we generally set $\alpha (t) \to 0$ and $\sigma(t) \to 1$ as $t \to 1$. For instance, DDPM adopts $\alpha (t) = \sqrt{\bar{\alpha}_t}$ and $\sigma (t) = \sqrt{1 - \bar{\alpha}_t}$. Given a user guidance image $\mathbf{x}^{(g)}$, it samples $\mathbf{x}^{(g)} (t_0) \sim \mathcal{N}(\mathbf{x}^{(g)}, \sigma^2 (t_0) \mathbf{I})$ and obtain the denoised generated output $\mathbf{x} (0) = \mathrm{SDEdit} (\mathbf{x}^{(g)}; t_0, \theta)$ by iterating the reverse SDE. The key hyperparameter for SDEdit is $t_0 \in (0, 1)$, denoting the initiation time for the image synthesis procedure in the reverse SDE, and also indicating the degree of forward processsing. Indeed, it determines the degree of realism-faithfulness trade-off. In practice, the authors found that $t_0 \in [0.3, 0.6]$ works well.

$\mathbf{Fig\ 3.}$ Trade-off between faithfulness and realism for SDEdit. (Meng et al. 2022)

RePaint: Inpainting with DDPM

RePaint, DDPM-based inpainting algorithm proposed by Lugmayr et al. 2022 has demonstrated that unconditionally pre-trained image diffusion models excel at inpainting task without any additional training and tuning, effectively filling regions of the missing forground while preserving the given background.

$\mathbf{Fig\ 4.}$ Visualization of samples generated from RePaint (Lugmayr et al. 2022)

Formally, the goal of inpainting is to predict missing pixels $m \odot \mathbf{x}$ of the ground truth image $\mathbf{x}$ using a mask region $m$ as a condition, while preserving the known pixels as $(1 - m) \odot \mathbf{x}$. And RePaint combines denoised foreground images to be filled, and noisy background to be fixed images at each iteration of the reverse process:

1. Sampling foreground image $\mathbf{x}^{\mathrm{unknown}}$
   Starting from $\mathbf{x}_T$, at each timestep $t$, denoise $\mathbf{x}_t$ one step with reverse process, yielding $\mathbf{x}_{t-1}^{\mathrm{unknown}}$. $$ \mathbf{x}_{t-1}^{\mathrm{unknown}} \sim \mathcal{N} (\mu_\theta (\mathbf{x}_t, t), \Sigma_{\theta} (\mathbf{x}_t, t)) $$
2. Sampling background image $\mathbf{x}^{\mathrm{known}}$
   Perturb the input background image $\mathbf{x}_0$ via forward process with a noise scale of the timestep $t - 1$, yielding $\mathbf{x}_{t-1}^{\mathrm{known}}$. $$ \mathbf{x}_{t-1}^{\mathrm{known}} \sim \mathcal{N} (\sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t) \mathbf{I}) $$
3. Inpainting
   Combine $\mathbf{x}_{t-1}^{\mathrm{unknown}}$ and $\mathbf{x}_{t-1}^{\mathrm{known}}$ using the background mask $m$, yielding $\mathbf{x}_{t-1}$: $$ \mathbf{x}_{t-1} = m \odot \mathbf{x}_{t-1}^{\mathrm{known}} + (1-m) \odot \mathbf{x}_{t-1}^{\mathrm{unknown}} $$
   
   

   
   

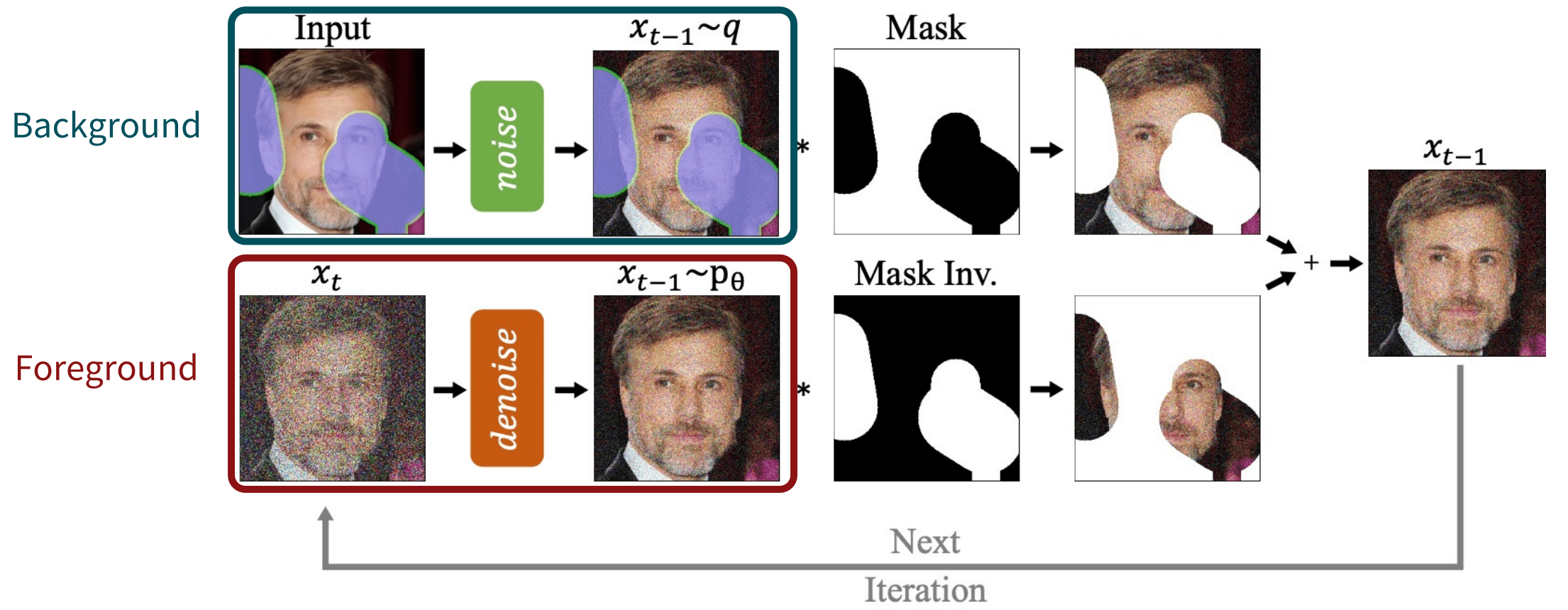
   $\mathbf{Fig\ 5.}$ Overview of sampling step of RePaint (Lugmayr et al. 2022)

4. Resampling
   The sampling of the background pixels, $\mathbf{x}^{\mathrm{known}}$, is performed independently of the generated parts of the image, which can result in disharmony. To address the semantic disparity between these samples, RePaint diffuses the output $\mathbf{x}_{t−1}$ back to $\mathbf{x}_t$ with $$ q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}( \mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}) $$ and resamples $\mathbf{x}_{t-1}$ again. Qualitatively, additional resampling steps lead to more harmonized images.
   
   

   
   

   $\mathbf{Fig\ 6.}$ The effect of applying $n$ sampling steps, where $n = 2$ is the DDPM with $1$ resampling (Lugmayr et al. 2022)
   
   

The following pseudo-code summarizes the pipeline of RePaint algorithm:

$\mathbf{Fig\ 7.}$ Pseudo-code of RePaint algorithm (Lugmayr et al. 2022)

Few-shot Adapations

Training-required methods can achieve robust control generation capabilities through fine-tuning with data pairs. One of the most prominent applications of these methods is the text-to-image task, which can be accomplished with few-shot fine-tuning.

Text-to-Image Few-shot Personalization

Adapting Stable Diffusion to a particular style is typically done by prompt engineering, or by fine-tuning the U-Net on a set of target style images, well-exemplified by Textual Inversion and DreamBooth.

Textual Inversion (TI)

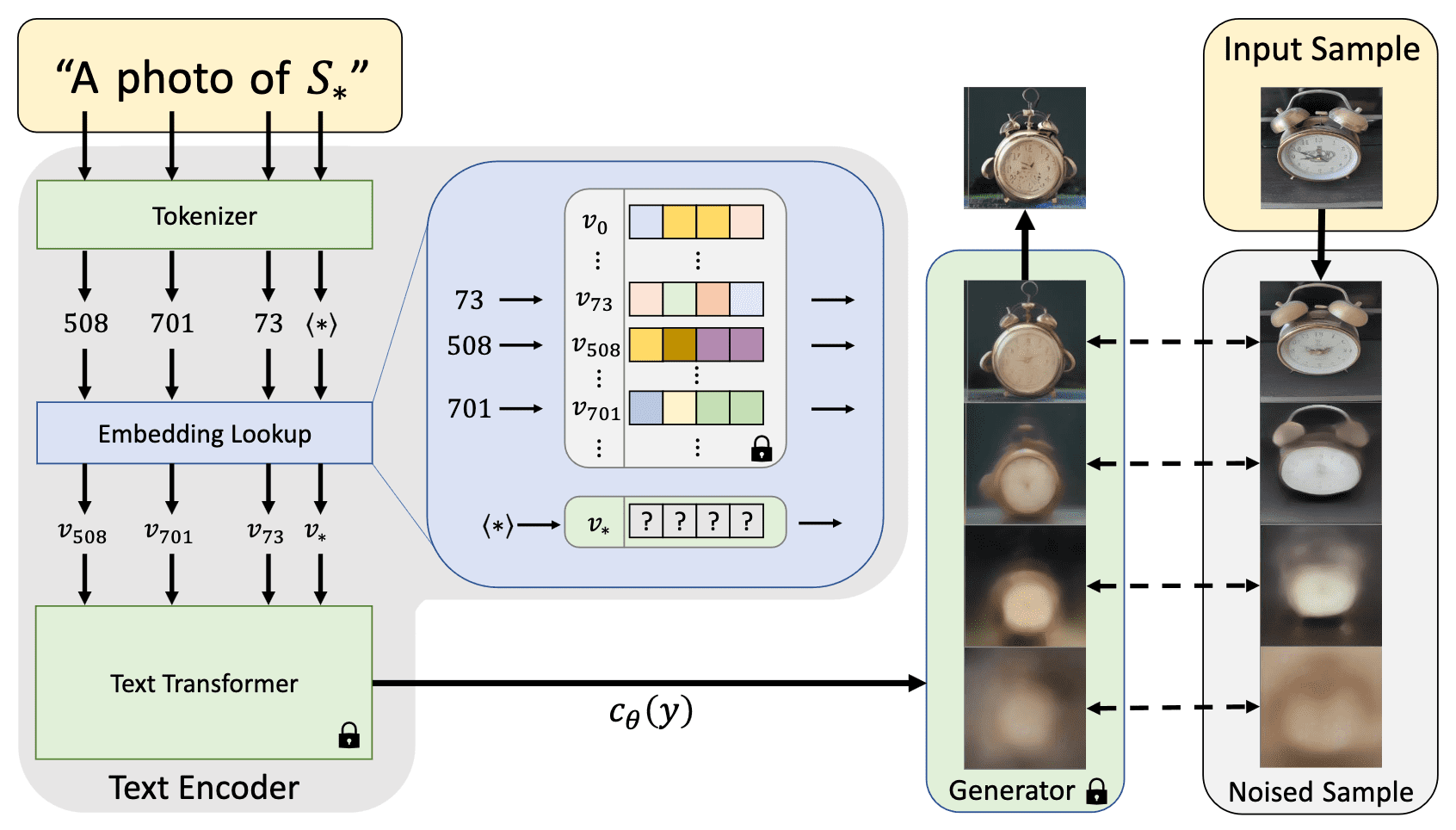
Instead of fine-tuning the diffusion model, a natural way to personalize the generated outputs with exemplar images is prompt engineering; to describe the desired style in the textual prompt. Textual Inversion (TI) introduces a new way of prompt engineering, by way of learning new “words” from a small set of exemplar images.

To inject the specific concept or particular style of exemplar images within textual embedding space of pre-trained text-to-image models, Textual Inversion inverts the new, specific concept of exemplar images by optimizing the embedding vector \(\mathbf{v}_*\) to find new tokens of pseudo-word \(S_*\) that represent specific concepts of given images.

$\mathbf{Fig\ 8.}$ Textual Inversion learns to generate specific concepts by describing them using new "words" in the embedding space of pre-trained diffusion. (Gal et al. 2023)

1. Text Embedding
   Each word or sub-word in an input string is converted to a token $n \in \mathbb{N}$, which corresponds to an index in some pre-defined dictionary. Each token is then linked to corresponding unique embedding vector $v_n$ that can be retrieved via index lookup. The embedding vectors are transformed into a single conditioning code $c_\theta (y)$ by the text encoder $c_\theta$, which subsequently guides the generative model.
2. Textual Inversion
   To find these new embeddings, a small set of images (typically 3-5) depicting the target concept across multiple settings, such as varied backgrounds or poses, is used. The embedding vector $v_*$ of $S_*$ is directly optimized by minimizing the LDM loss: $$ \mathbf{v}_* = \underset{\mathbf{v}}{\arg \min} \; \mathbb{E}_{\mathbf{z} \sim \mathcal{\varepsilon} (\mathbf{x}), y, \epsilon \sim \mathcal{N}(0, 1), t} [\Vert \epsilon - \epsilon_\theta (\mathbf{z}_t, t, c_\theta (y)) \Vert_2^2] $$ while freezing both $c_\theta$ and $\epsilon_\theta$.

$\mathbf{Fig\ 9.}$ Outline of the text-embedding and inversion process (Gal et al. 2023)

However, akin to the prompt engineering technique, this approach is limited by text embedding’s capacity to capture the style characteristics and the expressiveness of the frozen diffusion model to mimic the visual appearance of subjects in a given reference set, and synthesize novel renditions of the same subjects in different contexts.

DreamBooth

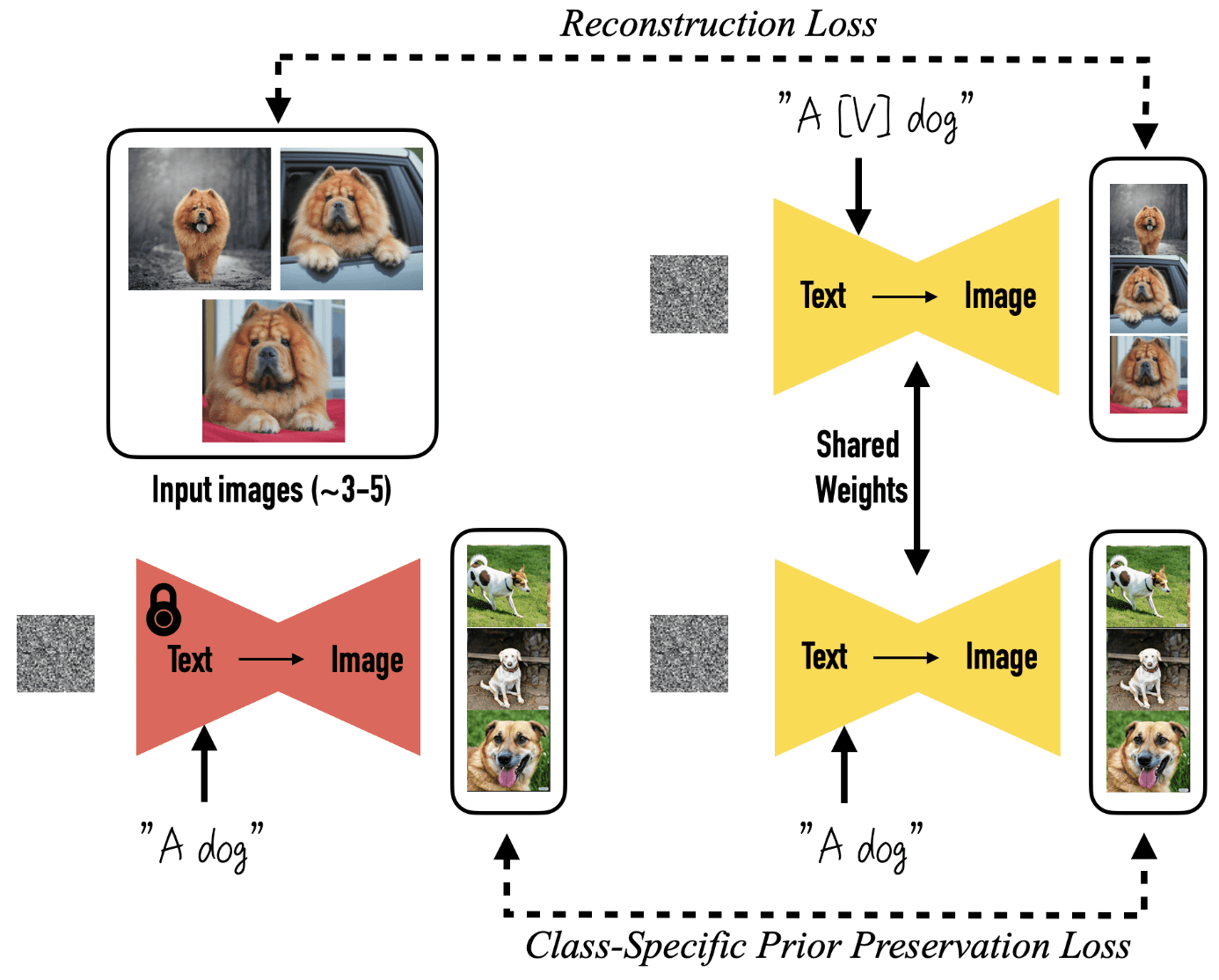
Only with 3~5 exemplar images, one can fine-tune text-to-image diffusion to specific objects or people, thereby expanding language-vision dictionary of pre-trained model, using a method called DreamBooth of Ruiz et al. 2023. Typically, it requires about 1000 iterations with 3 ~ 5 reference images.

Given a few images of a subject, DreamBooth aims to implant the subject into the output domain of the model such that it can be synthesized with a unique identifier $[\mathrm{V}]$. Text-to-image diffusion model is fine-tuned with the input images paired with a text prompt containing a unique identifier and the name of the class the subject belongs to, e.g., "A [V] dog". In parallel, to prevent language drift that causes the model to associate the class name with the specific instance, a class-specific prior preservation loss encourages the model to generate diverse instances belong to the subject’s class using the class name in the text prompt.

$\mathbf{Fig\ 10.}$ With just a few images of a subject, DreamBooth can generate images of the subject in different contexts, using the guidance of a text prompt. (Ruiz et al. 2023)

1. Personalization Prompts
   To bypass the overhead of writing detailed image descriptions, for a given image set, it labels all input images of the subject "a [identifier] [class noun]". The class descriptor aids in tethering the class-prior to the unique subject of exemplar images. In case of identifier, to prevent entangling with other words and class descriptor, an identifier should have weak prior in both the language model and the diffusion model.
   
   To find such tokens, the authors look-up rare-token $f( \hat{\mathbf{V}} )$, where $f$ is the tokenizer and obtain a sequence of characters $\hat{\mathbf{V}}$ by de-tokenizing $f( \hat{\mathbf{V}} )$.
2. Class-specific Prior Preservation Loss
   There are two major challenges for fine-tuning text-to-image models:
   • Language drift
     Fine-tunining for a specific task progressively extinguishes syntactic and semantic knowledge of the language of pre-trained model.
   • Reduced output diversity
     The model must generate the subject in innovative viewpoints, poses, and articulations. However, fine-tuning might diminish the variability in the output poses and perspectives of the subject, solidified in the limited few-shot views.
   To retain the pre-trained prior space and generate diverse images of the class prior, DreamBooth supervises the model with its own generated samples $\mathbf{x}_{\mathrm{pr}} = \hat{\mathbf{x}} (\mathbf{z}_{t_1}, \mathbf{c}_{\mathrm{pr}})$ from the frozen pre-trained diffusion model $\hat{\mathbf{x}}$ with random initial noise $\mathbf{z}_{t_1} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ and conditioning vector $\mathbf{c}_{\mathrm{pr}} := \Gamma(f (\textrm{a [class noun]}))$. Then, it is fine-tuned with the following loss function: $$ \mathbb{E}_{\mathbf{x}, \mathbf{c}, \boldsymbol{\epsilon}, \boldsymbol{\epsilon}^\prime, t} [w_t \Vert \hat{\mathbf{x}}_\theta (\alpha_t \mathbf{x} + \sigma_t \boldsymbol{\epsilon}, \mathbf{c}) − \mathbf{x} \Vert_2^2 + \lambda w_{t^\prime} \Vert \hat{\mathbf{x}}_\theta (\alpha_{t^\prime} \mathbf{x}_{\mathrm{pr}} + \sigma_{t^\prime} \boldsymbol{\epsilon}^\prime, \mathbf{c}_{\mathrm{pr}}) − \mathbf{x}_{\mathrm{pr}} \Vert_2^2] $$ where the first term is the second term is the prior-preservation term that supervises the model with its own generated images, and $\lambda$ controls for the relative weight of this term.

$\mathbf{Fig\ 11.}$ Outline of DreamBooth fine-tuning (Ruiz et al. 2023)

ControlNet: Conditional Control to Text-to-Image Diffusions

Text-to-image models often lack precise control over the spatial composition of images, and to accurately express complex layouts, poses, shapes and forms is challenging via text prompts alone. Zhang et al. 2023 proposed ControlNet, which allows for efficient fine-tuning of an unconditionally trained image diffusion model for both image- and text-conditioned scenarios via a relatively smaller set of input-output pairs ($< 50\mathrm{k}$).

$\mathbf{Fig\ 12.}$ Controlling Stable Diffusion with learned conditions. (Zhang et al. 2023)

ControlNet is an end-to-end neural network architecture that attaches to frozen, large pretrained text-to-image diffusion models, enabling conditional controls for these extensive models. By integrating with the large model, ControlNet injects additional conditions into the blocks of a neural network. Specifically, consider a trained neural block $\mathcal{F}(\cdot; \Theta)$ with parameters $\Theta$, which transforms an input feature map $\mathbf{x}$, into another feature map $\mathbf{y}$:

\[\mathbf{y} = \mathcal{F}(\mathbf{x}; \Theta)\]

To preserve the quality and capabilities of the large model, ControlNet locks $\Theta$, but instead clones this neural block to a trainable copy with parameters $\Theta_\mathrm{c}$, which takes an external conditioning vector $\mathbf{c}$ as input. This trainable copy is connected to the locked model with two zero convolution layers $\mathcal{Z}(\cdot; \cdot)$, $1 \times 1$ convolution layer with both weight $\mathbf{w}$ and bias $\mathbf{b}$ initialized to $\mathbf{0}$:

\[\mathcal{Z}(\mathbf{x}; \mathbf{w}, \mathbf{b}) = \mathbf{w} \cdot \mathbf{x} + \mathbf{b}\]

The complete ControlNet then computes:

\[\mathbf{y}_\mathrm{c} = \mathcal{F}(\mathbf{x}; \Theta) + \mathcal{Z}(\mathcal{F}(\mathbf{x} + \mathcal{Z}(\mathbf{c}; \mathbf{w}_1, \mathbf{b}_1); \Theta_\mathrm{c}); \mathbf{w}_2, \mathbf{b}_2)\]

$\mathbf{Fig\ 13.}$ ControlNet block (Zhang et al. 2023)

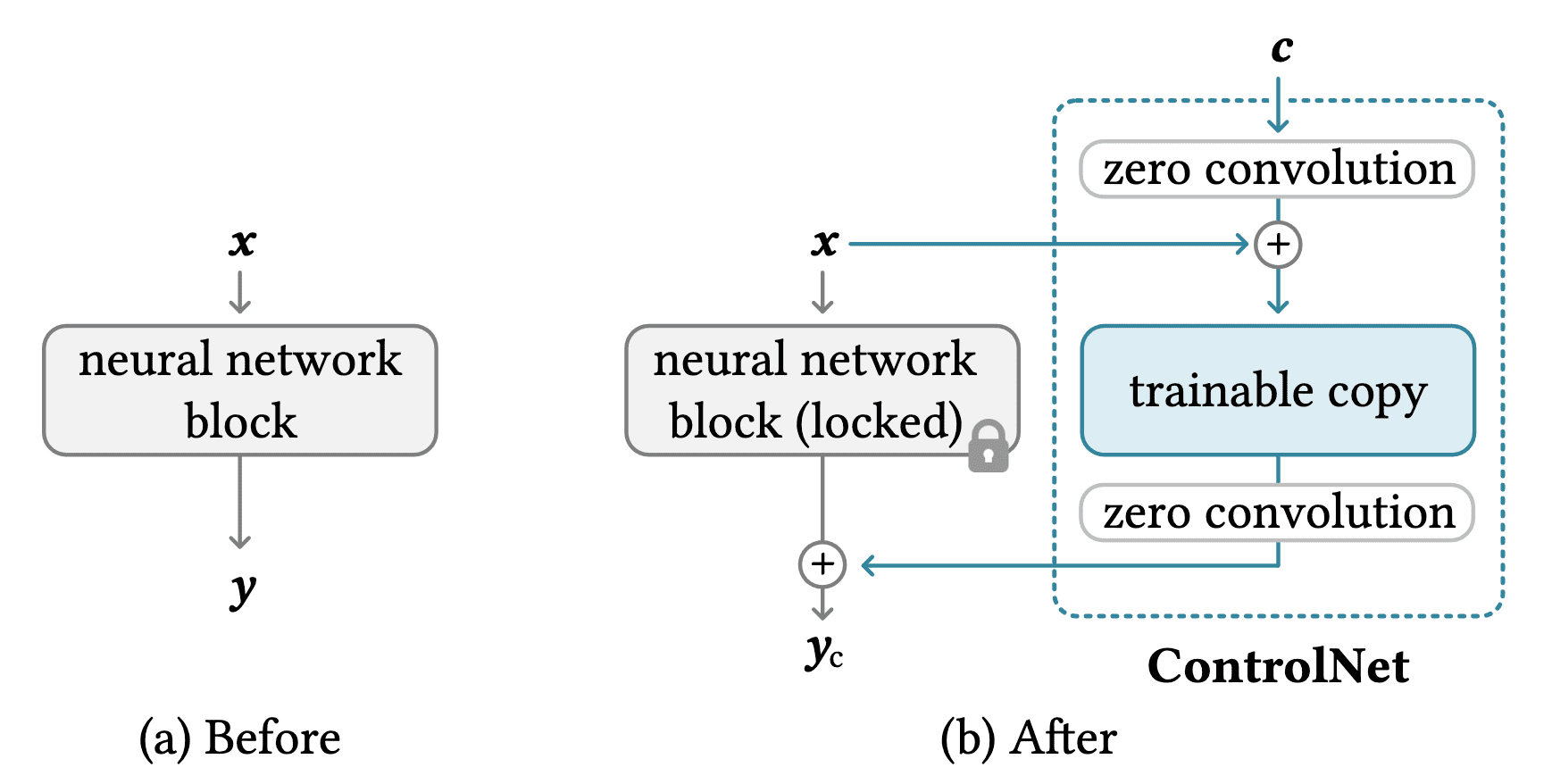
Note that $\mathbf{y}_\mathrm{c} = \mathbf{y}$ and $\frac{\partial \mathcal{Z}}{\partial \mathbf{I}} = \mathbf{0}$ as zero convolution initializes its parameters to zero. That means ControlNet begins with the state identical to the unconditional case, without adapting the conditional information initially, and gradually introduces the conditional information. This architecture ensures that harmful noise is not introduced into the deep features of the large diffusion model at the beginning of fine-tuning, enabling the model to retain the capabilities of the large, pretrained model and allowing it to serve as a robust backbone for further learning.

This modification can be further extended to the entire text-to-image diffusion model by adapting each neural network block with zero convolutions:

• For the encoder of the conditional image, clone the pre-trained U-Net parameters while permitting them to be updated during fine-tuning.
• Integrate the encoded conditional image information with the noisy image using zero convolution.

Given an input image \(\mathbf{z}_0\) and corresponding noisy image \(\mathbf{z}_t\), the diffusion model $\epsilon_\theta$ of ControlNet is fine-tuned by optimizing the following loss given text prompts \(\mathbf{c}_\mathrm{t}\) and task-specific condition \(\mathbf{c}_\mathrm{f}\):

\[\mathcal{L} = \mathbb{E}_{\mathbf{z}_0, t, \mathbf{c}_\mathrm{t}, \mathbf{c}_\mathrm{f}, \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I})} [\Vert \epsilon - \epsilon_\theta (\mathbf{z}_t, t, \mathbf{c}_\mathrm{t}, \mathbf{c}_\mathrm{f}) \Vert_2^2 ]\]

$\mathbf{Fig\ 14.}$ Overview of ControlNet (Zhang et al. 2023)

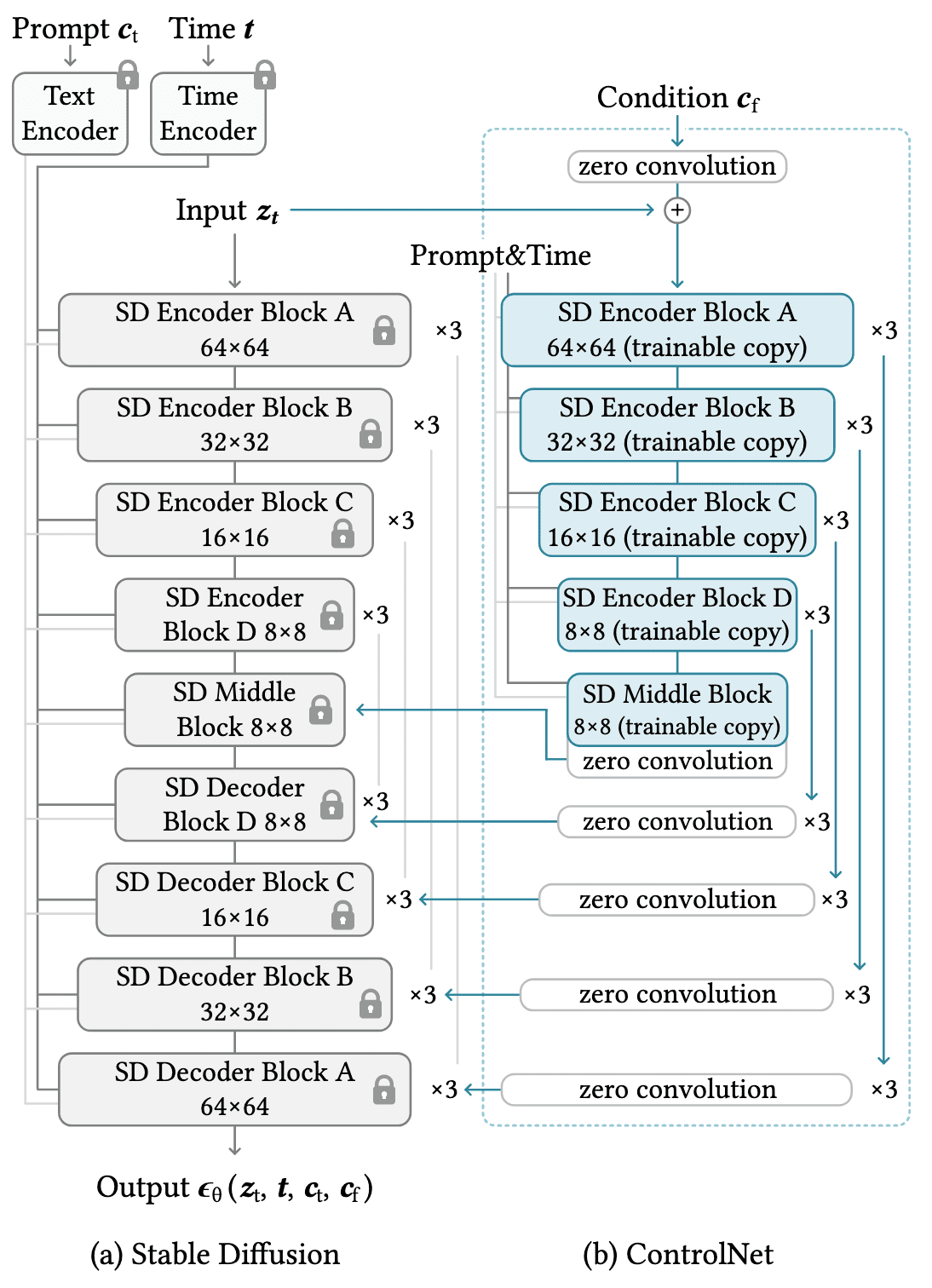
Experimentally, ControlNet has demonstrated robust interpretation of content semantics in various input conditioning images, such as edge maps, segmentation maps, depth maps, etc.

$\mathbf{Fig\ 15.}$ Controlling Stable Diffusion with various conditions without prompts. (Zhang et al. 2023)

References

[1] Meng et al., SDEdit: Guided Image Synthesis and Editing with Stochastic Differential Equations, ICLR 2022.
[2] Lugmayr et al., RePaint: Inpainting using Denoising Diffusion Probabilistic Models, CVPR 2022.
[3] Ruiz et al., DreamBooth: Fine Tuning Text-to-Image Diffusion Models for Subject-Driven Generation, CVPR 2023.
[4] Gal et al., An Image is Worth One Word: Personalizing Text-to-Image Generation using Textual Inversion, ICLR 2023.
[5] Zhang et al., Adding Conditional Control to Text-to-Image Diffusion Models, ICCV 2023.
[6] Yu et al., FreeDoM: Training-Free Energy-Guided Conditional Diffusion Model ICCV 2023