[Measure Theory] Construction of measures
The goal of this post is to construct measures. Intuitively, we want the measure $m$ of an open interval on real line $\mathbb{R}$ to be the length of the interval, i.e. $m((a, b)) = b - a$. Then from the requirement of measures,
\[\begin{aligned} m \left( \bigcup_{i=1}^\infty (a_i, b_i) \right) = \sum_{i=1}^\infty (b_i - a_i) \end{aligned}\]From the fact that every open subset of $\mathbb{R}$ is the countable union of disjoint open interval, for arbitrary subset $E \subset \mathbb{R}$ it is reasonable to assign a measure to $E$ as:
\[\begin{aligned} m (E) = \text{inf } \{m (G) \mid G \text{ is open}, E \subset G \}. \end{aligned}\]However the problem is that $m$ is not a measure on the $\sigma$-algebra consisting of all subsets of $\mathbb{R}$.
For example, we will construct a well-known counterexample, called Vitali set to see that $\sigma$-addivity is not always satisfied on the $\sigma$-algebra consisting of all subsets of $\mathbb{R}$, which proves that $m$ is not a measure. Let’s define an equivalence relation $\sim$ on $[0, 1]$ $x \sim y$: if $x - y \in \mathbb{Q}$. And select an element out of this equivalent class and denote that collection as $A$; $A \subset [0, 1]$. We will prove that $A$ is non-measurable with respect to $m$.
Notice that
since $q \in [-1, 1]$ and $A \subset [0, 1]$. And note that this union is countable union since $q \in \mathbb{Q}$ where $\mathbb{Q}$ is countable set, and for different $q$, $A + q$ are disjoint with each other. 2Suppose that our $m$ above is a measure on a $\sigma$-algebra containing $A + q$ for all $q \in [-1, 1] \cap \mathbb{Q}$. Then, from $\sigma$-additivity and discussion above,
\[\begin{aligned} 1 \leq m \left( \bigcup_{q \in [-1, 1] \bigcap \mathbb{Q}} (A + q) \right) = \sum_{q \in [-1, 1] \bigcap \mathbb{Q}} m (A + q) \leq 3 \end{aligned}\]In addition, since $A + q$ is just a translation of collection $A$ by $q$, $\sum_{q \in [-1, 1] \bigcap \mathbb{Q}} m (A + q) = \sum_{q \in [-1, 1] \bigcap \mathbb{Q}} m (A)$ and thus
\[\begin{aligned} 1 \leq \sum_{q \in [-1, 1] \bigcap \mathbb{Q}} m (A) \leq 3 \end{aligned}\]But it is a contradiction; since $\sum_{q \in [-1, 1] \bigcap \mathbb{Q}} m (A)$ is bounded by right-hand side inequality, thus $m (A)$ must be $0$ but it can’t due to left-hand side inequality. Hence $m$ can’t be a measure on $\sigma$-algebra consisting of all subsets of $\mathbb{R}$.
We will resolve this issue by considering a strictly smaller $\sigma$-algebra denoted by $\mathcal{L}$. And this $\sigma$-algebra $\mathcal{L}$ will be called the Lebesgue $\sigma$-algebra.
Outer Measures
First of all, we define an outer measure, a tool that constructs $\sigma$-algebra and measurements on the collection of sets. To motivate the high-level idea, recall that the area under the curve on the plane, i.e. Riemann integral. We approximated it by the sum of the areas of infinite number of rectangles that cover the area from above and below, divided by a grid. And the limits of these approximations provides the inner and outer area, and if they are equal, their common value is the area. In that sense, we generalize this intuition with outer measure in measure theory. Let $X$ be a set.
An outer measure is a function $\mu^*$ defined on the collection of all subsets of $X$ satisfying
- $\mu^* (\emptyset) = 0$;
- monotonicity
if $A \subset B$, then $\mu^* (A) \leq \mu^* (B)$; -
sub-additivity
$\mu^* \left( \bigcup_{i=1}^\infty A_i \right) \leq \sum_{i=1}^\infty \mu^* (A_i)$ whenever $A_1, A_2, \dots$ are subsets of $X$.
Notice that it is defined in different ways from the measure, so that some properties of measures might not be inherited; for example, there are no general rules about continuity from below and above of outer measure.
For counterexample, let $X = \mathbb{N}$ and define
\[\begin{aligned} \mu^* (A) = \begin{cases} 0 & \quad A = \emptyset \\ 1 & \quad A \text{ is finite } \\ 2 & \quad A \text{ is infinite } \\ \end{cases} \end{aligned}\]Then \(A_n = \{ 1, 2, \cdots, n \} \uparrow \mathbb{N}\) but \(\mu^* (A_n) = 1\) and \(\mu^* (A) = 2\). For \(B_n = \{ n, n+1, n+2, \cdots \} \downarrow \emptyset\), \(\mu^*(B_n) = 2\) but \(\mu^* (B) = 0\).
Also, for a finite measure space $(X, \mathcal{A}, \mu)$, define
\[\begin{aligned} \mu^* (A) = \text{inf } \left\{ \mu(B) \middle| A \subset B, B \in \mathcal{A} \right\} \end{aligned}\]One can easily show that it is outer measure. And we can show that if $A_n \uparrow A$ for subsets $A_n, A \subset X$, then $\mu^* (A_n) \uparrow \mu^*(A)$.
$\color{black}{\mathbf{Proof.}}$
It is obvious that $\lim_{n \to \infty} \mu^* (A_n) \leq \mu^* (A)$.
For each $n$, choose $B_n \in \mathcal{A}$ such that $A_n \subset B_n$ and
\[\begin{aligned} \mu^* (B_n) < \mu^* (A_n) + \frac{1}{n} \end{aligned}\]We want to find sets $C_n$ such that
- For large $N$, $\mu (C_n) \leq \mu (B_n)$ for all $n \geq N$
- If $x \in B_n$ for all $n \geq N$, then $x \in C_n$ for all $n \geq N$ too.
To do so, intuitively we employ the form of limit inferior: define $C_n = \bigcap_{k = n}^\infty B_k$. Then, $C_n$ increasing, i.e. $C_n \uparrow C$. As $\mathcal{A}$ is $\sigma$-algebra, note that $C_n, C \in \mathcal{A}$ for each $n \in \mathbb{N}$. In other words, $\mu^* (C_n) = \mu(C_n) \uparrow \mu^* (C) = \mu(C)$.
Then,
\[\begin{aligned} x \in A \rightarrow x \in A_n \; \forall n \geq N \text{ for some large } N \Rightarrow x \in B_n \; \forall n \geq N \Rightarrow x \in C_n \; \forall n \geq N \end{aligned}\]Thus $A \subset C$. We conclude that
\[\begin{aligned} \lim_{n \to \infty} \mu^* (A_n) & \geq \underset{n}{\text{lim inf}} (\mu^* (B_n) - \frac{1}{n}) \\ & \geq \lim_{n \to \infty} (\mu^* (C_n) - \frac{1}{n}) = \mu^* (C) \geq \mu^* (A) \\ \end{aligned}\] \[\tag*{$\blacksquare$}\]Inspired by the approximation of Riemann integral on $\mathbb{R}^n$, a common way to generate outer measures is as follows:
Define $$ \begin{aligned} \mu^* (E) = \text{inf } \left\{ \sum_{i=1}^\infty \ell (A_i) \; \middle| \; A_i \in \mathcal{C} \text{ for each } i \text{ and } E \subset \bigcup_{i=1}^\infty A_i \right\} \end{aligned} $$
$\color{#bf1100}{\mathbf{Proof.}}$
The first and second definition of outer measure are obivous. In case of monotonicity, assume $A \subset B$. Let $A_i \in \mathcal{C}$ for each $i$ and $B \subset \bigcup_{i=1}^\infty A_i$. Then, $A \subset \bigcup_{i=1}^\infty A_i$. From the property of the infimum, $\mu^* (A) \leq \sum_{i=1}^\infty \ell (A_i)$. By taking the infimum of the RHS, we have $\mu^* (A) \leq \mu^* (B)$.
To prove the third one, let $A_1, A_2, \dots$ be subset of $X$ and let $\varepsilon > 0$. For each $i$, $\exists \; C_{i1}, C_{i2}, \dots \in \mathcal{C}$ such that $A_i \subset \bigcup_{j=1}^\infty C_{ij}$ and by property of infimum $\sum_{j=1}^\infty \ell (C_{ij}) \leq \mu^* (A_i) + \frac{\varepsilon}{2^i}$.
Then $\bigcup_{i=1}^\infty A_i \subset \bigcup_{i = 1}^\infty \bigcup_{j = 1}^\infty C_{ij}$ and
\[\begin{aligned} \mu^* (\bigcup_{i=1}^\infty A_i) & \leq \sum_{i=1}^\infty \sum_{j=1}^\infty \ell (C_{ij}) \\ & \leq \sum_{i=1}^\infty \mu^* (A_i) + \sum_{i=1}^\infty \frac{\varepsilon}{2^i} \\ & = \sum_{i=1}^\infty \mu^* (A_i) + \varepsilon. \end{aligned}\]Since we set arbitrary $\varepsilon$, $\mu^* (\bigcup_{i=1}^\infty A_i) \leq \sum_{i=1}^\infty \mu^* (A_i)$.
\[\tag*{$\blacksquare$}\]We want to define a measure by restricting $\mu^*$ to a strictly smaller $\sigma$-algebra than the collection of all subsets of $\mathbb{R}$. (We already see that there exists non-measurable set in this kind of measure.) To do so, we will define another measurability, which concides with the viewpoint of Riemann integral: integral exists if and only if upper integral and lower integral agree. ($\leftrightarrow$ outer measure and inner measure agree.)
Let $\mu^*$ be an outer measure. A set $A \subset X$ is $\mu^*$-measurable if $$ \begin{aligned} \mu^* (E) = \mu^* (E \cap A) + \mu^* (E \cap A^c) \end{aligned} $$ for all $E \subset X$.
Note that if you want to prove that a set $A$ is \(\mu^*\)-measurable, you only need to check $\geq$ direction since $\leq$ is natural from the axiom of outer measure \(\mu^*\).
Carathéodory theorem
And we can construct the collection of \(\mu^*\)-measurable sets, which is $\sigma$-algebra, and if we restrict \(\mu^*\) to this collection, that restriction is a measure on that collection. This statement is called Carathéodory theorem.
If $\mu^*$ is an outer measure on $X$, then the collection $\mathcal{A}$ of $\mu^*$-measurable sets is a $\sigma$-algebra. If $\mu$ is the restriction of $\mu^*$ to $\mathcal{A}$, then $\mu$ is a measure. Furthermore, $\mathcal{A}$ contains all the null sets.
$\mathbf{Proof.}$
Step 1
First we show that $\mathcal{A}$ is an algebra.
(1) $\emptyset, X \in \mathcal{A}$.
For all $E \subset X$,
\[\begin{aligned} \mu^* (E \cap \emptyset) + \mu^* (E \cap \emptyset^c) & = \mu^* (\emptyset) + \mu^* (E) \\ & = \mu^* (E) \end{aligned}\]which show both $\emptyset$ and $X$ are $\mu^*$-measurable.
(2) $A \in \mathcal{A}$ implies $A^c \in \mathcal{A}$
It is obvious.
(3) If $A, B \in \mathcal{A}$, $A \cup B \in \mathcal{A}$
From $A, B \in \mathcal{A}$, it is obvious that for all $E \subset X$ and $F \subset X$:
\[\begin{aligned} \mu^* (E) & \geq \mu^* (E \cap A) + \mu^* (E \cap A^c) \\ \mu^* (F) & \geq \mu^* (F \cap B) + \mu^* (F \cap B^c) \\ \end{aligned}\]For all $E \subset X$, from the following relation of sets:
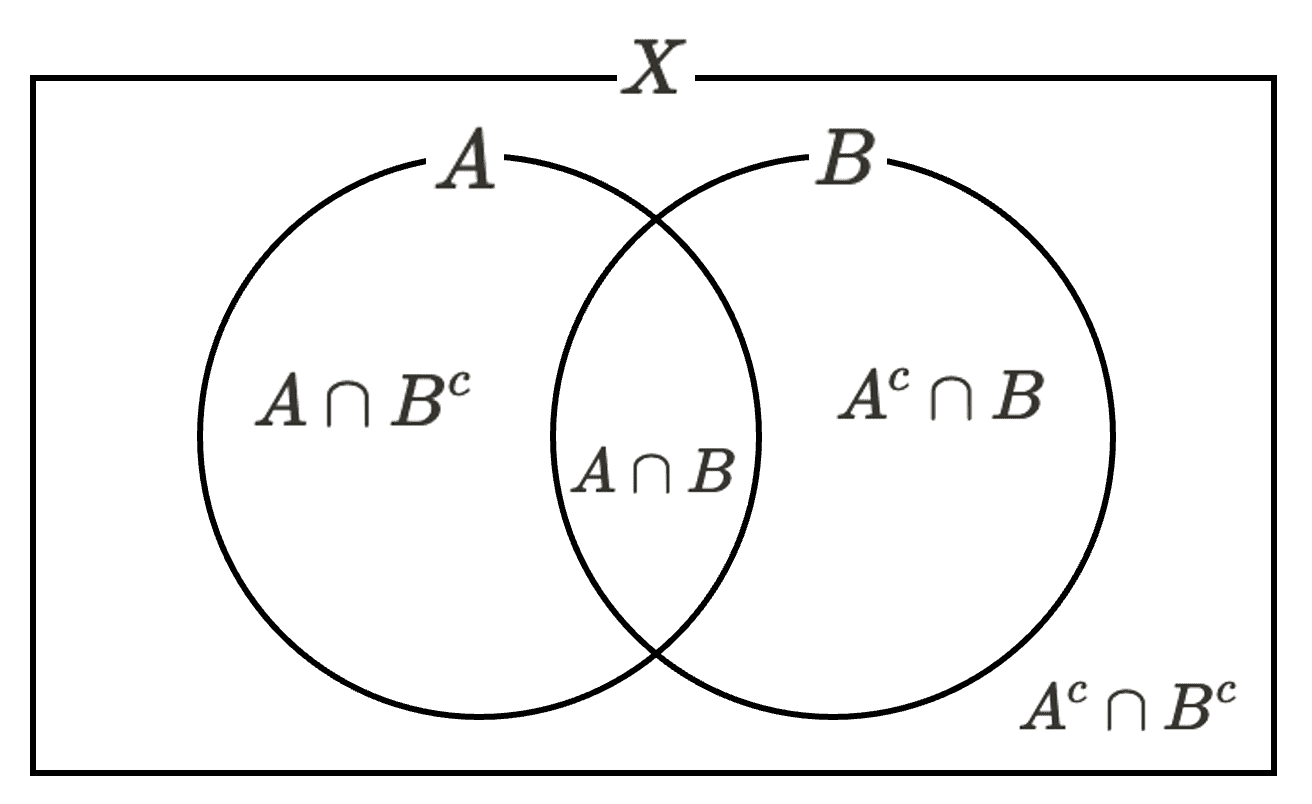
we have
\[\begin{aligned} & \mu^* \left(E \cap (A \cup B) \right) + \mu^* \left(E \cap (A \cup B) \right) \\ & = \mu^* \left(E \cap \left[ (A \cap B^c) \cup (A \cap B) \cup (A^c \cap B) \right] \right) + \mu^* \left(E \cap A^c \cap B^c \right) \\ & \leq \mu^* (\color{red}{E \cap A} \cap B^c) + \mu^* (\color{red}{E \cap A} \cap B) + \mu^* (\color{blue}{E \cap A^c} \cap B) + \mu^* (\color{blue}{E \cap A^c} \cap B^c) \\ & \leq \mu^* (\color{red}{E \cap A}) + \mu^* (\color{blue}{E \cap A^c}) \\ & \leq \mu^* (E) \end{aligned}\]Step 2
Next, now we show that $\mathcal{A}$ is a $\sigma$-algebra. And we will show this by proving that $\mathcal{A}$ is a monotone class, so that it is a $\sigma$-algebra.
Let $B_i \uparrow B$ and each $B_i \in \mathcal{A}$.
Set $A_1 = B_1$, $A_2 = B_2 - B_1$, $A_3 = B_3 - B_2$, $\dots$.
Then it is obvious that $A_i$ are pairwise disjoint.
For $\forall \; E \subset X$,
And from this equality, we also get a recurrence relation $\mu^* (E \cap B_n) = \mu^* (E \cap B_{n-1}) + \mu^* (E \cap A_n)$. Then we derive
\[\begin{aligned} \mu^* (E \cap B_n) \geq \sum_{i=1}^n \mu^* (E \cap A_i) \end{aligned}\]Hence,
\[\begin{aligned} \mu^* (E) & = \mu^* (E \cap B_n) + \mu^* (E \cap B_n^c) \\ & \geq \sum_{i=1}^n \mu^* (E \cap A_i) + \mu^* (E \cap B^c) \\ \mu^* (E) & \geq \sum_{i=1}^\infty \mu^* (E \cap A_i) + \mu^* (E \cap B^c) \text{ by letting } n \to \infty \end{aligned}\]Furthermore,
\[\begin{aligned} \mu^* (E \cap B) + \mu^* (E \cap B^c) & = \mu^* ( \bigcup_{i=1}^\infty (E \cap B_i) ) + \mu^* (E \cap B^c) \\ & = \mu^* ( \bigcup_{i=1}^\infty (E \cap A_i) ) + \mu^* (E \cap B^c) \\ & \leq \sum_{i=1}^\infty \mu^* (E \cap A_i) + \mu^* (E \cap B^c) \end{aligned}\]Thus, we have
\[\begin{aligned} \mu^* (E) \geq \mu^* (E \cap B) + \mu^* (E \cap B^c) \end{aligned}\]Thus $\mu^* (E) = \mu^* (E \cap B) + \mu^* (E \cap B^c)$. And, it also holds $\mu^* (E) = \sum_{i=1}^\infty \mu^* (E \cap A_i) + \mu^* (E \cap B^c)$. In addition, if $B_i \downarrow B$, and $B_i \in \mathcal{A}$ for each $i$. Then since $B_i^c \uparrow B^c$, from the discussion above $B^c \in \mathcal{A}$. As $\mathcal{A}$ is an algebra, $B \in \mathcal{A}$ too.
Hence $B \in \mathcal{A}$ and $\mathcal{A}$ is an algebra satisfying the monotone class condition, it is a $\sigma$-algebra also by monotone class theorem.
Step 3
Next, we show that $\mu = \mu^* \vert_{\mathcal{A}}$, i.e. $\mu$ is the restriction of $\mu^*$ to $\mathcal{A}$, is a measure.
- $\mu^* (\emptyset) = 0$ clearly.
- Let $A_i \in \mathcal{A}$ are pairwise disjoint. By taking $B = \bigcup_{i=1}^\infty A_i$, we obtain $$ \begin{aligned} \mu^* (E) = \sum_{i=1}^\infty \mu^* (E \cap A_i) + \mu^* (E \cap B^c) \; \forall \; E \subset X \end{aligned} $$ Since $\mathcal{A}$ is a $\sigma$-algebra, by taking $E = B$, we have $$ \begin{aligned} \mu^* (B) = \sum_{i=1}^\infty \mu^* (A_i) \end{aligned} $$
Step 4
Finally, we claim that $\mathcal{A}$ contains all the null sets.
Assume $\mu^* (A) = 0$. Then, for each $E \subset X$, we have
\[\begin{aligned} \mu^* (E \cap A) + \mu^* (E \cap A^c) & \leq \mu^* (A) + \mu^* (E \cap A^c) \\ & = \mu^* (E \cap A^c) \\ & \leq \mu^* (E) \end{aligned}\]Hence $\mu^* (E) = \mu^* (E \cap A) + \mu^* (E \cap A^c)$, i.e. $A \in \mathcal{A}$.
\[\tag*{$\blacksquare$}\]Lebesgue-Stieltjes measures
Let $X = \mathbb{R}$, $\mathcal{C}$ be the collection of intervals of the form $(a, b]$, i.e. \(\mathcal{C} = \{ (a, b] \mid a, b \in \mathbb{R}, a < b\}\). Let $\alpha(x)$ be an increasing right continuous function, that is
\[\begin{aligned} \alpha (x) \leq \alpha(y) \text{ if } x < y \\ \lim_{z \to x+} \alpha (z) = \alpha(x) \; \forall x \end{aligned}\]Define $\ell ( (a, b] ) = \alpha(b) - \alpha(a)$. Also, let’s construct an outer measure $m^*$ as $\mathbf{Proposition\ 1.}$:
\[\begin{aligned} m^*(E)=\inf \left\{\sum_{i=1}^{\infty} \ell\left(A_i\right): A_i \in \mathcal{C} \text { for each } i \text { and } E \subset \cup_{i=1}^{\infty} A_i\right\} \end{aligned}\]Then, we claim that the measure of a half-open interval $(e, f]$ is equal to the length of interval.
First, we need the following lemma:
$\color{green}{\mathbf{Proof.}}$
Since \(\{ J_k \}\) is a cover of $[C, D]$, there exists at least one interval \(J_{k_1}\) such that \(C \in J_{k_1}\).
If \(J_{k_1} = (a_{k_1}, b_{k_1})\) covers $[C, D]$, we stop. Otherwise, \(b_{k_1} \leq D\) and there must be at least one interval \(J_{k_2}\) such that \(b_{k_1} \in J_{k_2}\).
If \([C, D] \subset J_{k_1} \cup J_{k_2}\), we stop. Otherwise, \(b_{k_1} < b_{k_2} \leq D\) and there must be at least one interval \(J_{k_3}\) such that \(b_{k_2} \in J_{k_3}\).
We continue until we have covered $[C, D]$ with intervals \(J_{k_1}, \dots, J_{k_m}\) that at each stage we choose \(b_{k_{i-1}} \in J_{k_i}\). We can ensure that the procedure will stop for some $m \leq n$, since \(\{J_k \}\) is a finite cover of $[C, D]$.
Then, by our construction we have
\[\begin{aligned} a_{k_1} < &C < b_{k_1} \\ a_{k_j} < &b_{k_{j - 1}} < b_{k_j} \text{ for } 2 \leq j \leq m \\ a_{k_m} < &D < b_{k_m} \\ \end{aligned}\]Then
\[\begin{aligned} \alpha(D)-\alpha(C) \leq & \alpha\left(b_{k_m}\right)-\alpha\left(a_{k_1}\right) \\ = & \left[\alpha\left(b_{k_m}\right)-\alpha\left(b_{k_{m-1}}\right)\right]+\left[\alpha\left(b_{k_{m-1}}\right)-\alpha\left(b_{k_{m-2}}\right)\right]+\cdots \\ & \quad+\left[\alpha\left(b_{k_2}\right)-\alpha\left(b_{k_1}\right)\right]+\left[\alpha\left(b_{k_1}\right)-\alpha\left(a_{k_1}\right)\right] \\ \leq & \left[\alpha\left(b_{k_m}\right)-\alpha\left(a_{k_m}\right)\right]+\left[\alpha\left(b_{k_{m-1}}\right)-\alpha\left(a_{k_{m-1}}\right)\right]+\cdots \\ & \quad+\left[\alpha\left(b_{k_2}\right)-\alpha\left(a_{k_2}\right)\right]+\left[\alpha\left(b_{k_1}\right)-\alpha\left(a_{k_1}\right)\right] . \end{aligned}\]Since \(\{ J_{k_1}, \cdots J_{k_m} \} \subseteq \{ J_{1}, \cdots J_{n} \}\), done.
\[\tag*{$\blacksquare$}\]Then, we can show that following: $m^*(I)$ is a natural extension of length of $I$
$\color{#bf1100}{\mathbf{Proof.}}$
(1) $m^* (I) \leq \ell(I)$.
Let $A_1 = I$ and $A_2 = A_3 = \cdots = \emptyset$. Then $I \subset \bigcup_{i=1}^\infty A_i$. By definition of infimum,
\[\begin{aligned} m^* (I) \leq \sum_{i=1}^\infty \ell (A_i) = \ell(A_1) = \ell (I) \end{aligned}\](2) $m^* (I) \geq \ell(I)$.
Let $I \subset \bigcup_{i=1}^\infty A_i$ where $A_i = (c_i, d_i]$. Let $\varepsilon > 0$ and choose $c \in (e, f)$ such that $\alpha(c) - \alpha(e) < \frac{\varepsilon}{2}$.
Note that this is possible due to the right continuity of $\alpha$. Similarly, we can choose $d^{\prime}_i > d_i$ such that $\alpha(d^{\prime}_i) - \alpha(d_i) < \frac{\varepsilon}{2^{i+1}}$ for each $i$.
Then $[c, f] \subset \bigcup_{i=1}^\infty (c_i, d_i] \subset \bigcup_{i=1}^\infty (c_i, d_i^\prime)$. As $[c, f]$ is compact, we can choose a finite subcover, i.e. $j_1, \cdots, j_n$ for some $n \in \mathbb{N}$ such that $[c, f] \subset \bigcup_{i=1}^n (c_{j_i}, d_{j_i}^\prime)$.
Then it follows from the previous lemma:
\[\begin{aligned} \ell (I) & \leq \alpha (f) - \alpha (c) + \varepsilon/2 \leq \sum_{k=1}^n (\alpha (d_{j_k}^\prime) - \alpha (c_{j_k})) + \varepsilon/2 \\ & \leq \sum_{i=1}^\infty \left[(\alpha (d_{i}) + \varepsilon / 2^{i+1}) - \alpha (c_{i}) \right] + \varepsilon / 2 \\ & = \sum_{i=1}^\infty \ell(A_i) + \varepsilon \end{aligned}\]Then, by taking an infimum to the RHS, we obtain $\ell (I) \leq m^* (I) + \varepsilon$. Since $\varepsilon > 0$ is arbitrary, we conclude that $m^* (I) \geq \ell (I)$.
\[\tag*{$\blacksquare$}\]The next step in the construction of Lebesgue-Stieltjes measure corresponding to $\alpha$ is to show that every set constructed by intervals is measurable with respect to our measure $m^*$. Formally, we show the following statement:
Since every open set can be written as the countable union of disjoint open intervals, therefore every open set and closed set on $\mathbb{R}$ is $m^*$-measurable.
$\color{#bf1100}{\mathbf{Proof.}}$
Recall that the collection of \(m^*\)-measurable sets is $\sigma$-algebra. Since Borel $\sigma$-algebra is generated by \(\{ (a, b] \mid a, b \in \mathbb{R} \}\), it suffices to show that every interval $J$ of the form $(c, d]$ is \(m^*\)-measurable.
Let $E$ be any set with $m^* (E) < \infty$. (Note that $m^* (E) = \infty$ is trivial.) Then we need to show
\[\begin{aligned} m^* (E) \geq m^* (E \cap J) + m^* (E \cap J^c). \end{aligned}\]Choose $I_1, I_2, \dots,$ where $I_i = (a_i, b_i]$, such that $E \subset \bigcup_i I_i$ and by property of infimum
\[\begin{aligned} m^* (E) \geq \sum_i \left[ \alpha(b_i) - \alpha(a_i) \right] - \varepsilon = \sum_i m^* (I_i) - \varepsilon. \end{aligned}\]Since $E \subset \bigcup_i I_i$,
\[\begin{aligned} m^* (E \cap J) & \leq \sum_i m^* (I_i \cap J) \\ m^* (E \cap J^c) & \leq \sum_i m^* (I_i \cap J^c) \end{aligned}\]By summing them,
\[\begin{aligned} m^* (E \cap J) + m^* (E \cap J^c) \leq \sum_i \left[ m^* (I_i \cap J) + m^* (I_i \cap J^c) \right]. \end{aligned}\]We claim that $m^* (I_i \cap J) + m^* (I_i \cap J^c) = m^* (I_i)$. So, what we want to show is $m^* (I_i \cap J) + m^* (I_i \cap J^c) \leq m^* (I_i)$.
Note that $I_i \cap J$ is an interval (possibly empty) that is open on the left and closed on the right. If we set $K_1 = (-\infty, c]$ and $K_2 = (d, \infty)$, both $I_i \cap K_1$ and $I_i \cap K_2$ are also open on the left and closed on the right (and possibly either $I_i \cap K_1$ or $I_i \cap K_2$ or both might be empty, depending on the relative locations of $I_i$ and $J$).
Note that $J^c = K_1 \cup K_2$. And if $K = (a, b]$ and $L = (b, c]$, then $K \cup L = (a, c]$ and $\ell(K) + \ell(L) = \alpha (c) - \alpha (a) = \ell(K \cup L)$. From this fact,
\[\begin{aligned} m^* (I_i \cap J) + m^* (I_i \cap J^c) & \leq m^* (I_i \cap K_1) + m^* (I_i \cap J) + m^* (I_i \cap K_2) \\ & = \ell (I_i \cap K_1) + \ell (I_i \cap J) + \ell (I_i \cap K_2) \\ & = \ell (I_i) = m^* (I_i). \end{aligned}\]Thus
\[\begin{aligned} m^* (E \cap J) + m^* (E \cap J^c) \leq \sum_i m^* (I_i) \leq m^* (E) + \varepsilon. \end{aligned}\]Since $\varepsilon$ is arbitrary, done.
\[\tag*{$\blacksquare$}\]Hence we will drop the asterisks from \(m^*\) and call this special form of measure as Lebesgue-Stieltjes measure. In the special case where $\alpha(x) = x$, $m$ is referred to as Lebesgue measure. In addition, in the special case of Lebesgue measure, the collection of \(m^*\)-measurable sets is called the Lebesgue $\sigma$-algebra. And a set is Lebesgue measurable if it is in the Lebesgue $\sigma$-algebra. For example, as we saw in $\mathbf{Proposition\ 3}$, every Borel set on $\mathbb{R}$ is Lebesgue measurable. But one should aware that not all Lebesgue measurable set is Borel measurable; we will see an example with Cantor function in the next post.
Here are some examples.
click to expand
$\color{green}{\mathbf{Example\ 1.}}$ Let $m$ be Lebesgue measure. If $x \in \mathbb{R}$, then \(\{ x \}\) is closed set thus Borel measurable. And
\[\begin{aligned} m( \{ x \}) = \lim_{n \to \infty} m ( (x - \frac{1}{n}, x]) = \lim_{n \to \infty} x - x + \frac{1}{n} = 0 \end{aligned}\]Thus,
\[\begin{aligned} m( (a, b) ) & = m ( (a, b] ) - m ( \{ b \} ) = b - a \\ m ( [a, b] ) & = m ( (a, b] ) + m ( \{ b \} ) = b - a \\ \end{aligned}\]Thus what does it implies is, adding 0 to itself countably many times is still 0, so the Lebesgue measure of a countable set is 0. Since $\sigma$-algebras are closed under the operation of countable unions, note that countable sets are Borel measurable.
$\color{green}{\mathbf{Example\ 2.}}$ Cantor set
Construct
by continuing removing middle thirds. Then, we call $C = \bigcap_n C_n$ Cantor set.

$\mathbf{Fig\ 1.}$ Cantor set
Recall that
-
Cantor set is closed
$\mathbf{Proof.}$
It is because Cantor set is intersection of closed set (complement of $(a, b)$). Note that intersections of closed subsets are also closed. This can be derived using De Morgan's Law and the axiom of a topology that unions of open subsets are also open. $$\tag*{$\blacksquare$}$$ -
Cantor set is uncountable
$\mathbf{Proof.}$
Let any element $a \in C$ be given. Then, we can represent any element $a$ with binary number. Precisely, if $a$ is contained in the first third part of $C_1$, then choose $a_1 = 0$. Otherwise, choose $a_1 = 1$. Without loss of generality, suppose $a_1 = 0$. Then, if $a$ is contained in the first third part of the first third part of $C_1$, choose $a_2 = 0$. Otherwise, if it is contained in the second third part of the first third part of $C_1$, choose $a_2 = 1$. Continuing this procedure, we obtain $a_1, a_2, \cdots \in \{0, 1\}$. Hence, $$ \begin{aligned} 2^{| \mathbb{N} |} \leq | F | \end{aligned} $$ which implies $C$ is uncountable. $$\tag*{$\blacksquare$}$$ -
Cantor set doesn't contain any interval that is subset of $[0, 1]$.
$\mathbf{Proof.}$
Note that the length of $C_n$ is $$ \begin{aligned} \sum_{i=1}^n \frac{2^{n-1}}{3^n} = \frac{2}{3}^n \end{aligned} $$ Thus, the length of $C$ is $$ \begin{aligned} \lim_{n \to \infty} \frac{2}{3}^n = 0. \end{aligned} $$ In other words, Lebesgue measure of Cantor set $C$ is zero. $$\tag*{$\blacksquare$}$$ -
and every point is a limit point
$\mathbf{Proof.}$
Let $x \in C$, and let $S$ be an open interval containing $x$. Let $I_n$ be the closed interval in $C_n$ (of which there are $2^n$) that contains $x$. Choose $n$ large enough so that $I_n \subset S$. Note that it always exist such $n$ since Cantor set doesn't contain any open interval. Let $x_n$ be an endpoint of $I_n$ such that $x_n \neq x$. Now, by construction, $x_n \in C$. Hence, $$(S - \{x \}) \cap C \neq \emptyset$$, i.e. $x$ is a limit point: an arbitrary open interval $S$ containing $x$ contains at least one element of $C$. $$\tag*{$\blacksquare$}$$
Then define a function $f_0: [0, 1] \to [0, 1]$ to be $\frac{1}{2}$ on the interval $( \frac{1}{3}, \frac{2}{3})$, to be $\frac{1}{4}$ on $(\frac{1}{9}, \frac{2}{9})$, to be $\frac{3}{4}$ on $(\frac{7}{9}, \frac{8}{9})$, and so on.
\[\begin{aligned} f (x) = \begin{cases} \text{inf } \left\{ f_0 (y) \mid y \geq x, y \neq C \right\} & \text{ if } x < 1\\ 1 & \text{ if } x = 1\\ \end{cases} \end{aligned}\]And this definition implies that $f = f_0$ on the complement of the Cantor set.
Since $f$ is increasing, so it has only jump discontinuities. But if it has a jump discontinuity, there will be a rational of the form $k / 2^n$ with $k \leq 2^n$ that is not in the range of $f$. But by the construction, each of the values \(\{ k/2^n \mid n \geq 0, k \leq 2^n \}\) is taken by $f_0$ for some point in the complement of $C$, and so is taken by $f$. The only way this can happen is if $f$ is continuous. This function $f$ is called Cantor-Lebesgue function or sometimes simply the Cantor function

$\mathbf{Fig\ 2.}$ Cantor function $f$
file:///Users/leeyngdo/Downloads/cantor_set_function.pdf
$\color{green}{\mathbf{Example\ 3.}}$ Generalized Cantor set
For now, let us follow the construction of the Cantor set, with this difference. Instead of removing the middle third at the first stage, remove that middle fourth $(\frac{3}{8}, \frac{5}{8})$. On each of the two intervals that remain, remove the middle sixtennths. On each of the four intervals that remain, remove the middle interval of length $\frac{1}{64}$, and so on. Then the total length of intervals that we remove is
But, again the remaining set contains no intervals, is closed and uncountable, every point is a limit point, and has measure $1/2$. Of course, other choices than $\frac{1}{4}$, $\frac{1}{16}$, etc. are possible.
$\color{green}{\mathbf{Example\ 4.}}$ Let $q_1, q_2, \cdots$ be an enumeration of the rational numbers, let $\varepsilon > 0$, and let $I_i = (q_i - \varepsilon/2^i, q_i + \varepsilon/2^i)$. Then the measure of $I_i$ is $\varepsilon/2^{i-1}$, hence the measure of $\cup_i I_i$ is at most $2 \varepsilon$. Therefore the measure of $A = [0, 1] - \cup_i I_i$ is larger than $1 - 2 \varepsilon$, but $A$ contains no rational numbers.
\(\tag*{$\blacksquare$}\)
In summary, via above examples we observe that
- countable set has Lebesgue measure of 0
- uncountable set can have Lebesgue measure of 0
- e.g. Cantor set
- a set of measure greater than 0 may not contain any interval
- e.g. generalized Cantor set
Let $A \subset \mathbb{R}$ be a Lebesgue measurable set. We will show that $A$ is “almost equal” to the countable intersection of open sets and “almost equal” to the countable union of closed sets.
Here, the countable intersections of open sets are often called $G_\delta$ sets: $G$ for geoffnet (German word of open) and $\delta$ for Durchschnitt (German word for intersection). And the countable unions of closed sets are often called $F_\sigma$ sets: $F$ for fermé (German word of closed) and $\sigma$ for Summe (German word for union).
Suppose $A \subset \mathbb{R}$ is a Lebesgue measurable set. Let $m$ be Lebesgue measure.
- Outer approximation by open sets
Given $\varepsilon > 0$, there exists an open set $G$ that contains $A$ such that $m ( G - A ) < \varepsilon$. - Inner approximation by closed sets
Given $\varepsilon > 0$, there exists a closed set $F$ contained in $A$ such that $m ( A - F ) < \varepsilon$. - Outer approximation by $G_\delta$
There exists a set $H$ which contains $A$ that is the countable intersection of a decreasing sequence of open sets and $m(H - A) = 0$. - Inner approximation by $F_\sigma$
There exists a set $F$ which is contained $A$ that is the countable union of a increasing sequence of closed sets and $m(A - F) = 0$.
$\color{#bf1100}{\mathbf{Proof.}}$
(1) There exists a set $E$ of the form $\bigcup_{j=1}^\infty (a_j, b_j]$ such that $A \subset E$ and $m(E) < m(A) + \frac{\varepsilon}{2}$, i.e. $m(E - A) < \frac{\varepsilon}{2}$. Let $G = \bigcup_{j=1}^\infty (a_j, b_j + \frac{\varepsilon}{2^{j+1}})$. Then $G$ is open containing $A$ and
\[\begin{aligned} m(G - E) = m(G) - m(E) < \varepsilon \sum_{j=1}^\infty \frac{1}{2^{j + 1}} = \frac{\varepsilon}{2}. \end{aligned}\]Therefore
\[\begin{aligned} m(G - A) \leq m(G - E) + m(E - A) < \varepsilon \end{aligned}\](2) Suppose $A$ is bounded. Since any closed sets are Lebesgue measurable, $\bar{A} - A$ is also Lebesgue measurable. Then, by (1), we can choose an open $G \supset \bar{A} - A$ such that $m(G) < m(\bar{A} - A) + \varepsilon$.
Set $F = \bar{A} - G$. Then, $F$ is a closed set as it is an intersection of closed set, compact, and also contained in $A$. And
\[\begin{aligned} m(F) & = m(A) - m(A \cap G) = m(A) - [m(G) - m(G - A)] \\ & \geq m(A) - m(G) + m (G - A) \geq m (A) - m(G) + m(\bar{A} - A) > m(A) - \varepsilon. \end{aligned}\]Now, suppose $E$ is unbounded, and let $E_j = E \cap (j, j+1]$. By preceding idea, there exists $K_j \subset E_j$ with $m(E_j - K_j) < \frac{\varepsilon}{2^{j}}$. Let $F_n = \bigcup_{j = -n}^n K_j$. Then, $F_n \subset E$, and $m (F_n) \geq m (\bigcup_{j=-n}^n E_j) - \varepsilon$. Since $m (E) = \lim_{n \to \infty} m (\bigcup_{j=-n}^n E_j)$, the result follows.
(3) First, suppose $\mu (A) < \infty$. Then, for each $j \in \mathbb{N}$ we can choose an open $G_j \supset A$ such that
\[\begin{aligned} \mu (G_j) - \frac{1}{2^j} \leq \mu (A) \end{aligned}\]Let $G_\delta = \bigcap_{j=1}^\infty G_j$. Then $E \subset G_\delta$ and $\mu (G_\delta) = \mu (A) < \infty$, so that $\mu (G_\delta - A) = 0$.
Now, assume that $\mu (A) = \infty$. Set $A_n = A \cap (n, n+1]$ for $n \in \mathbb{Z}$. Then each Lebesgue measurable $A_n$ with $\mu (A_n) < \infty$, there exists $G_\delta$ set $G_n$. Then, $G = \bigcup_{n \in \mathbb{Z} G_n}$ is a set that we desired.
(4) By (3), for $A^c$ we have $G_\delta \supset A^c$ such that $m (G_\delta - A^c) = 0$. Then, done by setting $F_\sigma = G_\delta^c$.
\[\tag*{$\blacksquare$}\]
Such properties that every measurable set can be approximated from above by open measurable sets and from below by compact measurable sets are called regularity. For much detail, see this.
Although we restrict $\mathbf{Proposition\ 4}$ to Lebesgue measure, the analogue of it holds for any Lebesgue-Stieltjes measure $\mu$:
$\color{blue}{\mathbf{Proof.}}$
Let $A$ and $E$ be chosen as in the proof of part (1) of $\color{#bf1100}{\mathbf{Proposition\ 4}}$ with $m$ replaced by $\mu$. Since $\mu ((a_j, b_j ]) = \lim_{y \to b_j +} \mu ((a_j, y))$, we can choose $c_j > b_j$ such that
\[\begin{aligned} \mu ((a_j, c_j)) \leq \mu((a_j, b_j]) + \varepsilon 2^{- (j + 1)} \end{aligned}\]Let $G = \bigcup_{j=1}^\infty (a_j, c_j)$. Then $E \subset G$ and
\[\begin{aligned} \mu (G - E) \leq \sum_{j=1}^\infty \mu ((a_j, c_j)) - \mu ((a_j, b_j]) \leq \sum_{j=1}^\infty \frac{\varepsilon}{2^{j+1}} = \frac{\varepsilon}{2}. \end{aligned}\]We now proceed exactly as in the proof of $\color{#bf1100}{\mathbf{Proposition\ 4}}$.
\[\tag*{$\blacksquare$}\]Carathéodory Extension Theorem
Let $\mathcal{A}_0$ be an algebra of a set $X$. A pre-measure is a function $\mu_0: \mathcal{A}_0 \to [0, \infty)$ such that
- $\mu_0 (\emptyset) = 0$;
- countable additivity ($\sigma$-additivity): if $A_i \in \mathcal{A}$, $i = 1, 2, \dots$, are pairwise disjoint, i.e. $A_i \cap A_j = \emptyset$ if $i \neq j$, then $$ \begin{aligned} \mu_0 \left( \bigcup_{i=1}^\infty A_i \right) = \sum_{i=1}^\infty \mu_0 (A_i). \end{aligned} $$
In many cases it is not easy to define a measure on all sets $E$ in a $\sigma$-algebra. Carathéodory extension theorem abstracts some of the techniques used above to give a tool for constructing measures in a variety of contexts and shows that it is sufficient to define a measure on an algebra $\mathcal{A}_0$.
Suppose $\mathcal{A}_0$ is an algebra on a set $X$ and $\ell : \mathcal{A}_0 \to [0, \infty]$ is a pre-measure on $\mathcal{A}_0$. Define $$ \begin{aligned} \mu^* (E) = \text{inf } \left\{ \sum_{i=1}^\infty \ell (A_i) \; \middle| \; \text{ each } A_i \in \mathcal{A}_0, \; E \subset \bigcup_{i=1}^\infty A_i \right\} \end{aligned} $$ for $E \subset X$. Then
- $\mu^*$ is an outer measure;
- $\mu^* (A) = \ell (A)$ if $A \in \mathcal{A}_0$;
- every set in $\mathcal{A}_0$ and every $\mu^*$-null set is $\mu^*$-measurable;
- if $\ell$ is $\sigma$-finite, then there is a unique extension to $\sigma ( \mathcal{A}_0 )$.
$\color{red}{\mathbf{Proof.}}$
(1) We already proved in $\color{#bf1100}{\mathbf{Proposition\ 1}}$.
(2) It is clear that $\mu^* (A) \leq \ell (A)$; set $A_1 = A$ and $A_2 = A_3 = \cdots = \emptyset$. In case of $\ell (A) \leq \mu^* (A)$, it suffices to show that $\ell (A)$ is a lower bound of any $\sum_{i = 1}^\infty \ell (A_i)$ such that each \(A_i \in \mathcal{A}_0\) and $A \subset \bigcup_{i=1}^\infty A_i$.
Suppose \(A \subset \bigcup_{i=1}^\infty A_i\) with \(A_i \in \mathcal{A}_0\). Let $B_1 = A \cap A_1$, $B_2 = A \cap (A_2 - A_1)$, $B_3 = A \cap (A_3 - (A_1 \cup A_2))$, and so on. In other words, for $n \geq 2$, $B_n = A \cap (A_n - (\bigcup_{i=1}^{n-1} A_i))$.
Then $B_n \uparrow A$ and $B_n \in \mathcal{A}_0$ $B_n \subset A_n$ for each $n$. Therefore, by $\sigma$-additivity of pre-measure:
\[\begin{aligned} \ell (A) = \sum_{i=1}^\infty \ell (B_i) \leq \sum_{i=1}^\infty \ell (A_i). \end{aligned}\](3) Suppose \(A \in \mathcal{A}_0\). Let any $\varepsilon > 0$ be given, and let $E \subset X$. Then, by property of infimum we can find \(B_1, B_2, \dots \in \mathcal{A}_0\) such that $E \subset \bigcup_{i=1}^\infty B_i$ and \(\sum_i \ell (B_i) \leq \mu^* (E) + \varepsilon\).
Without loss of generality, we may assume that $\mu^* (E) < \infty$. If not, it is trivial. Hence, we can split the infinite sum as follows:
\[\begin{aligned} \sum_{i=1}^\infty \ell (B_i) = \sum_{i=1}^\infty \ell (B_i \cap A) + \sum_{i=1}^\infty \ell (B_i \cap A^c) \end{aligned}\]Thus,
\[\begin{aligned} \mu^* (E \cap A) + \mu^* (E \cap A^c) & \leq \sum_{i=1}^\infty \ell (B_i \cap A) + \sum_{i=1}^\infty \ell (B_i \cap A^c) \\ & = \sum_{i=1}^\infty \ell (B_i) \leq \mu^* (E) + \varepsilon \end{aligned}\]Since $\varepsilon > 0$ is arbitrary, done.
Null set case is trivial by monotonicity of outer measure; if \(\mu^* (N) = 0\) then for any $E \subset X$:
\[\begin{aligned} \mu^* (E \cap N) + \mu^* (E \cap N^c) \leq \mu^* (N) + \mu^* (E) = \mu^* (E) \end{aligned}\](4) Suppose we have two extensions to \(\sigma (\mathcal{A}_0)\): one is \(\mu^*\) and let the other extension be called $\nu$. We will show that \(\mu^* (E) = \nu (E)\) for any \(E \in \sigma (\mathcal{A}_0)\). As $\ell$ is $\sigma$-finite, we can write $X = \bigcup_{i=1}^\infty K_i$ where $K_i \uparrow X$ and $\ell (K_i) < \infty$ for each $i$. First of all, we will show that there is an unique extension to $\sigma (\mathcal{A}_0)$ if $\ell$ is finite. Then, it proves the theorem, since if we have two extensions of $\ell$, $\mu$ and $\nu$, for $A \in \sigma (\mathcal{A}_0)$
\[\begin{aligned} \mu (A) = \lim_{n \to \infty} \mu (A \cap K_n) = \lim_{n \to \infty} \nu (A \cap K_n) = \nu (A) \end{aligned}\]which shows $\mu = \nu$.
Suppose that \(\mu^*\) is a finite measure.
- $\nu (E) \leq \mu^* (E)$.
If $E \in \sigma(\mathcal{A}_0)$, then $E$ is $\mu^*$-measurable, so that there exist $A_i \in \mathcal{A}_0$ such that $E \subset \bigcup_{i=1}^\infty A_i$. Since $\nu$ and $\mu^*$ are both extensions to $\sigma (\mathcal{A}_0)$ of $\ell$, $\ell = \nu$ on $\mathcal{A}_0$, therefore $\sum_{i} \ell (A_i) = \sum_{i} \nu (A_i)$. Hence, $$ \begin{aligned} \nu (E) \leq \sum_{i=1}^\infty \nu (A_i) = \sum_{i=1}^\infty \ell (A_i) \end{aligned} $$ hence done by definition of infimum. - $\nu (E) \geq \mu^* (E)$.
By property of infimum, pick $A_i \in \mathcal{A}_0$ for each $i$ where $\mu^* (E) + \varepsilon \geq \sum_{i=1}^\infty \ell (A_i)$ and $E \subset A = \bigcup_{i=1}^\infty A_i$. From this, $\mu^* (A - E) \leq \varepsilon$.
Define $B_k = \bigcup_{i=1}^k A_i$. Then $B_k \in \mathcal{A}_0$ and $\ell (B_k) = \nu (B_k) = \mu^* (B_k)$ and $B_k \uparrow A$. Then, by continuity from below of pre-measure, $$ \begin{aligned} \mu^* (A) = \lim_{k \to \infty} \mu^* (B_k) = \lim_{k \to \infty} \nu (B_k) = \nu (A). \end{aligned} $$ Therefore $$ \begin{aligned} \mu^* (E) & \leq \mu^* (A) = \nu (A) = \nu (E) + \nu (A - E) \\ & \leq \nu (E) + \mu^* (A - E) \leq \nu (E) + \varepsilon. \end{aligned} $$
Reference
[1] Richard F. Bass, Real Analysis for Graduate Students, Version 4.3
[2] Wikipedia, Measurable space
[3] Demystifying the Caratheodory Approach to Measurability
[4] Show that every point of cantor set is a limit point
[5] Wikiepedia, Pre-measure

Leave a comment