[Measure Theory] Measurable Functions

In the classical theory of integration on $\mathbb{R}$, $\int_{a}^b f(x) \; dx$ is defined as a limit of Riemann sums. However, there exists a set whose size cannot be measured by Riemann integrals. For example, Dirichlet function, a characteristic function of $\mathbb{Q}$:

\[\begin{aligned} \mathbf{1}_{\mathbb{Q}} (x) = \begin{cases} 1 \quad & x \in \mathbb{Q} \\ 0 \quad & x \notin \mathbb{Q} \\ \end{cases} \end{aligned}\]

is one of the most well-known functions that are not Riemann Integable. Therefore, mathematicians naturally questioned whether they could define the size of sets without Riemann integrability and endeavored to formulate a novel concept, capable of resolving this issue. Consequently, Henri Lebesgue (1875-1941) introduced the Lebesgue measure and pioneered the Lebesgue integration for Lebesgue-measurable sets.

But before we delve into the Lebesgue integration thoery, we begin our discussion with moving our interest of measurable sets to measurable functions.

Measurability

Suppose we have a measurable space $(X, \mathcal{A})$.

$\color{blue}{\mathbf{Definition.}}$ Measurability of function
A function $f: X \to \mathbb{R}$ is measurable or $\mathcal{A}$ measurable if $$f^{-1} \left( (a, \infty) \right) = \{ x \mid f(x) > a \} \in \mathcal{A}$$ for all $a \in \mathbb{R}$.

A complex-valued function is measurable if both its real and imaginary parts are measurable. If $X$ is a metric space and $\mathcal{B}$ is the Borel $\sigma$-algebra. If $f: X \to \mathbb{R}$ is measurable with respect to $\mathcal{B}$, then we say $f$ is Borel measurable. Or, if $f: \mathbb{R} \to \mathbb{R}$ is measurable with respect to Lebesgue $\sigma$-algebra, we say $f$ is Lebesgue measurable.

Here are some examples.

click to expand

$\color{green}{\mathbf{Example\ 1.}}$ Suppose $f$ is real-valued and identically constant. Then $f^{-1} \left( (a, \infty) \right)$ for all $a \in \mathbb{R}$ is either $\emptyset$ or $X$, therefore $f$ is measurable.

$\color{green}{\mathbf{Example\ 2.}}$ Let

\[\begin{aligned} f(x) = \begin{cases} 1 & \quad \text{ if } x \in A \\ 0 & \quad \text{ otherwise } \end{cases} \end{aligned}\]

Then $f^{-1} \left( (a, \infty) \right)$ for all $a \in \mathbb{R}$ is either $\emptyset$, $A$, or $X$, therefore $f$ is measurable if and only if $A \in \mathcal{A}$.

$\color{green}{\mathbf{Example\ 3.}}$ Let $X = \mathbb{R}$ with the Borel $\sigma$-algebra, i.e. $\mathcal{A} = \mathcal{B}$ and $f(x) = x$. Then $f^{-1} \left( (a, \infty) \right)$ is $(a, \infty)$ for all $a \in \mathbb{R}$, therefore $f$ is measurable.

Algebraic properties of mesurable functions

Not suprisingly, measurable functions are closed under some basic operations:

$\color{red}{\mathbf{Thm.}}$ Algebraic properties of measurable functions
Let $c \in \mathbb{R}$. If $f$ and $g$ are measurable real-valued functions, then so are

1. $f + g$
2. $-f$, $cf$
3. $fg$
4. $\frac{1}{f}$, if we further assume $f (x) \neq 0$ for all $x \in X$

$\color{red}{\mathbf{Proof.}}$

(1) If $f(x) + g(x) < a$, $f(x) < a - g(x)$, and there exists a rational $r \in \mathbb{Q}$ such that $f(x) < r < a - g(x)$. Hence

\[\begin{aligned} \{ x \mid f(x) + g(x) < a \} = \bigcup_{r \in \mathbb{Q}} \left( \{ x \mid f(x) < r \} \cap \{ x \mid g(x) < a - r \} \right) \in \mathcal{A} \end{aligned}\]

(2) Since \(\{ x \mid - f(x) > a \} = \{ x \mid f(x) < - a \} \in \mathcal{A}\), done.

If $c > 0$, then \(\{ x \mid cf(x) > a \} = \{ x \mid f(x) > a / c \} \in \mathcal{A}\) shows $cf$ is measurable. If $c = 0$, $cf = 0$ is trivially measurable. If $c < 0$, then \(\{ x \mid cf(x) > a \} = \{ x \mid f(x) < a / c \} \in \mathcal{A}\), which is measurably by equivalent definition.

(3) Note that $f^2$ is measurable: for $a < 0$, \(\{ x \mid f(x)^2 > a \} = X\) while for $a \geq 0$,

\[\begin{aligned} \{ x \mid f(x)^2 > a \} = \{ x \mid f(x) > \sqrt{a} \} \cup \{ x \mid f(x) < -\sqrt{a} \} \in \mathcal{A} \end{aligned}\]

Then, the measurability of $fg$ follows from $fg = \frac{1}{2}[(f + g)^2 - f^2 - g^2]$.

(4) Since $\frac{1}{f(x)} = \frac{1}{f(x)}^+ - \frac{1}{f(x)}^-$, we can assume that $f(x) > 0$ without loss of generality.

Note that

\[\begin{aligned} \{ x : \frac{1}{f(x)} > a \} = \begin{cases} \emptyset & \in \mathcal{A} & \quad a < 0 \\ X & \in \mathcal{A} & \quad a = 0 \\ \{ x : f(x) < \frac{1}{a} \} & \in \mathcal{A} & \quad a > 0 \\ \end{cases} \end{aligned}\]

Thus the reciprocal of measurable $f$ is clearly measurable.

\[\tag*{$\blacksquare$}\]

Supremum and infimum of measurable functions

It is obvious to show that maximum and minimum measurable functions are also measurable:

$\color{red}{\mathbf{Thm.}}$ max and min of measurable function
If $f$ and $g$ are measurable real-valued functions, then so are $\text{max}(f, g)$, $\text{min}(f, g)$.

$\color{red}{\mathbf{Proof.}}$

The equality

\[\begin{aligned} \{ x \mid \text{max}(f(x), g(x)) > a \} = \{ x \mid f(x) > a \} \cup \{ x \mid g(x) > a \} \end{aligned}\]

proves that $\text{max}(f, g)$ is measurable. The result for $\text{min}(f, g)$ follows from $\text{min}(f, g) = \text{max}(-f, -g)$. \(\tag*{$\blacksquare$}\)

From this fact, we can show that positive and negative part of measurable functions are measurable:

$\color{blue}{\mathbf{Corollary.}}$ Let $f: X \to \mathbb{R}$ be a measurable function. Then, the positive and negative part of function $$ \begin{aligned} f^+ & = \text{max} ( f(x), 0 ) \\ f^- & = \text{max} ( -f(x), 0 ) \end{aligned} $$ are measurable. Obviously, if they are measurable, then $f = f^+ - f^-$ is also measurable.

These decompostions of functions will appear in the later concepts.

Furthermore, if exist, measurability is also closed under supremum, infimum, limit superior and limit inferior:

$\color{red}{\mathbf{Thm.}}$ Let $f_i$ be a measurable real-valued function for each $i$. Then, so are

1. $\text{sup}_i \; f_i$
2. $\text{inf}_i \; f_i$
3. $\text{lim sup}_{i \to \infty} \; f_i$
4. $\text{lim inf}_{i \to \infty} \; f_i$

if they are finite.

$\color{red}{\mathbf{Proof.}}$

(1) It is obvious to show that

\[\begin{aligned} \{ x \mid \underset{i}{\text{sup }} f_i (x) > a \} = \bigcup_{i=1}^\infty \{ x \mid f_i (x) > a \} \end{aligned}\]

Hence LHS is a countable union of Borel set, LHS is also a Borel set.

(2) Obviously,

\[\begin{aligned} \{ x \mid \underset{i}{\text{inf }} f_i (x) > a \} = \bigcap_{i=1}^\infty \{ x \mid f_i (x) > a \} \end{aligned}\]

(3), (4) The following equations prove the theorem:

\[\begin{aligned} \text{lim sup}_{i \to \infty} \; f_i & = \underset{j}{\text{inf }} \underset{i \geq j}{\text{sup }} f_i \\ \text{lim inf}_{i \to \infty} \; f_i & = \underset{j}{\text{sup }} \underset{i \geq j}{\text{inf }} f_i \end{aligned}\] \[\tag*{$\blacksquare$}\]

The finiteness condition is necessary because we are only talking about measurability of real-valued functions. If we discuss measurability of functions in the extended real number system $\bar{\mathbb{R}} = [-\infty, \infty]$, the assumption can be relieved.

$\color{blue}{\mathbf{Corollary.}}$ Let $\{ f_i \}$ be a sequence of measurable $\bar{\mathbb{R}}$-valued. Then, the following functions are all measurable:

1. $\text{sup}_i \; f_i$
2. $\text{inf}_i \; f_i$
3. $\text{lim sup}_{i \to \infty} \; f_i$
4. $\text{lim inf}_{i \to \infty} \; f_i$

Derivative of measurable functions

$\color{red}{\mathbf{Thm.}}$ Suppose $f: \mathbb{R} \to \mathbb{R}$ is differentiable at each point. Then, $f$ and $f^\prime$ are Borel measurable.

$\color{red}{\mathbf{Proof.}}$

Since $f$ is continuous, it is Borel measurable obviously.

Let $f_n (x) = f(x + \frac{1}{n})$. Then $f_n (x) is measurable and $f_n \to f$ due to continuity. Define

\[\begin{aligned} g_n (x) = \frac{f_n (x) - f(x)}{1/n} \end{aligned}\]

Note that $g_n \to f^\prime$ pointwisely for each point $x \in \mathbb{R}$. And $g_n$ is measurable for each $n \in \mathbb{N}$. Since $f^\prime (x) = \lim_{n \to \infty} g_n (x) = \underset{n}{\text{lim sup}} g_n (x)$ and does not diverge, it is Borel measurable too.

\[\tag*{$\blacksquare$}\]

Equivalent definitions for measurability

Recall that an inverse image commutes with set operations:

$\color{#bf1100}{\mathbf{Remark.}}$ Commutativity of inverse image
The following relations hold for the inverse image:

1. $f^{-1} \left( \bigcup_{i=1}^\infty A_i \right) = \bigcup_{i=1}^\infty f^{-1} (A_i)$
2. $f^{-1} \left( \bigcap_{i=1}^\infty A_i \right) = \bigcap_{i=1}^\infty f^{-1} (A_i)$
3. $\left( f^{-1} (A) \right)^c = f^{-1} (A^c)$
4. $f^{-1} (A - B) = f^{-1} (A) - f^{-1} (B)$

$\color{#bf1100}{\mathbf{Proof.}}$

(1)

\[\begin{aligned} f^{-1} \left( \bigcup_{i=1}^\infty A_i \right) & = \left\{ x \in X \; \middle| \; f(x) \in \bigcup_{i=1}^\infty A_i \right\} \\ & = \left\{ x \in X \; \middle| \; f(x) \in A_i \text{ for some } i = 1, 2, \cdots \right\} \\ & = \bigcup_{i=1}^\infty \left\{ x \in X \; \middle| \; f(x) \in \bigcup_{i=1}^\infty A_i \right\} \\ & = \bigcup_{i=1}^\infty f^{-1} (A_i). \\ \end{aligned}\]

(2)

\[\begin{aligned} f^{-1} \left( \bigcap_{i=1}^\infty A_i \right) & = \left\{ x \in X \; \middle| \; f(x) \in \bigcap_{i=1}^\infty A_i \right\} \\ & = \left\{ x \in X \; \middle| \; f(x) \in A_i \text{ for all } i = 1, 2, \cdots \right\} \\ & = \bigcap_{i=1}^\infty \left\{ x \in X \; \middle| \; f(x) \in \bigcap_{i=1}^\infty A_i \right\} \\ & = \bigcap_{i=1}^\infty f^{-1} (A_i). \\ \end{aligned}\]

(3)

1. $f^{-1} (A^c) \subseteq \left( f^{-1} (A) \right)^c$
   $$ \begin{aligned} x \in f^{-1} (A^c) \Rightarrow f(x) \in A^c \Rightarrow f(x) \notin A \Rightarrow x \notin f^{-1}(A) \end{aligned} $$
2. $\left( f^{-1} (A) \right)^c \subseteq f^{-1} (A^c)$
   $$ \begin{aligned} x \notin f^{-1} (A) \Rightarrow f(x) \notin A \Rightarrow f(x) \in A^c \Rightarrow x \in f^{-1} (A^c) \end{aligned} $$

(4) It naturally follows from (2) and (3).

\[\tag*{$\blacksquare$}\]

Therefore, we obtain an equivalent definition of measurability of function:

$\color{red}{\mathbf{Thm.}}$ Equivalent definition
A function $f: X \to \mathbb{R}$ is measurable if and only if $f^{-1} (B) \in \mathcal{B}$ for any Borel set $B \in \mathcal{B}$. Also, the following conditions are equivalent:

1. $\{ x: f(x) > a \} \in \mathcal{A}$ for all $a \in \mathbb{R}$
2. $\{ x: f(x) \leq a \} \in \mathcal{A}$ for all $a \in \mathbb{R}$
3. $\{ x: f(x) < a \} \in \mathcal{A}$ for all $a \in \mathbb{R}$
4. $\{ x: f(x) \geq a \} \in \mathcal{A}$ for all $a \in \mathbb{R}$

$\color{red}{\mathbf{Proof.}}$

Suppose $f^{-1} (B) \in \mathcal{B}$ for any Borel set $B \in \mathcal{B}$. Since $(a, \infty)$ is also a Borel set for any $a \in \mathbb{R}$, it implies $f$ is measurable.

Suppose $f$ is measurable. Let $\mathcal{B}$ be the Borel $\sigma$-algebra on $\mathbb{R}$ and \(\mathcal{C} = \{ B \subset f^{-1} (B) \in \mathcal{B} \}\).

We show that $\mathcal{C}$ is a $\sigma$-algebra that contains $(a, \infty)$ for every real $a$ that implies $\mathcal{C}$ contains $\sigma$-algebra generated by $(a, \infty)$, $\mathcal{B}$.

If $B_1, B_2, \dots \in \mathcal{B}$, then since

\[\begin{aligned} f^{-1}(\bigcup_{i=1}^\infty B_i) = \bigcup_{i=1}^\infty f^{-1}(B_i) \in \mathcal{A} \end{aligned}\]

we have that $\mathcal{C}$ is closed under countable unions. Similarly, $\mathcal{C}$ is closed under countable intersections and complements, therefore $\mathcal{C}$ is $\sigma$-algebra. Since $f$ is measurable, $\mathcal{C}$ contains $(a, \infty)$ for every $a \in \mathbb{R}$.

The remaining propositions are obvious. The equivalence of (1) and (2), and of (3) and (4) follow from taking complements and $\mathcal{A}$ is $\sigma$-algebra. And, if $f$ is measurable, since $\mathcal{A}$ is a $\sigma$-algebra,

\[\begin{aligned} \{ x: f(x) \geq a \} = \bigcap_{n=1}^\infty \{ x: f(x) > a - \frac{1}{n} \} \in \mathcal{A} \end{aligned}\]

shows that (4) holds if (1). Similarly we can show that (1) holds if (4). It completes the proof.

\[\tag*{$\blacksquare$}\]

Continuity and measurability

Considering the definition of a continuous function in a topology, the following relationship is naturally derived (with additional condition).

$\color{red}{\mathbf{Thm.}}$ Continuous function and measurable function
For measurable space $(X, \mathcal{A})$, if $X$ is a metric space, $\mathcal{A}$ contains all the open sets, and $f: X \to \mathbb{R}$ is continuous, then $f$ is measurable.

$\color{red}{\mathbf{Proof.}}$

Since $f$ is continuous, $f^{-1} (O)$ is open if $O$ is open. And since $(a, \infty)$ is open, \(\{ x : f(x) > a\} = f^{-1} ((a, \infty))\) is also open. Since $\mathcal{A}$ contains all the open sets, $f$ is measurable.

\[\tag*{$\blacksquare$}\]

$\color{blue}{\mathbf{Corollary.}}$ All continuous functions are Borel measurable.

Monotonicity and measurability

The same is true for increasing functions on $\mathbb{R}$:

$\color{red}{\mathbf{Thm.}}$ Monotone function and measurable function
If $f: \mathbb{R} \to \mathbb{R}$ is monotone, then $f$ is Borel measurable.

$\color{red}{\mathbf{Proof.}}$

Without loss of generality, suppose $f$ is increasing. (Otherwise, we may set $f = -g$ where $g$ is increasing.) Given $a \in \mathbb{R}$, let \(x_0 = \text{sup } \{ y \mid f(y) \leq a \}\).

If $f(x_0) \leq a$, then $f^{-1} ((a, \infty)) = (x_0, \infty)$, i.e Borel set. And $f^{-1} ((a, \infty)) = [x_0, \infty)$ is also a Borel set.

\[\tag*{$\blacksquare$}\]

Composition of mesurable functions

It is obvious that the compositions of measurable functions is measurable:

~

But, one should note that if $f, g: \mathbb{R} \to \mathbb{R}$ are Lebesgue measurable, it doesn’t follow that $f \circ g$ is Lebesgue measurable, even if $g$ is assumed continuous, so that $g$ is Borel measurable. The important thing is the measurability of $f$; if $f$ is either continuous or Borel measurable, instead of Lebesgue mesuarable, it is easy to show that $f \circ g$ is Lebesgue measurable.

$\color{red}{\mathbf{Thm.}}$ Composition of measurable functions
Let $f, g: \mathbb{R} \to \mathbb{R}$. Suppose $g$ is Lebesgue measurable.

1. $f$: continuous $\Rightarrow$ $f \circ g$ is Lebesgue measurable;
2. $f$: Borel measurable $\Rightarrow$ $f \circ g$ is Lebesgue measurable;
3. $f$: Lebesgue measurable $\Rightarrow$ $f \circ g$ is not need to be Lebesgue measurable.

$\color{red}{\mathbf{Proof.}}$

(1), (2)

Let any Borel set $B \in \mathcal{B}$ be given. Then, if $f$ is either Borel measurable or continuous (then, $g$ is Borel measurable by corollary above), $A = f^{-1} (B)$ will be Borel measurable. Since $g$ if Lebesgue measurable, then $g^{-1} (A)$ will be a Lebesgue measurable, proving that $f \circ g$ is Lebesgue measurable.

(3)

Let $F: [0, 1] \to [0, 1]$ be a Cantor function and define $G(x) = F(x) + x$. We already show that $G$ and $G^{-1}$ are continuous and there exists a non-measurable set $A$ contained in $G(C)$ and $B = G^{-1}(A)$ is Lebesgue measurable but not Borel measurable.

Set $f = \chi_B$ and $g = G^{-1}$. Then, it is clear that $g$ is Lebesgue measurable function since it is continuous and Lebesgue $\sigma$-algebra contains every open set. Also, one can easily show that $\chi_B$ is Lebesgue measurable as $B$ is Lebesgue measurable. But $\chi_B \circ G^{-1}$ is not Lebesgue measurable since

\[\begin{aligned} \{x : \chi_B \circ G^{-1} (x) > \frac{1}{2} \} = \{ x: G^{-1}(x) \in B \} = A \end{aligned}\]

where $A$ is not Lebesgue measurable.

\[\tag*{$\blacksquare$}\]

Approximation of measurable functions

Simple function

We now introduce some functions that are the building blocks for the integration theory. Let $(X, \mathcal{A})$ be a measurable space.

$\color{blue}{\mathbf{Definition.}}$ Characteristic & Simple function
If $E \in \mathcal{A}$, define the characteristic function, or indicator function of $E$ by $$ \begin{aligned} \chi_E (x) = \begin{cases} 1, \quad & x \in E; \\ 0, \quad & x \notin E. \end{cases} \end{aligned} $$ A simple function $s$ is a function of the form $$ \begin{aligned} s(x) = \sum_{i=1}^n a_i \chi_{E_i} (x) \end{aligned} $$ for real numbers $a_i$ and measurable sets $E_i$.

$\color{#bf1100}{\mathbf{Remark.}}$ $\chi_E$ is measurable if and only if $E \in \mathcal{A}$.

$\color{red}{\mathbf{Thm.}}$ Simple function approximation
Suppose $f$ is a non-negative and measurable function. Then there exists a sequence of non-negative measurable simple functions $s_n$ increasing pointwisely to $f$. If $f$ is bounded, then $s_n$ increasing uniformly to $f$.

$\color{red}{\mathbf{Proof.}}$

Let

\[\begin{aligned} A_{in} = \{ x: (i-1) / 2^n \leq f(x) < i / 2^n \} = f^{-1} \left( \left[ \frac{i-1}{2^n}, \frac{i}{2^n} \right) \right) \end{aligned}\]

and

\[\begin{aligned} B_{n} = \{ x: f(x) \geq n \} = f^{-1} \left( \left[n, \infty \right) \right) \end{aligned}\]

for each $n = 1, 2, \dots$ and $i = 1, 2, \cdots, n \cdot 2^n$. Then, define

\[\begin{aligned} s_n = \sum_{i=1}^{n 2^n} \frac{i - 1}{2^n} \chi_{A_{in}} + n \chi_{B_{n}}. \end{aligned}\]

The formula is a bit messy in print but easily understood graphically; for given step $n$, we just divide $[0, n]$ contained in the range of function into $n$ portions:

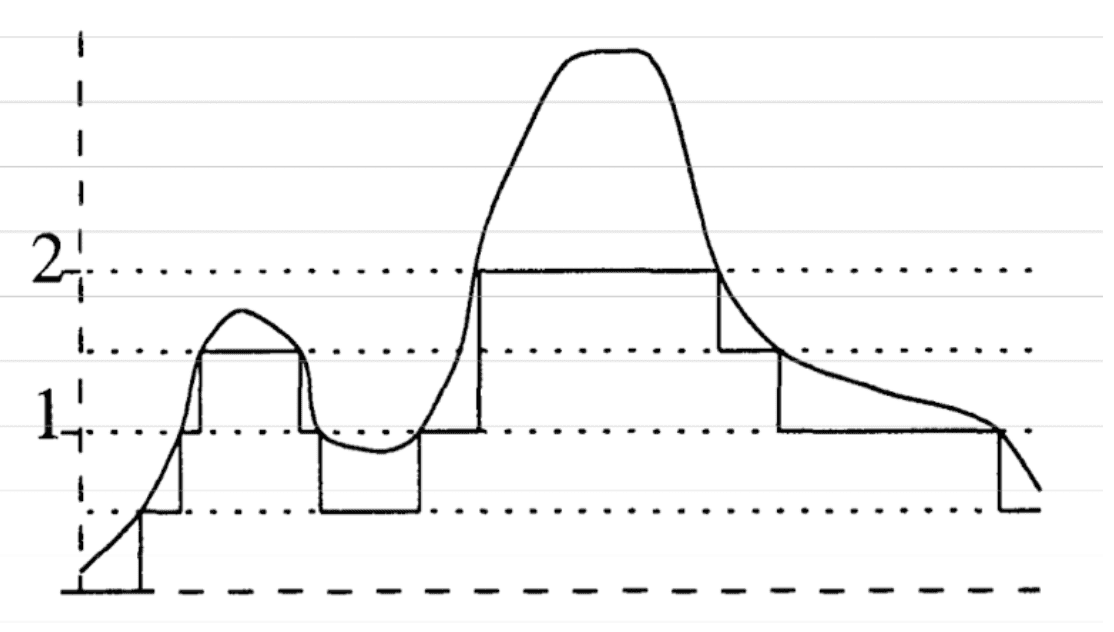
$\mathbf{Fig\ 1.}$ The function $s_2$ (source: Folland, Real Analysis)

In words, $s_n (x) = n$ if $f(x) \geq n$. If $f(x)$ is between $(i - 1) / 2^n$ and $i / 2^n$ for $i / 2^n \leq n$, we let $s_n (x) = (i - 1) / 2^n$.

Now, it is easy to show that $s_n \leq s_{n+1}$ for all $n$, and $s_n \to f$ pointwisely. Also, if $f$ is bounded, there exists $n_0 \in \mathbb{N}$ such that $f \leq n_0$. Then, for any $x$ in the domain of $f$, it satisfies that $0 \leq f - s_{n} \leq 2^{-n}$ for all $n \geq n_0$. The result therefore follows.

\[\tag*{$\blacksquare$}\]

Borel measurable functions

For any Lebesgue measurable $f: \mathbb{R} \to \mathbb{R}$, we can almost everywhere approximate $f$ with Borel measurable $g$. In other words, every Lebesgue measurable is almost Borel measurable.

$\color{red}{\mathbf{Thm.}}$ If $f: \mathbb{R} \to \mathbb{R}$ is Lebesgue measurable, there exists a Borel measurable function $g$ such that $f = g$ a.e.

$\color{red}{\mathbf{Proof.}}$

Without loss of generality, we may assume that $f$ is non-negative. Then, from $f = f^+ - f^-$ and Borel measurable $g = g^+ - g^-$, $f=g$ a.e.

For each $i = 1, 2, \cdots$ and $n \in \mathbb{N}$, since $f$ is Lebesgue measurable we can find $G_\delta$ set $B_{in}$ and $F_\sigma$ set $A_{in}$ with $m (B_{in} - A_{in}) = 0$ such that

\[\begin{aligned} A_{in} \subset f^{-1} \{ [\frac{i-1}{2^n}, \frac{i}{2^n}) \} \subset B_{in}. \end{aligned}\]

Set $C_n = \bigcup_{i=1}^\infty B_{in} - A_{in}$. Then, $C_n$ has a measure zero. Let \(A^{\prime}_{in} = A_{in} - C_n\), and construct

\[\begin{aligned} s_n (x) = \sum_{i=1}^\infty \frac{i-1}{2^n} \chi_{A^{\prime}_{in}} (x). \end{aligned}\]

• $s_n$ is well-defined as $A^{\prime}_{in}$ are pairwise disjoint.
• $s_n$ is Borel measurable as $A^{\prime}_{in}$ is a Borel set.

Then, for any $x \in \bigcup_{i=1}^\infty A^{\prime}_{in} = C_n^c$, we have

\[\begin{aligned} | s_n(x) - f(x) | < \frac{1}{2^n} \end{aligned}\]

therefore $f (x) = \lim_{n \to \infty} s_n (x)$ for all $x$ in $\bigcap_{n = 1}^\infty C_n^c$.

Combining these facts, we define Borel measurable $g$ as follows:

\[\begin{aligned} g (x) = \begin{cases} \lim_{n \to \infty} s_n (x) & \quad \text{ if } x \in C \\ 0 & \quad \text{ if } x \notin C \end{cases} \end{aligned}\]

where $C = \bigcap_{n=1}^n C_n^c$. $g$ is Borel measurable since $s_n$ is Borel measurable for all $n \in \mathbb{N}$. Note that $m (C^c) = 0$ as $C_n$ has a measure zero for all $n \in \mathbb{N}$. Thus $f = g$ a.e.

\[\tag*{$\blacksquare$}\]

Lusin’s Theorem

With simple functon approximation, we can prove a theorem for Lebesgue measurable functions called Lusin’s theorem that every measurable function is almost continuous.

$\color{red}{\mathbf{Thm.}}$ Lusin's Theorem
Suppose $f: [0, 1] \to \mathbb{R}$ is Lebesgue measurable, $m$ is Lebesgue measure, and $\varepsilon > 0$. Then there exists a closed set $F \subset [0, 1]$ such that $m([0, 1] - F) < \varepsilon$ and the restriction of $f$ to $F$ is a continuous function on $F$.

$\color{red}{\mathbf{Proof.}}$

Let any $\varepsilon > 0$ be given. Without loss of generality, let us assume that $f$ is non-negative. Since $f = f^+ - f^-$ for arbitrary measurable function $f$, the result will follow: find $F^+$ and $F^-$ closed such that $m([0, 1] - F^+) < \varepsilon / 2$, $m([0, 1] - F^-) < \varepsilon/2$, and $f^+$ restricted to $F^+$ is continuous and similarly for $f^-$. Then $F = F^+ \cap F^-$ is the desired set.

The brief idea of proof is as follows:

1. Since we assumed non-negativity, we will approximate $f$ with simple functions $s_n$.
2. We can find closed sets $E_n$ contained in $[0,1]$ such that $m([0, 1] - E_n)$ is small and $s_n$ is continuous on $E_n$ for each $n$. Then all $s_n$ will be continuous on $E = \bigcap_{n=1}^\infty E_n$
3. To make $s_n$’s limit $f$ be continuous, we will find a way that ensure the uniformity of $s_n \to f$:
   • We can find a closed set $D$ in [0,1] such that $m([0, 1] - D)$ is small and $f$ restriction on $D$, $f \cdot \chi_D$ is bounded.

Let’s begin the proof by finding $D$. Notice that

\[\begin{aligned} \left[ 0, 1 \right] = \bigcup_{n = 1}^\infty \{ x : f(x) \leq n \} \end{aligned}\]

Hence,

\[\begin{aligned} 1 = m([0, 1]) = \lim_{n \to \infty} m( \{x : f(x) \leq n \} ) \end{aligned}\]

Therefore, we can choose $n$ such that \(m \left(\{ x : f(x) \leq n \}\right) \geq 1 - \frac{\varepsilon}{3}\). And, we can choose a closed set \(D \subset \{ x : f(x) \leq n \}\) such that

\[\begin{aligned} m \left( \{ x : f(x) \leq n \} - D \right) < \frac{\varepsilon}{3} \end{aligned}\]

Set $\widetilde{f} = f \cdot \chi_D$. Note that $\widetilde{f}$ is a Lebesgue measurable, non-negative, and bounded by $n$. By simple function approximation, there exists a sequence of simple functions ${ s_n }$ that converges uniformly to $\widetilde{f}$ on $[0, 1]$.

$\mathbf{Claim.}$ We can find closed sets $E_n \subset [0, 1]$ such that $m([0, 1] - E_n) < \frac{\varepsilon}{3} \cdot 2^{-n}$ and $s_n$ is continuous on $E_n$ for each $n \in \mathbb{N}$.

$\mathbf{Proof.}$

Assume that $f = \chi_A$ where $A$ is a Lebesgue measurable subset of $[0, 1]$. We can find a closed set $E$ and an open set $G$ such that

\[\begin{aligned} E \subset A \subset G, \quad \quad m (G - A) < \frac{\varepsilon}{2} \text{ and } m (A - E) < \frac{\varepsilon}{2} \end{aligned}\]

Note that $E$ is closed and bounded, so that it is compact. Let

\[\begin{aligned} \delta = \text{inf} \left\{ | x - y | : x \in E, y \in G^c \right\} \end{aligned}\]

As $E \cap G^c = \emptyset$, $E$ is compact, and $G^c$ is closed, it obviously holds that $\delta > 0$.

Let

\[\begin{aligned} g(x) = \left( 1 - \frac{d(x, E)}{\delta} \right)^+ \end{aligned}\]

where \(y^+ = \text{max}(y, 0)\) and \(d(x, E) = \text{inf} \{ \lvert x-y \rvert : y \in E \}\). Then

• $g$ is continuous
  $\mathbf{Proof.}$

  Since $\text{max}(f(x), 0) = \frac{1}{2} (f(x) + | f(x) |)$, it suffices to show that $d(x, E)$ is continuous. And we claim that $d(x, E)$ is uniformly continuous.

  
  

  Let any $\varepsilon > 0$ be given. Then, let $x, y$ be any points in $X$ that $| x - y | < \varepsilon$. Let $p$ be any point in $E$. Then, by triangular inequality,

  \[\begin{aligned} d(x, p) \leq d(x, y) + d(y, p). \end{aligned}\]

  By taking infimum twice:

  \[\begin{aligned} d(x, E) & \leq d(x, y) + d(y, p) \\ d(x, E) & \leq d(x, y) + d(y, E) \end{aligned}\]

  Hence

  \[\begin{aligned} d(x, E) - d(y, E) & \leq d(x, y) \end{aligned}\]

  Similarly, we can derive $d(y, E) - d(x, E) \leq d(x, y)$ by just interchaning $x$ and $y$.

  Thus,

  \[\begin{aligned} | d(y, E) - d(x, E) | \leq d(x, y) < \varepsilon \end{aligned}\]

  which shows that $d(x, E)$ is uniformly continuous.

  \[\tag*{$\blacksquare$}\]
• $0 \leq g(x) \leq 1$ for all $x \in [0, 1]$
• $g(x) = 1$ on $E$ and $g(x) = 0$ on $G^c$

Take $F = (E \cup G^c) \cap [0, 1]$. Then $m([0, 1] - F) \leq m(G - E) < \varepsilon$. Also, $f$ restricted to $F$ is continuous since $f = g$ on $F$.

With this result, suppose $f = \sum_{i=1}^M a_i \chi_{A_i}$ is simple, where each $A_i$ is measurable set of $[0, 1]$ and each $a_i \geq 0$. Choose $F_i$ closed such that $m([0, 1] - F_i) < \varepsilon/M$ and $\chi_{A_i}$ restricted to $F_i$ is continuous.

If we let $F = \bigcap_{i=1}^M F_i$, then $F$ is closed, $m([0, 1] - F) < \varepsilon$, and $f$ restricted to $F$ is continuous.

\[\tag*{$\blacksquare$}\]

Then, if we set $E = \bigcap_{n=1}^\infty E_n$, $s_n$ is continuous for each $n$ on $E$. Since $\widetilde{f}$ is the uniform limit of $s_n$, $\widetilde{f}$ is continuous on $E$ clearly. Furthermore, $E$ is closed and

\[\begin{aligned} m\left([0, 1] - E \right) = m \left( \bigcup_{n=1}^\infty \left( [0, 1] - E_n \right) \right) \leq \sum_{n=1} m \left([0, 1] - E_n \right) < \frac{\varepsilon}{3} \end{aligned}\]

Set $F = D \cap E$. Then $F$ is closed, $f = \widetilde{f}$ on $F$. As $\widetilde{f}$ is continuous on $E$, $f$ is continuous on $F$. In addition,

\[\begin{aligned} m( [0, 1] - F) & = m( [0, 1] - D \cap E) \\ & \leq m( [0, 1] - D) + m( [0, 1] - E) \\ & \leq m \left([0, 1] - \{ x : f(x) \geq n \} \right) + m \left( \{ x : f(x) \geq n \} - D \right) \\ & \quad + m( [0, 1] - E ) \\ & < \frac{\varepsilon}{3} + \frac{\varepsilon}{3} + \frac{\varepsilon}{3} = \varepsilon \end{aligned}\] \[\tag*{$\blacksquare$}\]

Although we considered $[0, 1]$ only, it can be naturally extended to $[a, b]$. Also it is very pretty but usually other methods are better for solving problems. The next example will illustrate why this is a less useful theorem than at first glance.

https://mathworld.wolfram.com/MeasurableFunction.html https://iseulbee.com/archives/measure-integral-measurable-functions/ https://byjus.com/maths/measurable-functions/

Reference

[1] Richard F. Bass, Real Analysis for Graduate Students, Version 4.3
[2] Folland, Gerald B. Real analysis: modern techniques and their applications. Vol. 40. John Wiley & Sons, 1999.
[3] Wikipedia, Measurable space
[4] Demystifying the Caratheodory Approach to Measurability
[5] Show that every point of cantor set is a limit point
[6] Wikiepedia, Pre-measure