[RL] Distributional Control

Preliminary: Value Iteration

In classical reinforcement learning, the Bellman equation provides a simple equation for computing optimal state and state-action value function \(V^*\) and \(Q^*\):

\[V^* (\mathbf{s}) = \max_{\mathbf{a} \in \mathcal{A}} Q^* (\mathbf{s}, \mathbf{a}) Q^* (\mathbf{s}, \mathbf{a}) = r (\mathbf{s}, \mathbf{a}) + \gamma \mathbb{E}_{\mathbf{s}^\prime \sim \mathbb{P} (\cdot \vert \mathbf{s}, \mathbf{a})} \left[\max_{\mathbf{a}^\prime \in \mathcal{A}} Q^* (\mathbf{s}^\prime, \mathbf{a}^\prime) \right]\]

The dynamic programming, particularly value iteration finds the solution of these equations by iteratively applying the Bellman optimality operator $\mathcal{T}^*$:

\[(T^* Q) (\mathbf{s}, \mathbf{a}) = \mathbb{E}_\pi [r (\mathbf{s}_t, \mathbf{a}_t) + \gamma \max_{\mathbf{a}^\prime \in \mathcal{A}} Q( \mathbf{s}_{t+1}, \mathbf{a}^\prime ) \vert \mathbf{s}_t = \mathbb{s}, \mathbf{a}_t = \mathbf{a}]\]

Recall that the contractive nature of Bellman optimality operator ensures the convergence of algorithm within finite number of iterations:

$\color{red}{\mathbf{Theorem.}}$ $\gamma$-contractivity of $\mathcal{T}^*$
The Bellman optimality operator $\mathcal{T}^*$ is a contraction in $L^\infty$ norm with modulus $\gamma$: $$ \Vert \mathcal{T}^* Q - \mathcal{T}^* Q^\prime \Vert_\infty \leq \gamma \Vert Q - Q^\prime \Vert_\infty. $$

$\color{red}{\mathbf{Proof.}}$

For $f_1, f_2 : \mathcal{A} \to \mathbb{R}$, it can be easily shown that:

\[\vert \max_{\mathbf{a} \in \mathcal{A}} f_1 (\mathbf{a}) - \max_{\mathbf{a} \in \mathcal{A}} f_2 (\mathbf{a}) \vert \leq \max_{\mathbf{a} \in \mathcal{A}} \vert f_1 (\mathbf{a}) - f_2 (\mathbf{a}) \vert\]

Then for $Q, Q^\prime$, fix arbitrary $\mathbf{s} \in \mathcal{S}$ and $\mathbf{a} \in \mathcal{A}$. By linearity of expectations, we have:

\[\begin{aligned} \vert (\mathcal{T}^* Q) ( \mathbf{s}, \mathbf{a} ) - (\mathcal{T}^* Q^\prime) ( \mathbf{s}, \mathbf{a} ) \vert & = \gamma \Bigl\lvert \mathbb{E}_\pi [ \max_{\mathbf{a}^\prime \in \mathcal{A}} Q (\mathbf{s}_{t+1}, \mathbf{a}^\prime) - \max_{\mathbf{a}^\prime \in \mathcal{A}} Q^\prime (\mathbf{s}_{t+1}, \mathbf{a}^\prime) \vert \mathbf{s}_t = \mathbf{s}, \mathbf{a}_t = \mathbf{a} ] \Bigr\rvert \\ & \leq \gamma \mathbb{E}_\pi \left[ \Bigl\lvert \max_{\mathbf{a}^\prime \in \mathcal{A}} Q (\mathbf{s}_{t+1}, \mathbf{a}^\prime) - \max_{\mathbf{a}^\prime \in \mathcal{A}} Q^\prime (\mathbf{s}_{t+1}, \mathbf{a}^\prime) \Bigr\rvert \vert \mathbf{s}_t = \mathbf{s}, \mathbf{a}_t = \mathbf{a} \right] \\ & \leq \gamma \mathbb{E}_\pi \left[ \max_{\mathbf{a}^\prime \in \mathcal{A}} \Bigl\lvert Q (\mathbf{s}_{t+1}, \mathbf{a}^\prime) - Q^\prime (\mathbf{s}_{t+1}, \mathbf{a}^\prime) \Bigr\rvert \vert \mathbf{s}_t = \mathbf{s}, \mathbf{a}_t = \mathbf{a} \right] \\ & \leq \gamma \max_{\mathbf{s}^\prime, \mathbf{a}^\prime \in \mathcal{S} \times \mathcal{A}} \Bigl\lvert Q (\mathbf{s}^\prime, \mathbf{a}^\prime) - Q^\prime (\mathbf{s}^\prime, \mathbf{a}^\prime) \Bigr\rvert \\ & = \gamma \Vert Q - Q^\prime \Vert_\infty. \end{aligned}\] \[\tag*{$\blacksquare$}\]

For any initial value function estimate $Q_0$ be given and construct a sequence by

\[Q_{k+1} = \mathcal{T}^* Q_k \text{ where } (T^* Q) (\mathbf{s}, \mathbf{a}) = \mathbb{E}_\pi [r (\mathbf{s}_t, \mathbf{a}_t) + \gamma \\max_{\mathbf{a}^\prime \in \mathcal{A}} Q( \mathbf{s}_{t+1}, \mathbf{a}^\prime ) \vert \mathbf{s}_t = \mathbb{s}, \mathbf{a}_t = \mathbf{a}]\]

By $\gamma$-contractivity and Banach fixed point theorem, $Q^*$ is the unique convergence point of this sequence.

Distributional Bellman Optimality Operator

In distributional settings, since it is impossible to directly maximize the distribution, we instead defined the operator using greedy selection rule $\mathcal{G}$:

$\color{blue}{\mathbf{Definition.}}$ Greedy Selection Rule $\mathcal{G}$
A greedy selection rule is a mapping $\mathcal{G}: \mathbb{R}^{\mathcal{S} \times \mathcal{A}} \to \Pi$ such that for any state-action value $Q \in \mathbb{R}^{\mathcal{S} \times \mathcal{A}}$, $\mathcal{G} (Q)$ is greedy with respect to $Q$: $$ \mathcal{G}(Q) (\mathbf{a} \vert \mathbf{s}) > 0 \implies Q (\mathbf{s}, \mathbf{a}) = \max_{\mathbf{a}^\prime \in \mathcal{A}} Q (\mathbf{s}, \mathbf{a}^\prime) $$ In distributional setting, for $\eta \in \mathscr{P} (\mathbb{R})^{\mathcal{S} \times \mathcal{A}}$: $$ \mathcal{G}(\eta) = \mathcal{G}(Q_\eta) $$ where $Q_\eta$ is the induced state-action value function: $$ Q_\eta (\mathbf{s}, \mathbf{a}) = \mathbb{E}_{Z \sim \eta (\mathbf{s}, \mathbf{a})} [Z] $$

With the greedy selection rule, we can view the Bellman optimality operator $\mathcal{T}^*$ as the Bellman expectation operator $\mathcal{T}^\pi$ with $\pi = \mathcal{G}(Q)$. Analogously, in the distributional setting, the distributional Bellman optimality operator can be derived from $\mathcal{G}$:

$\color{blue}{\mathbf{Definition.}}$ Distributional Bellman optimality operator $\mathcal{T}^*$
The distributional Bellman optimality operator $\mathcal{T}^*$ is defined by: $$ \mathcal{T}^* \eta = \mathcal{T}^{\pi = \mathcal{G} (\eta)} \eta $$ where $\mathcal{T}^\pi$ is the distributional Bellman expectation operator: $$ (\mathcal{T}^\pi \eta) (\mathbf{s}, \mathbf{a}) = \mathbb{E}_{\pi} [ (b_{R, \gamma})_* (\eta) (\mathbf{S}^\prime, \mathbf{A}^\prime) \vert \mathbf{S} = \mathbf{s}, \mathbf{A} = \mathbf{a}] $$

Hence, $\mathcal{T}^*$ selects a policy at each state $\mathbf{s}$ that is greedy with respect to the expected values of $\eta_k (\mathbf{s}, \cdot)$ and computes the return distribution function by a single step of $\mathcal{T}^\pi$ using that policy.

Distributional Value Iteration

Distributional value iteration combines a greedy selection rule $\mathcal{G}$ and a projection $\Pi_\mathscr{F}$ regarding the representation $\mathscr{F}$ of the return distribution to compute an approximate optimal return function:

\[\eta_{k+1} = \Pi_\mathscr{F} \mathcal{T}^{\mathcal{G} (\eta_k)} \eta_k\]

Note that the greedy policy $\pi_k = \mathcal{G}(\eta_k)$ also requires the induced value function $Q_{\eta_k}$. In case of $\Pi_\mathscr{F}$ is mean-preserving, i.e., the mean of $\Pi_\mathscr{F}$ is equal to that of $\nu$ for any distribution $\nu$, we can say that:

\[Q_{\eta_{k + 1}} = \mathcal{T}^* Q_{\eta_k}\]

since $Q (\mathbf{s}, \mathbf{a})$ is the mean of $\eta(\mathbf{s}, \mathbf{a})$.

Convergence Theorem

Unlike $\mathcal{T}^\pi$, unfortunately, distributional optimality operators $\mathcal{T}^*$ are not contraction mappings in general:

$\color{#bf1100}{\mathbf{Proposition.}}$ $\mathcal{T}^*$ is not a contraction mapping
Let $d$ be a finite $c$-homogeneous probability metric and $\bar{d}$ be its supremum extension. Then, there exist a Markov decision process and two return-distribution functions $\eta$, $\eta^\prime$ such that for any greedy selection rule $\mathcal{G}$ and any discount factor $\gamma \in (0, 1]$: $$ \bar{d} (\mathcal{T}^* \eta, \mathcal{T}^* \eta^\prime) > \bar{d}(\eta, \eta^\prime) $$

$\color{#bf1100}{\mathbf{Proof.}}$

Consider the following MDP with two nonterminal states $x$, $y$ and two actions $a$, $b$. We can show that $\varepsilon$ can be chosed to make $\mathcal{T}^*$ to be non-contractive. See Section 7.4 of Bellemare et al. 2023.

$\mathbf{Fig\ 1.}$ Counterexample MDP (Bellemare et al. 2023)

\[\tag*{$\blacksquare$}\]

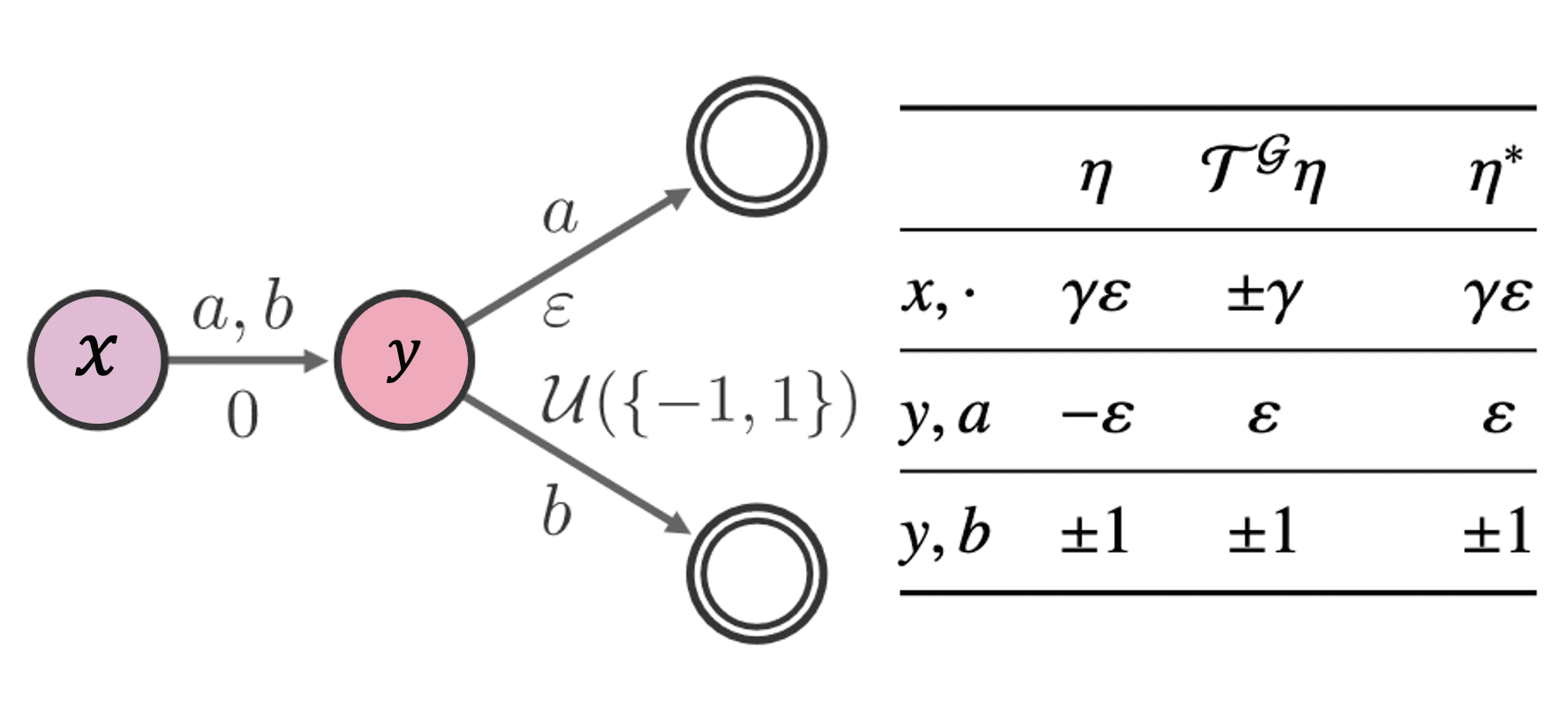
Therefore, we cannot directly appy the contraction mapping theory to the convergence theorem of $\mathcal{T}^*$. Instead, we can consider another approach using the concept of action gap.

$\color{blue}{\mathbf{Definition.}}$ Action Gap
Let $Q \in \mathbb{R}^{\mathcal{S} \times \mathcal{A}}$ be a state-action value function. The action gap at a state $\mathbf{s}$ is the difference between the highest-valued and second highest-valued actions: $$ \texttt{GAP}(Q, \mathbf{s}) = \min \{ Q (\mathbf{s}, \mathbf{a}^*) - Q (\mathbf{s}, \mathbf{a}) \vert \mathbf{a} \in \mathcal{A}, \mathbf{a}^* \neq \mathbf{a}, Q (\mathbf{s}, \mathbf{a}^*) = \max_{\mathbf{a}^\prime \in \mathcal{A}} Q (\mathbf{s}, \mathbf{a}^\prime) \} $$ And the action gap of $Q$ is defined as the smallest gap over all states: $$ \texttt{GAP}(Q) = \min_{\mathbf{s} \in \mathcal{S}} \texttt{GAP}(Q, \mathbf{s}) $$ In the distributional setting, the action gap for a return function $\eta$ is defined with its induced state-action value: $$ \texttt{GAP}(\eta) = \min_{\mathbf{s} \in \mathcal{S}} \texttt{GAP}(Q_\eta, \mathbf{s}) \text{ where } Q_\eta (\mathbf{s}, \mathbf{a}) = \mathbb{E}_{Z \sim \eta (\mathbf{s}, \mathbf{a})} [Z] $$

Note that \(\texttt{GAP}(Q^*) = 0\) implies that there are at least two optimal policies at a given state. However, in case of \(\texttt{GAP}(Q^*) > 0\), e.g., an optimal policy \(\pi^*\) is unique, we can guarantee the convergence of distributional value iteration regarding the Wasserstein distance.

$\color{red}{\mathbf{Theorem.}}$ Convergence of Distributional Value Iteration
Let $p \in [1, \infty]$. Let $\mathcal{T}^*$ be the distributional Bellman optimality operator instantiated with a greedy selection rule $\mathcal{G}$. Suppose that there is a unique optimal policy $\pi^*$ and the reward distribution $\mathbb{P}_\mathcal{R} (\cdot \vert \mathbf{s}, \mathbf{a})$ is in the finite domain $\mathscr{P}_{W_p} (\mathbb{R})$ of $W_p$ for any $(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}$. $$ \mathscr{P}_{W_p} (\mathbb{R}) = \{ \nu \in \mathscr{P}(\mathbb{R}) \mid \mathbb{E}_{ Z \sim \nu } [\vert Z \vert^p ] < \infty \} $$ Under these conditions, for any initial return-distribution function $\eta \in \mathscr{P}$, the sequence of iterates defined by $$ \eta_{k + 1} = \mathcal{T}^* \eta_k $$ converges to $\eta^{\pi^*}$ with respect to the metric $\bar{W}_p$.

$\color{red}{\mathbf{Proof.}}$

As we assumed that there is a unique optimal policy \(\pi^*\), it must be that the action gap of $Q^*$ is strictly greater than zero. Therefore, fix \(\varepsilon = \frac{1}{2} \texttt{GAP} (Q^*)\). Recall that

\[Q_{\eta_{k+1}} = \mathcal{T}^* Q_{\eta_k}\]

Since the Bellman optimality operator $\mathcal{T}^*$ is a contraction in $L^\infty$ norm, there exists a $K_\varepsilon \in \mathbb{N}$ such that

\[\Vert Q_{\eta_k} - Q^* \Vert_\infty < \varepsilon \quad \forall k \geq K_\varepsilon.\]

For fixed arbitrary state $\mathbf{s}$, let \(\mathbf{a}^*\) be the optimal action in that state. Then, for any \(\mathbf{a} \neq \mathbf{a}^*\) and $k \geq K_\varepsilon$:

\[\begin{aligned} Q_{\eta_k} (\mathbf{s}, \mathbf{a}^*) & \geq Q^* (\mathbf{s}, \mathbf{A}^*) \\ & \geq Q^* (\mathbf{s}, \mathbf{a}) + \texttt{GAP}(Q^*) - \varepsilon \\ & > Q_{\eta_k} (\mathbf{s}, \mathbf{a}) + \texttt{GAP}(Q^*) - 2 \varepsilon \\ & = Q_{\eta_k} (\mathbf{s}, \mathbf{a}). \end{aligned}\]

Thus, the greedy action in state $\mathbf{s}$ after time $K_\varepsilon$ is the optimal action for that state. Thus, $\mathcal{G}(\eta_k) = \pi^*$ for $k \geq K_\varepsilon$ and

\[\eta_{k + 1} \mathcal{T}^{\pi^*} \eta_k \quad k \geq K_\varepsilon\]

We can treat $\eta_{K_\varepsilon}$ as a new initial condition and apply the distributional policy evaluation to conclude that $\eta_k \to \eta^{\pi^*}$.

\[\tag*{$\blacksquare$}\]

$\color{blue}{\mathbf{Corollary.}}$ Convergence of Distributional Value Iteration
Suppose that $\Pi_\mathscr{F}$ of the representation $\mathscr{F}$ of return distributions is a mean-preserving and there is a unique optimal policy $\pi^*$. Also, assume the closedness of finite domain $\mathscr{P}_d (\mathbb{R})^\mathcal{S}$: $$ \eta \in \mathscr{P}_d (\mathbb{R})^\mathcal{S} \implies \mathcal{T}^\pi, \Pi_\mathscr{F} \eta \in \mathscr{P}_d (\mathbb{R})^\mathcal{S} $$ If $\Pi_\mathscr{F}$ is a non-expansion in $\bar{W}_p$, then the above theorem implies that the sequence of distributional value iteration $$ \eta_{k+1} = \Pi_\mathscr{F} \mathcal{T}^* \eta_k $$ onverges to the fixed point $$ \hat{\eta}^{\pi^*} = \Pi_\mathscr{F} \mathcal{T}^{\pi^*} \hat{\eta}^{\pi^*} $$

Categorical Q-Learning

Using an arbitrary greedy selection rule $\mathcal{G}$, categorical Q-learning is defined by the update:

\[\eta (\mathbf{s}, \mathbf{a}) \leftarrow ( 1 - \lambda ) \eta (\mathbf{s}, \mathbf{a} ) + \lambda \sum_{\mathbf{a}^\prime \in \mathcal{A}} \mathcal{G}(\eta) (\mathbf{a}^\prime \vert \mathbf{s}^\prime) \cdot \left( \Pi_C (b_{r, \gamma})_* (\eta) (\mathbf{s}^\prime, \mathbf{a}^\prime) \right)\]

Since $\Pi_C$ is mean-preserving, its induced state-value function also follows the update:

\[\begin{aligned} Q_\eta (\mathbf{s}, \mathbf{a}) & \leftarrow ( 1 - \lambda ) Q_\eta (\mathbf{s}, \mathbf{a}) + \lambda \sum_{\mathbf{a}^\prime \in \mathcal{A}} \mathcal{G}(\eta) (\mathbf{a}^\prime \vert \mathbf{s}^\prime) \cdot \left( r + \gamma Q_\eta (\mathbf{s}^\prime, \mathbf{a}^\prime) \right) \\ & = ( 1 - \lambda ) Q_\eta (\mathbf{s}, \mathbf{a}) + \lambda \left( r + \gamma \max_{\mathbf{a}^\prime \in \mathcal{A}} Q_\eta (\mathbf{s}^\prime, \mathbf{a}^\prime) \right) \end{aligned}\]

References

[1] Marc G. Bellemare and Will Dabney and Mark Rowland, “Distributional Reinforcement Learning”, MIT Press 2023
[2] Rowland et al. “An Analysis of Categorical Distributional Reinforcement Learning”, PMLR 2018
[3] Bellemare et al. “A Distributional Perspective on Reinforcement Learning”, ICML 2017
[4] Rowland et al. “Statistics and Samples in Distributional Reinforcement Learning”, PMLR 2019