[RL] Conservative Q-Learning (CQL)

Motivation: Overestimation of values in unseen actions

The policy $\pi$ of value-based off-policy algorithms is trained to maximize Q-values. In an offline setting, this generally yield poor performance due to overestimated, optimistic value function estimates attributed by bootstrapping from out-of-distribution actions and overfitting. Recall that the general loss function of value-based off-policy RL is defined as follows for target policy $\pi$:

\[\texttt{General Offline RL: } \mathcal{J} (\theta) = \mathbb{E}_{(\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) \sim \mathcal{D}} \left[\left( r(\mathbf{s}, \mathbf{a}) + \gamma \mathbb{E}_{\mathbf{a}^\prime \sim \pi (\cdot \vert \mathbf{s})} [Q_\theta (\mathbf{s}^\prime, \mathbf{a}^\prime)] - Q_\theta (\mathbf{s}, \mathbf{a}) \right)^2 \right]\]

$\mathbf{Fig\ 1.}$ Overestimation of unseen actions when standard off-policy deep RL algorithms (e.g., SAC) (source: Aviral Kumar and Avi Singh)

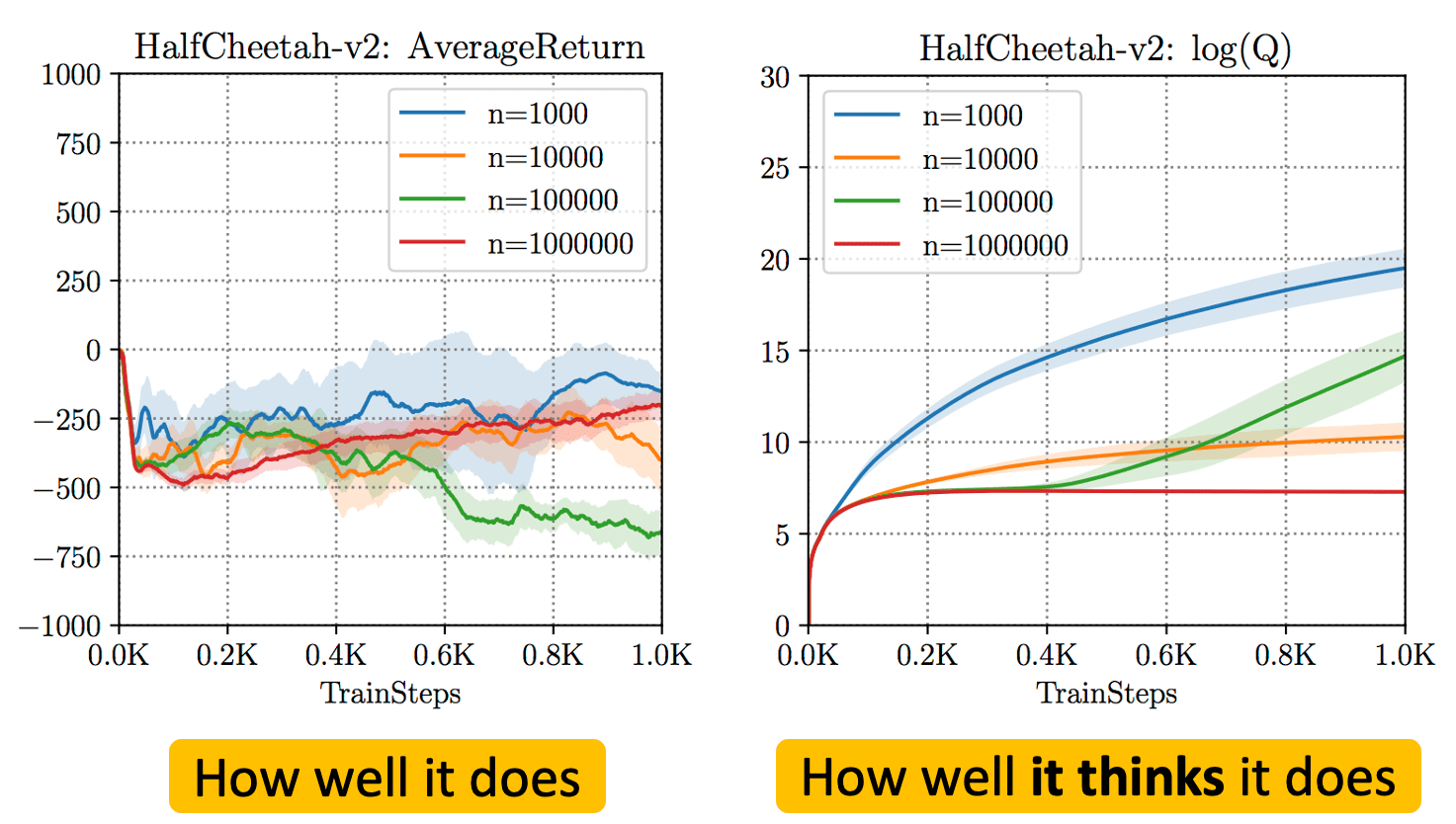
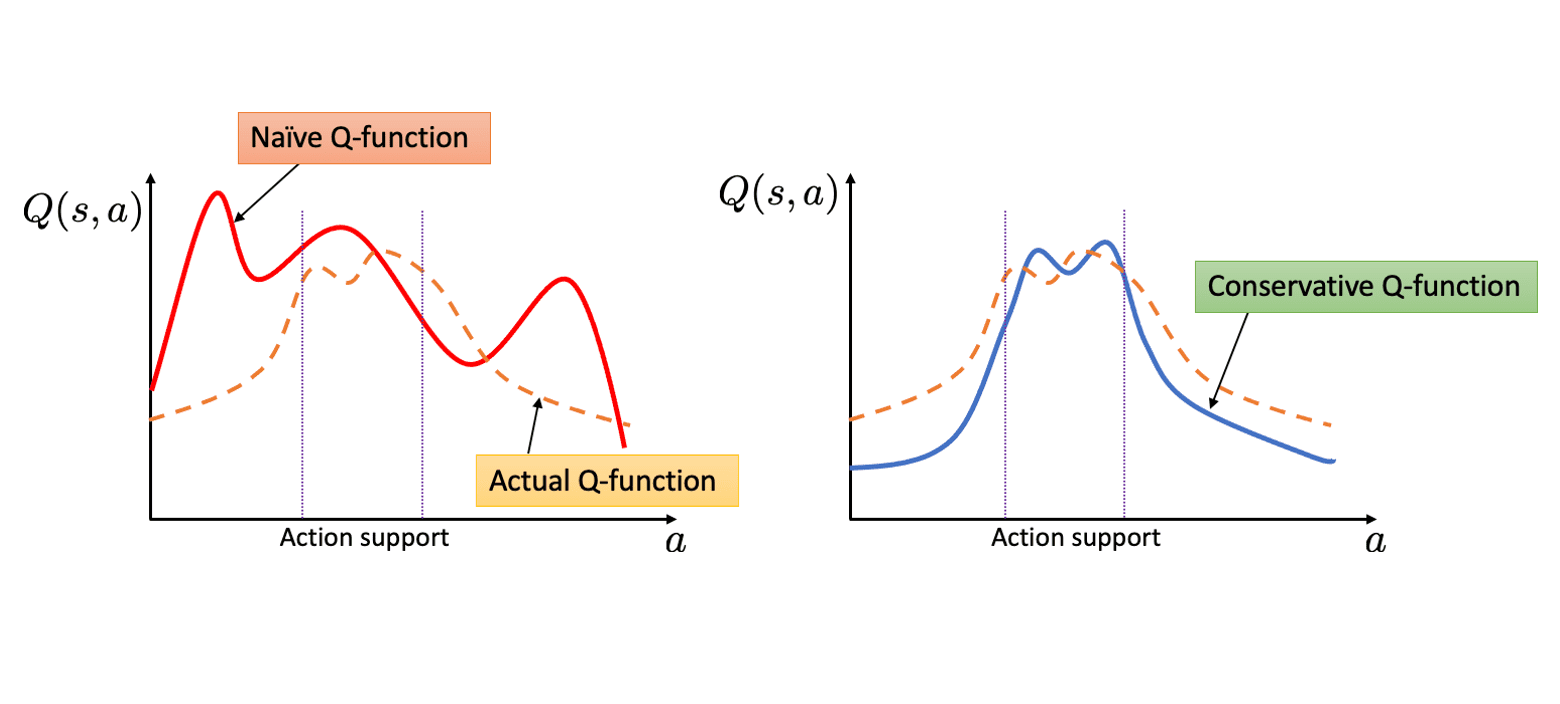
Instead, intuitively, by learning a conservative estimate of the value function that offers a lower bound on the true values, this overestimation problem can be mitigated. Conservative Q-Learning (CQL) simply learns such “conservative” Q-functions by just adding regularization terms $\mathcal{R}(\theta)$:

\[\texttt{Conservative Q-Learning: } \mathcal{L} (\theta) = \mathcal{J} (\theta) + \mathcal{R}(\theta)\]

where

\[\begin{aligned} \mathcal{R} (\theta) = & \max_{\mu} \mathbb{E}_{\mathbf{s} \sim \mathcal{D}, \mathbf{a} \sim \mu (\cdot \vert \mathbf{s})} [Q_\theta (\mathbf{s}, \mathbf{a})] \\ & - \mathbb{E}_{\mathbf{s} \sim \mathcal{D}, \mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} [Q_\theta (\mathbf{s}, \mathbf{a})] + \mathcal{R} (\mu) \end{aligned}\]

and $\mathcal{R} (\mu)$ is a regularization term for the policy $\mu (\mathbf{a} \vert \mathbf{s})$. It minimizes values under an appropriately chosen distribution $\mu (\cdot \vert \mathbf{s})$ that visits the unseen actions in $\mathcal{D}$ (that is, out-of-distribution of $\pi_\beta$), and then further tightening this bound by also incorporating a maximization term over the data distribution.

$\mathbf{Fig\ 2.}$ Learning conservative Q-functions (Aviral Kumar and Avi Singh)

Conservative Off-Policy Evaluation

Recall that the Bellman operator $\mathcal{B}^\pi$ is defined as:

\[\mathcal{B}^\pi Q = r + \gamma \mathcal{P}^\pi Q\]

where $\mathcal{P}^\pi$ is the transition matrix coupled with the policy:

\[\mathcal{P}^\pi Q(\mathbf{s}, \mathbf{a}) = \mathbb{E}_{\mathbf{s}^\prime \sim \mathbb{P}_\mathcal{S} (\cdot \vert \mathbf{s}, \mathbf{a}), \mathbf{a}^\prime \sim \pi (\cdot \vert \mathbf{s}^\prime)} [Q (\mathbf{s}^\prime, \mathbf{a}^\prime)]\]

However, since $\mathcal{D}$ typically does not contain all possible transitions $(\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime)$, the policy evaluation step actually uses an empirical Bellman operator $\hat{\mathcal{B}}^\pi$ that only backs up a single sample:

\[\hat{\mathcal{B}}^\pi Q (\mathbf{s}, \mathbf{a}) = r (\mathbf{s}, \mathbf{a}) + \gamma \mathbb{E}_{\mathbf{a}^\prime \sim \pi (\cdot \vert \mathbf{s}^\prime)} [Q(\mathbf{s}^\prime, \mathbf{a}^\prime)]\]

Note that if the target policy $\pi$ is an optimal policy, then Bellman operator $\mathcal{B}^\pi$ is equivalent to Bellman optimality operator $\mathcal{B}^*$:

\[\mathcal{B}^* Q (\mathbf{s}, \mathbf{a}) = r (\mathbf{s}, \mathbf{a}) + \gamma \mathbb{E}_{\mathbf{s}^\prime \sim \mathbb{P}_\mathcal{S} (\cdot \vert \mathbf{s}, \mathbf{a})} \left[ \max_{\mathbf{a}^\prime \in \mathcal{A}} Q (\mathbf{s}^\prime, \mathbf{a}^\prime) \right]\]

Therefore, in this post, we will focus on $\mathcal{B}^\pi$ (and $\hat{\mathcal{B}}^\pi$) for generality.

Learning Conservative Lower-bound Q-function

To learn conservative, lower-bound Q-function, the authors simply minimizes the expected Q-value under a particular distribution $\mu (\mathbf{a} \vert \mathbf{s})$ that visits unseen actions in $\mathcal{D}$ (that is, out-of-distribution of $\pi_\beta$):

\[\hat{Q}^{k + 1} \leftarrow \underset{Q}{\arg \min} \; \left( \alpha \underbrace{\mathbb{E}_{\mathbf{s} \sim \mathcal{D}, \mathbf{a} \sim \mu (\cdot \vert \mathbf{s})} [Q (\mathbf{s}, \mathbf{a})]}_{\textrm{Penalize large Q-values}} + \frac{1}{2} \underbrace{\mathbb{E}_{(\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) \sim \mathcal{D}} \left[ \left( Q (\mathbf{s}, \mathbf{a}) - \hat{\mathcal{B}}^\pi \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right)^2 \right]}_{\textrm{Standard Bellman error}} \right)\]

where $\vert r (\mathbf{s}, \mathbf{a}) \vert \leq R_{\max}$ and $\alpha > 0$ is the trade-off hyperparameters. And the resulting Q-function $\hat{Q}^\pi := \lim_{k \to \infty} \hat{Q}^k$, serves as a lower-bound of $Q^\pi$ at all $(\mathbf{s}, \mathbf{a})$ for sufficiently large $\alpha$:

$\color{red}{\mathbf{Theorem.}}$ Conservative Off-Policy Evaluation
For any $\mu (\mathbf{a} \vert \mathbf{s})$ with $\mathrm{supp} \; \mu \subset \mathrm{supp} \; \pi_\beta$, the following inequality holds for any $(\mathbf{s} \in \mathcal{D}, \mathbf{a})$ with probability $\geq 1 − \delta$: $$ \hat{Q}^\pi (\mathbf{s}, \mathbf{a}) \leq Q^\pi (\mathbf{s}, \mathbf{a}) - \alpha \left[ (I - \gamma \mathcal{P}^\pi)^{-1} \frac{\mu}{\pi_\beta} \right] (\mathbf{s}, \mathbf{a}) + \left[ (I - \gamma \mathcal{P}^\pi)^{-1} \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} \vert}} \right] (\mathbf{s}, \mathbf{a}). $$ for some constant $C_{r, \mathbb{P}_\mathcal{S}, \delta} > 0$. Therefore, if $\alpha$ is sufficiently large, then $\hat{Q}^\pi (\mathbf{s}, \mathbf{a}) \leq Q^\pi (\mathbf{s}, \mathbf{a})$ for any $(\mathbf{s} \in \mathcal{D}, \mathbf{a})$. Also, for large dataset $\vert \mathcal{D} \vert \gg 1$, any $\alpha > 0$ guarantees $\hat{Q}^\pi (\mathbf{s}, \mathbf{a}) \leq Q^\pi (\mathbf{s}, \mathbf{a})$, too.

$\mathbf{Proof.}$

To prove the theorem, we can always clamp the Q-values so that:

\[\left\vert \hat{Q}^k \right\vert \leq \frac{2 R_{\max}}{1- \gamma}\]

Note that the solution $Q$ of the update rule can be obtained by setting the derivative of the update equation to $0$:

\[\hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) = \hat{\mathcal{B}}^\pi \hat{Q}^k (\mathbf{s}, \mathbf{a}) - \alpha \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})}\]

Therefore, $\hat{Q}^{k+1} \leq \hat{\mathcal{B}}^\pi \hat{Q}^k$. To relate the empirical Bellman operator $\hat{\mathcal{B}^\pi}$ to the actual Bellman operator $\mathcal{B}^\pi$ that yields the true Q-value iterate of vanilla policy evaluation, we require the following concentration lemma:

$\color{green}{\mathbf{Lemma.}}$ Upper-bound of Sampling Error
Let $r$ be the empirical average reward obtained in the dataset when executing an action $\mathbf{a}$ at state $\mathbf{s}$: $$ r = \frac{1}{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert} \sum_{(\mathbf{s}_i, \mathbf{a}_i) \in \mathcal{D}} \mathbf{1}_{\mathbf{s}_i = \mathbf{s}, \mathbf{a}_i = \mathbf{a}} \cdot r(\mathbf{s}, \mathbf{a}) $$ and $\hat{\mathbb{P}}_\mathcal{S}$ be the empirical transition matrix. Assume that the following inequalities hold with high probability $\geq 1 - \delta$: $$ \begin{aligned} & \vert r - r (\mathbf{s}, \mathbf{a}) \vert \leq \frac{C_{r, \delta}}{\sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}} \\ & \left\Vert \hat{\mathbb{P}}_\mathcal{S} (\mathbf{s}^\prime \vert \mathbf{s}, \mathbf{a}) - \mathbb{P}_\mathcal{S} (\mathbf{s}^\prime \vert \mathbf{s}, \mathbf{a}) \right\Vert_1 \leq \frac{C_{\mathbb{P}_\mathcal{S}, \delta}}{\sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}} \end{aligned} $$ Then, the sampling error, i.e., the difference between the empirical Bellman operator and the actual Bellman operator, can be bounded as: $$ \left\vert \hat{\mathcal{B}}^\pi \hat{Q}^k - \mathcal{B}^\pi \hat{Q}^k \right\vert \leq \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}} $$ with some constant $C_{r, \mathbb{P}_\mathcal{S}, \delta} > 0$ for any $Q$ and $(\mathbf{s}, \mathbf{a}) \in \mathcal{D}$.

$\mathbf{Proof.}$

\[\begin{aligned} \left|\left(\hat{\mathcal{B}}^\pi \hat{Q}^k\right)-\left(\mathcal{B}^\pi \hat{Q}^k\right)\right| & =\left|(r-r(\mathbf{s}, \mathbf{a}))+\gamma \sum_{\mathbf{s}^{\prime}}\left(\hat{T}\left(\mathbf{s}^{\prime} \mid \mathbf{s}, \mathbf{a}\right)-T\left(\mathbf{s}^{\prime} \mid \mathbf{s}, \mathbf{a}\right)\right) \mathbb{E}_{\pi\left(\mathbf{a}^{\prime} \mid \mathbf{s}^{\prime}\right)}\left[\hat{Q}^k\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right]\right| \\ & \leq|r-r(\mathbf{s}, \mathbf{a})|+\gamma\left|\sum_{\mathbf{s}^{\prime}}\left(\hat{T}\left(\mathbf{s}^{\prime} \mid \mathbf{s}, \mathbf{a}\right)-T\left(\mathbf{s}^{\prime} \mid \mathbf{s}, \mathbf{a}\right)\right) \mathbb{E}_{\pi\left(\mathbf{a}^{\prime} \mid \mathbf{s}^{\prime}\right)}\left[\hat{Q}^k\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right]\right| \\ & \leq \frac{C_{r, \delta}+\gamma C_{T, \delta} 2 R_{\max } /(1-\gamma)}{\sqrt{|\mathcal{D}(\mathbf{s}, \mathbf{a})|}} . \end{aligned}\] \[\tag*{$\blacksquare$}\]

By the lemma, the following can be obtained with high probability $\geq 1 - \delta$:

\[\hat{Q}^{k + 1} (\mathbf{s}, \mathbf{a}) \leq \mathcal{B}^\pi \hat{Q}^k (\mathbf{s}, \mathbf{a}) - \alpha \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} + \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}}\]

Therefore, for the fixed point $\hat{Q}^\pi$, from the equation $(I - \gamma \mathcal{P}^\pi) Q^\pi = R$ and:

\[\hat{Q}^\pi - \mathcal{B}^\pi \hat{Q}^\pi = (I - \gamma \mathcal{P}^\pi) \hat{Q}^\pi - R\]

where $R$ is the reward function, we obtain:

\[\begin{gathered} \hat{Q}^\pi (\mathbf{s}, \mathbf{a}) \leq \mathcal{B}^\pi \hat{Q}^\pi (\mathbf{s}, \mathbf{a}) - \alpha \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} + \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}} \\ \Downarrow \\ \hat{Q}^\pi \leq (I - \gamma \mathcal{P}^\pi)^{-1} \left[ R - \alpha \frac{\mu}{\pi_\beta} + \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} \vert}} \right] \end{gathered}\]

This leads to the relationship in the theorem. Note that $\alpha$ can be chosen to cancel any potential overestimation incurred by \(\frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}}\):

\[\begin{gathered} \alpha \cdot \min_{\mathbf{s}, \mathbf{a}} \left[ \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \right] \geq \max_{\mathbf{s}, \mathbf{a}} \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}} \\ \Downarrow \\ \alpha \geq \max_{\mathbf{s}, \mathbf{a}} \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}} \cdot \max_{\mathbf{s}, \mathbf{a}} \left[ \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \right]^{-1} \end{gathered}\]

Also, if $\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert$ is sufficiently large such that \(\frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}, \mathbf{a}) \vert}} \approx 0\), lower bound holds for any $\alpha \geq 0$.

\[\tag*{$\blacksquare$}\]

Learning Conservative Lower-bound Value function

If we aim to estimate conservative lower-bound of $V^\pi (\mathbf{s})$ rather than $Q^\pi (\mathbf{s}, \mathbf{a})$, we can significantly refine this bound by pushing up Q-values that $(\mathbf{s}, \mathbf{a})$ are seen in $\mathcal{D}$, even if it leads to overestimation. And the following update rule minimizes Q-values for out-of-distribution actions while concurrently maximizing the expected Q-value on the dataset:

\[\begin{multline} \hat{Q}^{k+1} \leftarrow \underset{Q}{\arg\min} \; \alpha \cdot \left(\mathbb{E}_{\mathbf{s} \sim \mathcal{D}, \mathbf{a} \sim \mu(\mathbf{a} \vert \mathbf{s})} \left[ Q (\mathbf{s}, \mathbf{a}) \right] - \color{red}{\mathbb{E}_{\mathbf{s} \sim \mathcal{D}, \mathbf{a} \sim \pi_\beta (\mathbf{a} \vert \mathbf{s})} \left[Q(\mathbf{s}, \mathbf{a})\right]} \right) \\ + \frac{1}{2} \mathbb{E}_{\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime \sim \mathcal{D}}\left[\left(Q(\mathbf{s}, \mathbf{a}) - \hat{\mathcal{B}}^\pi \hat{Q}^{k} (\mathbf{s}, \mathbf{a}) \right)^2 \right]. \end{multline}\]

While the resulting Q-value $\hat{Q}^\pi$ may not serve as a point-wise lower-bound of $Q^\pi$, we have $\hat{V}^\pi (\mathbf{s}) = \mathbb{E}_\pi [\hat{Q}^\pi (\mathbf{s}, \mathbf{a})] \leq V^\pi (\mathbf{s})$, as demonstrated by the following theorem:

$\color{red}{\mathbf{Theorem.}}$ Tighter Lower-bound for $V^\pi$
Let $\hat{V}^\pi$ be the value of the policy uner the Q-function $\hat{Q}^\pi$: $$ \hat{V}^\pi (\mathbf{s}) = \mathbb{E}_{\mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} \left[ \hat{Q}^\pi (\mathbf{s}, \mathbf{a}) \right] $$ Then, $\hat{V}^\pi$ lower-bounds the true value $V^\pi$ obtained via exact policy evaluation for any $\mathbf{s} \in \mathcal{D}$ when $\mu = \pi$ such that: $$ \hat{V}^\pi (\mathbf{s}) \leq V^\pi (\mathbf{s}) - \alpha \left[ (I - \gamma \mathcal{P}^\pi)^{-1} \mathbb{E}_{\mathbf{a} \sim \pi} \left[ \frac{\pi}{\pi_\beta} - 1 \right] \right] (\mathbf{s}) + \left[ (I - \gamma \mathcal{P}^\pi)^{-1} \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} \vert}} \right] (\mathbf{s}). $$

$\mathbf{Proof.}$

To prove the theorem, we can always clamp the Q-values so that:

\[\left\vert \hat{Q}^k \right\vert \leq \frac{2 R_{\max}}{1- \gamma}\]

Note that the solution $Q$ of the update rule can be obtained by setting the derivative of the update equation to $0$:

\[\hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) = \hat{\mathcal{B}}^\pi \hat{Q}^k (\mathbf{s}, \mathbf{a}) - \alpha \left[ \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right]\]

Observe that for some $(\mathbf{s}, \mathbf{a})$ such that $\mu (\mathbf{a} \vert \mathbf{s}) < \pi_\beta (\mathbf{a} \vert \mathbf{s})$, we cannot guarantee that $\hat{Q}^{k +1}$ is a point-wise lower bound of $Q^{k + 1}$.

Instead, the value of the policy $\hat{V}^{k+1}$ is underestimated as we expected:

\[\hat{V}^{k + 1} (\mathbf{s}) = \mathbb{E}_{\mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] = \hat{\mathcal{B}}^\pi \hat{V}^k (\mathbf{s}) - \alpha \mathbb{E}_{\mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} \left[ \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right]\]

since we can show that \(\mathbb{E}_{\mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} \left[ \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right]\) is always positive when $\mu = \pi$:

\[\begin{aligned} \mathbb{E}_{\mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} \left[ \frac{\mu (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right] & = \sum_{\mathbf{a} \in \mathcal{A}} \pi (\mathbf{a} \vert \mathbf{s}) \left[ \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right] \\ & = \sum_{\mathbf{a} \in \mathcal{A}} (\pi (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s}) + \pi_\beta (\mathbf{a} \vert \mathbf{s})) \left[ \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right] \\ & = \sum_{\mathbf{a} \in \mathcal{A}} (\pi (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s})) \left[ \frac{\pi (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \right] + \sum_{\mathbf{a} \in \mathcal{A}} \pi_\beta (\mathbf{a} \vert \mathbf{s}) \left[ \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right] \\ & = \sum_{\mathbf{a} \in \mathcal{A}} \left[ \frac{(\pi (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s}))^2}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \right] + 0 \\ & \geq 0 \end{aligned}\]

This implies that each value iterate incurs some underestimation, $\hat{V}^{k+1} \leq \hat{\mathcal{B}}^\pi \hat{V}^k$.

By using upper-bound of sampling error in the lemma of the previous theorem, the following can be obtained with high probability $\geq 1 - \delta$:

\[\hat{V}^{k + 1} (\mathbf{s}) \leq \mathcal{B}^\pi \hat{V}^k (\mathbf{s}) - \alpha \mathbb{E}_{\mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} \left[ \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right] + \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}) \vert}}\]

Therefore, for the fixed point $\hat{V}^\pi$, from the equation $(I - \gamma \mathcal{P}^\pi) V^\pi = R$ and:

\[\hat{V}^\pi - \mathcal{B}^\pi \hat{V}^\pi = (I - \gamma \mathcal{P}^\pi) \hat{V}^\pi - R\]

where $R$ is the reward function, we obtain:

\[\begin{gathered} \hat{V}^\pi (\mathbf{s}) \leq \mathcal{B}^\pi \hat{V}^\pi (\mathbf{s}) - \alpha \mathbb{E}_{\mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} \left[ \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right] + \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} (\mathbf{s}) \vert}} \\ \Downarrow \\ \hat{V}^\pi \leq (I - \gamma \mathcal{P}^\pi)^{-1} \left[ R - \alpha \mathbb{E}_{\pi} \left[ \frac{\pi}{\pi_\beta} - 1 \right] + \frac{C_{r, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{(1 - \gamma) \sqrt{\vert \mathcal{D} \vert}} \right] \end{gathered}\]

This leads to the relationship in the theorem.

\[\tag*{$\blacksquare$}\]

Conservative Q-Learning

Due to fixed $\mu = \pi$, we should alternate between performing full off-policy evaluation for each policy iterate $\hat{\pi}^k$ and one step of policy improvement to obtain optimal policy, which can be computationally expensive. Instead, we could combine evaluation and improvement by choosing $\mu (\mathbf{a} \vert \mathbf{s})$ to approximate the policy that would maximize the current Q-function iterate for each iteration $k$:

\[\begin{multline} \hat{Q}^{k + 1} \leftarrow \underset{Q}{\arg \min} \; \color{red}{\max_\mu} \; \alpha \left(\mathbb{E}_{\mathbf{s} \sim \mathcal{D}, \mathbf{a} \sim \color{red}{\mu (\cdot \vert \mathbf{s})}} [ Q (\mathbf{s}, \mathbf{a}) ] - \mathbb{E}_{\mathbf{s} \sim \mathcal{D}, \mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} [ Q (\mathbf{s}, \mathbf{a}) ] \right) \\ + \frac{1}{2} \mathbb{E}_{(\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) \sim \mathcal{D}} \left[ \left( Q (\mathbf{s}, \mathbf{a}) - \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right)^2 \right] + \color{red}{\mathcal{R}(\mu)} \end{multline}\]

where $\pi_k$ is the policy iterate of true Q-learning, i.e., $Q^{k + 1} = \mathcal{B}^{\pi_k} Q^k$ and $\mathcal{R} (\mu)$ is the regularization term that controls the shape of $\mu$. Such online algorithm characterized by a particular choice of $\mathcal{R}(\mu)$ is termed Conservative Q-Learning $\texttt{CQL} (\mathcal{R})$.

$\mathbf{Fig\ 3.}$ The pseudocode of CQL (Kumar et al., 2020)

Variants of CQL

For regularization term, the authors considered $\mathcal{R} (\mu)$ to be the KL-divergence against a prior distribution $\rho (\mathbf{a} \vert \mathbf{s})$ which yields the optimal solution $\mu^*$:

\[\mu^* (\mathbf{a} \vert \mathbf{s}) \propto \rho (\mathbf{a} \vert \mathbf{s}) \exp (Q(\mathbf{s}, \mathbf{a}))\]

1. $\texttt{CQL}(\mathbb{H})$
   For an optimization problem of the form: $$ \begin{aligned} \max_{\mu} \; \mathbb{E}_{\mathbf{a} \sim \mu (\cdot \vert \mathbf{s})} [Q(\mathbf{s}, \mathbf{a})] + \mathbb{H} (\mu) \quad \text{ s.t. }\quad \sum_{\mathbf{a} \in \mathcal{A}} \mu (\mathbf{a} \vert \mathbf{s}) = 1 \end{aligned} $$ where $\mathbb{H}$ is an entropy: $$ \mathbb{H} (\mu) = \sum_{\mathbf{a} \in \mathcal{A}} \mu (\mathbf{a} \vert \mathbf{s}) \cdot \log \frac{1}{\mu (\mathbf{a} \vert \mathbf{s})} $$ Then, by Lagrange multiplier method, the optimal solution is given by $\mu^* (\mathbf{a} \vert \mathbf{s}) = \frac{1}{Z} e^{Q(\mathbf{s},\mathbf{a})}$ where $Z$ is a normalizing factor, yielding the update rule: $$ \hat{Q}^{k + 1} \leftarrow \underset{Q}{\arg \min} \; \alpha \mathbb{E}_{\mathbf{s} \sim \mathcal{D}} \left[ \log \sum_{\mathbf{a} \in \mathcal{A}} e^{Q(\mathbf{s}, \mathbf{a})} - \mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} [Q(\mathbf{s}, \mathbf{a}) ]\right] + \frac{1}{2} \mathbb{E}_{(\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) \sim \mathcal{D}} \left[ \left( Q - \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k \right)^2 \right] $$
2. $\texttt{CQL}(\rho)$
   For an optimization problem of the form that minimizes KL-divergence: $$ \begin{aligned} \max_{\mu} \; \mathbb{E}_{\mathbf{a} \sim \mu (\cdot \vert \mathbf{s})} [Q(\mathbf{s}, \mathbf{a})] + \mathrm{KL} (\mu \Vert \rho) \quad \text{ s.t. }\quad \sum_{\mathbf{a} \in \mathcal{A}} \mu (\mathbf{a} \vert \mathbf{s}) = 1 \end{aligned} $$ Then, by Lagrange multiplier method, the optimal solution is given by $\mu^* (\mathbf{a} \vert \mathbf{s}) = \frac{1}{Z} \rho (\mathbf{a} \vert \mathbf{s}) e^{Q(\mathbf{s},\mathbf{a})}$ where $Z$ is a normalizing factor, yielding the update rule: $$ \hat{Q}^{k + 1} \leftarrow \underset{Q}{\arg \min} \; \alpha \mathbb{E}_{\mathbf{s} \sim \mathcal{D}} \left[ \mathbb{E}_{\mathbf{a} \sim \rho(\cdot \vert \mathbf{s})} \left[ Q(\mathbf{s}, \mathbf{a}) \frac{e^{Q(\mathbf{s}, \mathbf{a})}}{Z} \right] - \mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} [Q(\mathbf{s}, \mathbf{a}) ]\right] + \frac{1}{2} \mathbb{E}_{(\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) \sim \mathcal{D}} \left[ \left( Q - \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k \right)^2 \right] $$

Theoretical analysis

If the mild regularity conditions hold (slow updates on the policy), the following theorem demonstrates that any variants of the CQL learns $\hat{Q}^{k+1}$ of which $\hat{V}^{k + 1}$ lower-bounds the actual value $V^{k+1}$ induced by $Q^{k + 1}$ under the action-distribution defined by $\pi_k$:

$\color{red}{\mathbf{Theorem.}}$ Conservative Q-Learning
Let $\mu^* = \pi_{\hat{Q}_k} \propto \exp \left(\hat{Q}^k (\mathbf{s}, \mathbf{a}) \right)$ and assume that $\mathrm{TV} (\hat{\pi}^{k + 1}, \pi_{\hat{Q}^k}) \leq \varepsilon$ (i.e., $\hat{\pi}^{k + 1}$ changes slowly with respect to $\hat{Q}^k$). Then, the policy value under $\hat{Q}^k$ lower bounds the actual policy value: $$ \hat{V}^{k + 1} (\mathbf{s}) \leq V^{k + 1} (\mathbf{s}) \quad \forall \mathbf{s} \in \mathcal{S} $$ if we can ignore the finite sampling error (e.g., $\alpha$ is sufficiently large, or large dataset $\vert \mathcal{D} \vert \gg 1$) and $$ \mathbb{E}_{\mathbf{a} \sim \pi_{\hat{Q}^k} (\cdot \vert \mathbf{s})} \left[ \frac{\pi_{\hat{Q}^k} (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} - 1 \right] \geq \max_{\begin{gathered} \mathbf{a} \in \mathcal{A} \\ \text{ s.t. } \pi_\beta (\mathbf{a} \vert \mathbf{s}) > 0 \end{gathered}} \left( \frac{\pi_{\hat{Q}^k} (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \right) \cdot \varepsilon $$ The LHS is equal to the amount of conservatism induced in the value $\hat{V}^{k + 1}$ in iteration $k + 1$ of the CQL update if the learned policy were equal to soft-optimal policy for $\hat{Q}^k$, i.e., $\hat{\pi}^{k + 1} = \pi_{\hat{Q}^k}$. And the RHS is the maximal amount of potential overestimation due to the actual difference between the actual policy $\hat{\pi}^{k + 1}$ and $\pi_{\hat{Q}^k}$.

$\mathbf{Proof.}$

In this proof, we compute the difference induced in the policy value $\hat{V}^{k+1}$ derived from the Q-value iterate $\hat{Q}^{k+1}$ with respect to the previous iterate $\hat{\mathcal{B}}^{\pi_k} \hat{Q}^k$. If this difference is negative at each iteration, then the resulting Q-values are guaranteed to lower bound the true policy value as in the proof of the previous theorem.

And we can obtain:

\[\begin{aligned} \mathbb{E}_{\hat{\pi}^{k+1}(\mathbf{a} \vert \mathbf{s})} \left[\hat{Q}^{k+1}(\mathbf{s}, \mathbf{a}) \right] & = \mathbb{E}_{\hat{\pi}^{k+1}(\mathbf{a} \vert \mathbf{s})} \left[ \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right] - \alpha \mathbb{E}_{\hat{\pi}^{k+1}(\mathbf{a} \vert \mathbf{s})} \left[ \frac{\pi_{\hat{Q}^k}(\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} -1 \right] \\ & = \mathbb{E}_{\hat{\pi}^{k+1}(\mathbf{a} \vert \mathbf{s})}\left[ \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right] - \alpha \underbrace{\mathbb{E}_{\pi_{\hat{Q}^k}(\mathbf{a} \vert \mathbf{s})}\left[ \frac{\pi_{\hat{Q}^k}(\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} -1 \right]}_{\text{underestimation, (a)}} \\ &~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ + \alpha \sum_{\begin{gathered} \mathbf{a} \in \mathcal{A} \\ \text{ s.t. } \pi_\beta (\mathbf{a} \vert \mathbf{s}) > 0 \end{gathered}} \underbrace{\left(\pi_{\hat{Q}^k}(\mathbf{a} \vert \mathbf{s}) - \hat{\pi}^{k+1}(\mathbf{a} \vert \mathbf{s}) \right)}_{\text{(b),}~~{\leq \mathrm{TV}(\pi_{\hat{Q}^k}, \hat{\pi}^{k+1})}} \frac{\pi_{\hat{Q}^k}(\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \end{aligned}\]

If $\text{(a)}$ is larger than $\text{(b)}$, then the learned Q-value induces an underestimation in an iteration $k + 1$, and hence, by a recursive argument, the learned Q-value underestimates the optimal Q-value. Note that by upper-bounding $\text{(b)}$ by:

\[\mathrm{TV}(\pi_{\hat{Q}^k}, \hat{\pi}^{k + 1}) \cdot \max_{\begin{gathered} \mathbf{a} \in \mathcal{A} \\ \text{ s.t. } \pi_\beta (\mathbf{a} \vert \mathbf{s}) > 0 \end{gathered}} \frac{\pi_{\hat{Q}^k} (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})}\]

and by the inequalities we assumed, we obtain \(\hat{V}^{k + 1} \leq \mathbb{E}_{\hat{\pi}^{k+1}(\mathbf{a} \vert \mathbf{s})}\left[ \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right]\). Then, by incorporating finite sampling error and regarding $\hat{V}^{k + 1}$ as the fixed point of the $k$-th policy evaluation, which are analogous to the previous theorem, we can show that the inequality of the theorem holds in the case when $\alpha$ is sufficiently large, or $\vert \mathcal{D} \vert \gg 1$.

\[\tag*{$\blacksquare$}\]

Interestingly, the difference in Q-values at in-distribution actions of $\pi_\beta$ and over-optimistically erroneous out-of-distribution actions of $\mu$ is higher than the corresponding difference under the actual Q-function, as proved in the following theorem. The gap expansion suggests that the CQL consistently over-estimate the in-distribution actions than out-of-distribution actions. This yields several advantages:

• CQL backups are expected to be more robust, as the policy is updated using Q-values that prefer in-distribution actions, even when function approximation or sampling error causes out-of-distribution actions to have higher learned Q-values.
• The optimal policy will be constrained to remain closer to $\pi_\beta$, thus the CQL update implicitly discourages out-of-distribution actions.

$\color{red}{\mathbf{Theorem.}}$ CQL is gap-expanding
At any iteration $k$, CQL expands the difference in expected Q-values under the behavior policy $\pi_\beta (\mathbf{a} \vert \mathbf{s})$ and $\mu_k$ (the optimal $\mu$ of $k$-th iteration), such that for large enough values for $\alpha_k$, we have: $$ \forall \mathbf{s} \in \mathcal{S} \; \mathbb{E}_{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \left[ \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mu_k (\mathbf{a} \vert \mathbf{s})} \left[ \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right] > \mathbb{E}_{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \left[ Q^k (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mu_k (\mathbf{a} \vert \mathbf{s})} \left[ Q^k (\mathbf{s}, \mathbf{a}) \right] $$

$\mathbf{Proof.}$

Note that the solution $\hat{Q}^{k + 1}$ of the update rule can be obtained by setting the derivative of the update equation to $0$:

\[\hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) = \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) - \alpha_k \frac{\mu_k (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})}\]

Then, the value of the policy $\mu_k (\mathbf{a} \vert \mathbf{s})$ under $\hat{Q}^{k + 1}$ is given by:

\[\mathbb{E}_{\mathbf{a} \sim \mu_k (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] = \mathbb{E}_{\mathbf{a} \sim \mu_k (\cdot \vert \mathbf{s})} \left[ \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right] - \alpha_k \underbrace{\mu_k^\top \left( \frac{\mu_k (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \right)}_{\hat{\Delta}^k \geq 0}\]

Note that we already prove that $\hat{\Delta}^k \geq 0$ in previous theorems. Also note that the expected amount of extra underestimation introduced at iteration $k$ under action sampled from the behavior policy $\pi_\beta (\mathbf{a} \vert \mathbf{s})$ is $0$:

\[\mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] = \mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} \left[ \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right] - \alpha_k \underbrace{\pi_\beta^\top \left( \frac{\mu_k (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s})}{\pi_\beta (\mathbf{a} \vert \mathbf{s})} \right)}_{0}\]

and thus:

\[\mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mathbf{a} \sim \mu_k (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] = \mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} \left[ \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mathbf{a} \sim \mu_k (\cdot \vert \mathbf{s})} \left[ \hat{\mathcal{B}}^{\pi_k} \hat{Q}^k (\mathbf{s}, \mathbf{a}) \right] - \alpha_k \hat{\Delta}^k\]

By subtracting \(\mathbb{E}_{\pi_\beta (\mathbf{a} \vert \mathbf{s})} [Q^{k + 1} (\mathbf{s}, \mathbf{a})] - \mathbb{E}_{\mu_k (\mathbf{a} \vert \mathbf{s})} [Q^{k + 1} (\mathbf{s}, \mathbf{a})]\):

\[\begin{multline} \mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} [Q^{k + 1} (\mathbf{s}, \mathbf{a})] = \mathbb{E}_{\mathbf{a} \sim \mu_k (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mathbf{a} \sim \mu_k (\cdot \vert \mathbf{s})} [Q^{k + 1} (\mathbf{s}, \mathbf{a})] \\ + \left( \mu_k (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s}) \right)^\top \underbrace{\left[ \hat{\mathcal{B}}^{\pi_k} \left( \hat{Q}^k - Q^k \right) (\mathbf{s}, \cdot)\right]}_{\text{(a)}} - \alpha_k \hat{\Delta}^k \end{multline}\]

By choosing $\alpha_k$ such that any positive bias introduced by the quantity \(( \mu_k (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s}) )^\top \text{(a)}\) is cancelled out:

\[\alpha_k > \max \left( \frac{\left( \mu_k (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s}) \right)^\top \left[ \hat{\mathcal{B}}^{\pi_k} \left( \hat{Q}^k - Q^k \right) (\mathbf{s}, \cdot)\right]}{\hat{\Delta}^k} , 0 \right)\]

we obtain the following gap-expanding relationship:

\[\mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mathbf{a} \sim \pi_\beta (\cdot \vert \mathbf{s})} [Q^{k + 1} (\mathbf{s}, \mathbf{a})] > \mathbb{E}_{\mathbf{a} \sim \mu_k (\cdot \vert \mathbf{s})} \left[ \hat{Q}^{k+1} (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\mathbf{a} \sim \mu_k (\cdot \vert \mathbf{s})} [Q^{k + 1} (\mathbf{s}, \mathbf{a})]\]

Now, to incorporate the finite sampling error, upper-bound the following quantities:

\[\begin{gathered} Q^k \leq \frac{R_{\max}}{1 - \gamma} \\ (\pi_\beta (\mathbf{a} \vert \mathbf{s}) - \mu_k (\mathbf{a} \vert \mathbf{s}))^\top \mathcal{B}^{\pi_k} Q^k (\mathbf{s}, \cdot) \leq \mathrm{TV}(\pi_\beta, \mu_k) \cdot \frac{R_{\max}}{1 - \gamma} \end{gathered}\]

Then, the worst case overestimation due to sampling error is given by \(\frac{C_{\gamma, \mathbb{P}_\mathcal{S}, \delta} R_{\max}}{1 - \gamma}\). In this case, note that with high probability $> 1 - \delta$:

\[\left\vert \hat{\mathcal{B}}^{\pi_k} \left( \hat{Q}^k - Q^k \right) - \mathcal{B}^{\pi_k} \left( \hat{Q}^k - Q^k \right) \right\vert \leq \frac{2 \cdot C_{\gamma, \mathbb{P}_\mathcal{S}, \delta} \cdot R_{\max}}{1 - \gamma}\]

Therefore, the presence of sampling error adds \(\mathrm{TV}(\pi_\beta, \pi_k) \cdot \frac{2 \cdot C_{\gamma, \mathbb{P}_\mathcal{S}, \delta} \cdot R_{\max}}{1 - \gamma}\) to the value of $\alpha_k$. Hence, the sufficient condition on $\alpha_k$ for the gap-expanding property is given by:

\[\alpha_k > \max \left( \frac{\left( \mu_k (\mathbf{a} \vert \mathbf{s}) - \pi_\beta (\mathbf{a} \vert \mathbf{s}) \right)^\top \left[ \mathcal{B}^{\pi_k} \left( \hat{Q}^k - Q^k \right) (\mathbf{s}, \cdot)\right]}{\hat{\Delta}^k} + \mathrm{TV}(\pi_\beta, \pi_k) \cdot \frac{2 \cdot C_{\gamma, \mathbb{P}_\mathcal{S}, \delta} \cdot R_{\max}}{1 - \gamma}, 0 \right)\] \[\tag*{$\blacksquare$}\]

Empirical Results

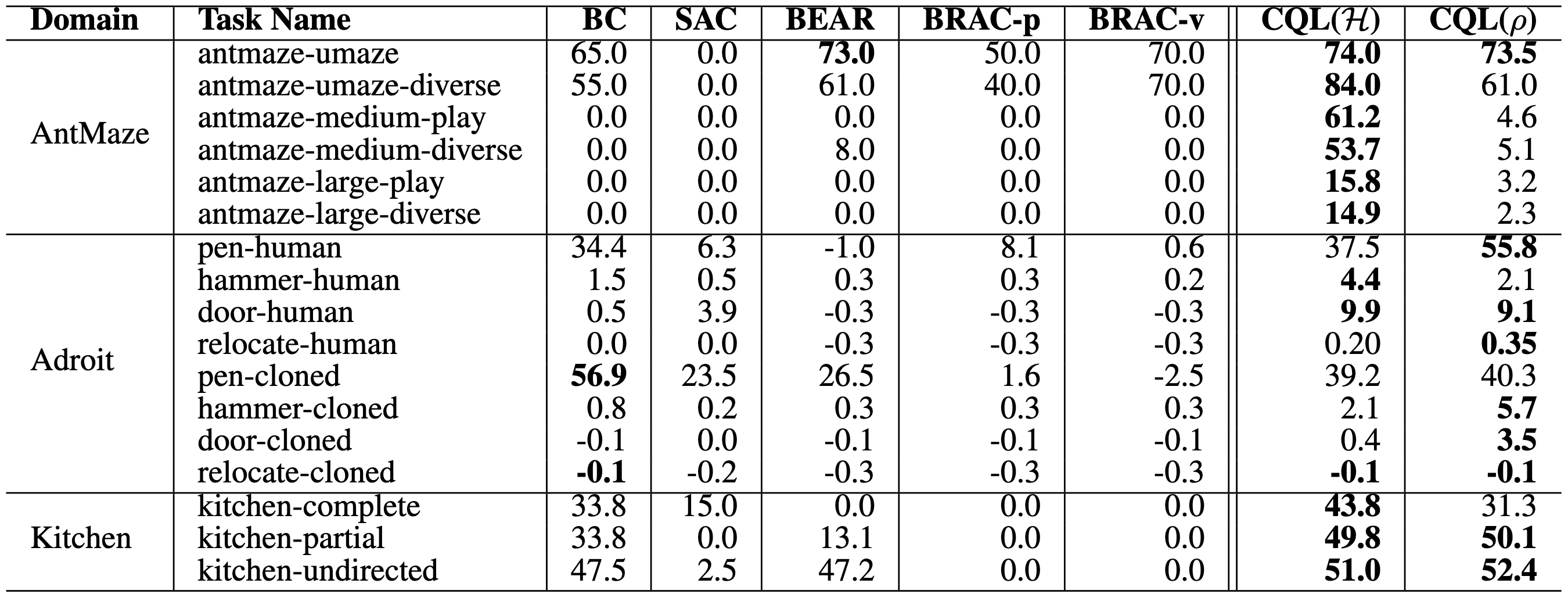
The authors empirically validated that CQL learns lower-bounded Q-values. The following table illustrates the difference between the learned Q-value and the discounted policy return, at intermediate iterations during training. Whereas previous offline RL methods generally overestimate Q-values, CQL effectively learns lower-bounded Q-value estimates.

$\mathbf{Fig\ 4.}$ CQL learns lower-bounded Q-values (Kumar et al., 2020)

Notably, CQL outperforms prior methods on realistic complex datasets, including the AntMaze and Kitchen domains from D4RL. These benchmarks, in particular, necessitate agents to adeptly blend different suboptimal trajectories to achieve success.

$\mathbf{Fig\ 5.}$ Normalized scores on AntMaze, Adroit, and kitchen domains from D4RL (Kumar et al., 2020)

References

[1] Kumar et al., “Conservative Q-Learning for Offline Reinforcement Learning”, NeurIPS 2020
[2] Aviral Kumar and Avi Singh, “Offline Reinforcement Learning: How Conservative Algorithms Can Enable New Applications”