[RL] Offline-Boosted Actor-Critic (OBAC)
The reliance on extensive environment interaction hampers the real-world deployment of online off-policy RL. Alternatives such as model-based RL and offline RL are proposed, but they still face issues like computational complexity and distributional shift. The paper Luo et al. explores using offline optimal policy to enhance the efficiency and performance of online off-policy RL.
As a result, they propose a model-free online RL framework, Offline-Boosted Actor-Critic (OBAC), which identifies superior offline policies through value comparison and uses them as adaptive constraints to ensure stronger policy learning performance.
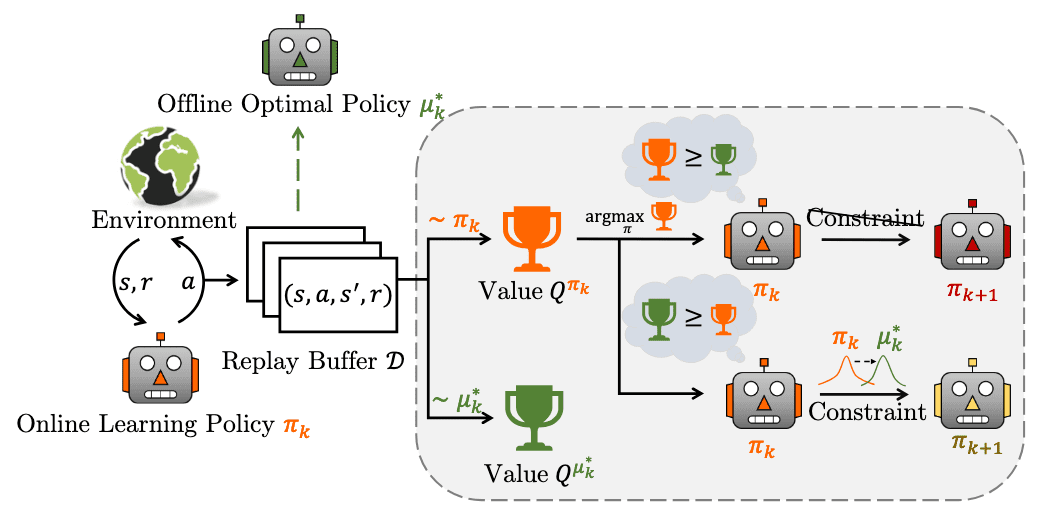
Offline-Boosted Off-Policy Iteration
At the $k$-th iteration step, denote the online learning policy as $\pi_k$. Concurrently, the replay buffer $\mathcal{D}$ allows us to derive a concurrent offline optimal policy $\mu_k^*$:
\[\mu_k^* = \arg \max \; \mathbb{E}_{\mathbf{a} \sim \mathcal{D}} \left[ Q^{\mu_k} (\mathbf{s}, \mathbf{a}) \right]\]Considering the offline optimal policy \(\mu_k^*\) as a guidance policy to assist in generating a new online learning policy $\pi_{k + 1}$, the occurrence of the superiority of \(\mu_k^*\) varies across tasks as well as different training stages. Consequently, the authors designed the following adaptive mechanism:
- $V^{\pi_k} (\mathbf{s}) \geq V^{\mu_k^*} (\mathbf{s})$
This implies that even using the optimal actions in the replay buffer $\mathcal{D}$, the online learning policy $\pi_k$ would still outperform them. We can directly solve the objective function without introducing $\mu_k^*$, thereby avoiding potential negative effects. - $V^{\pi_k} (\mathbf{s}) \leq V^{\mu_k^*} (\mathbf{s})$
In this case, we can identify superior actions in the replay buffer $\mathcal{D}$ compared to the current learning policy. Hence, we may add a policy constraint into the objective function to integrate the distribution of better actions from the offline optimal policy as a guidance.
Formally, offline-boosted policy iteration improves $\pi_k$ as follows:
\[\begin{gathered} \pi_{k + 1} = \underset{\pi}{\arg \max} \; \mathbb{E}_{\mathbf{a} \sim \pi} \left[ Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right] \\ \text{ s.t. } \int_{\mathbf{a} \in \mathcal{A}} f \left( \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\mu_k^* (\mathbf{a} \vert \mathbf{s})} \right) \delta \left( V^{\mu_k^*} (\mathbf{s}) \geq V^{\pi_k} (\mathbf{s}) \right) \mu_k^* (\mathbf{a} \vert \mathbf{s}) \; \mathrm{d} \mathbf{a} \leq \varepsilon \end{gathered}\]where $f (\cdot)$ is a regularization function and $\delta$ is a Dirac-delta function.
If $V^{\mu_k^*} (\mathbf{s}) \geq V^{\pi_k} (\mathbf{s})$, the closed-form solution of $\pi_{k+1}$ is given by: $$ \pi_{k+1} (\mathbf{a} \vert \mathbf{s}) = \frac{1}{Z (\mathbf{s})} \mu_k^* (\mathbf{a} \vert \mathbf{s}) (f^\prime)^{-1} \left( Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right) $$ where $Z (\mathbf{s})$ is the normalization factor of action distribution. When $V^{\mu_k^*} (\mathbf{s}) \geq V^{\pi_k} (\mathbf{s})$, $\pi_{k+1}$ is an ordinary solution to maximize $Q^{\pi_k} (\mathbf{s}, \mathbf{a})$.
$\mathbf{Proof.}$
Introducing Lagrange multiplier $\lambda_1$ and $\lambda_2$, we have the following optimization loss:
\[\begin{multline} \mathcal{L} (\pi, \lambda_1, \lambda_2) = \mathbb{E}_{\mathbf{a} \sim \pi} \left[ Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right] \\ + \lambda_1 \left( \varepsilon - \int_{\mathbf{a} \in \mathcal{A}} f \left( \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\mu_k^* (\mathbf{a} \vert \mathbf{s})} \right) \delta \left( V^{\mu_k^*} (\mathbf{s}) \geq V^{\pi_k} (\mathbf{s}) \right) \mu_k^* (\mathbf{a} \vert \mathbf{s}) \mathrm{d} \mathbf{a} \right) \\ + \lambda_2 \left( 1 - \int_{\mathbf{a} \in \mathcal{A}} \pi (\mathbf{a} \vert \mathbf{s}) \mathrm{d} \mathbf{a} \right) \end{multline}\]By differentiating with respect to $\pi$:
\[\begin{aligned} \frac{\partial \mathcal{L}}{\partial \pi} & = Q^{\pi_k} (\mathbf{s}, \mathbf{a}) - \lambda_1 \mu_k^* (\mathbf{a} \vert \mathbf{s}) \frac{\delta \left( V^{\mu_k^*} (\mathbf{s}) \geq V^{\pi_k} (\mathbf{s}) \right)}{\mu_k^* (\mathbf{a} \vert \mathbf{s})} f^\prime \left( \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\mu_k^* (\mathbf{a} \vert \mathbf{s})} \right) - \lambda_2 \\ & = Q^{\pi_k} (\mathbf{s}, \mathbf{a}) - \lambda_1 \delta \left( V^{\mu_k^*} (\mathbf{s}) \geq V^{\pi_k} (\mathbf{s}) \right) f^\prime \left( \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\mu_k^* (\mathbf{a} \vert \mathbf{s})} \right) - \lambda_2 \end{aligned}\]Setting $\frac{\partial \mathcal{L}}{\partial \pi} = 0$ and considering \(V^{\mu_k^*} (\mathbf{s}) \geq V^{\pi_k} (\mathbf{s})\), we have:
\[\pi_{k + 1} \propto \mu_k^* (\mathbf{a} \vert \mathbf{s}) (f^\prime)^{-1} \left( Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right)\]In contrast, if \(V^{\mu_k^*} (\mathbf{s}) < V^{\pi_k} (\mathbf{s})\), we do not introduce the constraint to the optimization. Thus, $\pi_{k+1}$ will be an ordinary solution to maximize $Q^{\pi_k} (\mathbf{s}, \mathbf{a})$.
\[\tag*{$\blacksquare$}\]The following theorem shows that $\pi_{k+1}$ would have a higher value than $\pi_k$ w.r.t. the state-action distribution of the replay buffer.
For all $(\mathbf{s}, \mathbf{a}) \in \mathcal{D}$: $$ Q^{\pi_{k+1}} (\mathbf{s}, \mathbf{a}) \geq Q^{\pi_k} (\mathbf{s}, \mathbf{a}) $$ with the offline optimal policy $\mu_k^*$ serving as a performance baseline policy.
$\mathbf{Proof.}$
If \(V^{\mu_k^*} (\mathbf{s}) < V^{\pi_k} (\mathbf{s})\), we do not introduce the constraint to the optimization. Thus, $\pi_{k+1}$ will be an ordinary solution to maximize $Q^{\pi_k} (\mathbf{s}, \mathbf{a})$. Thus, we can only consider the case \(V^{\mu_k^*} (\mathbf{s}) \geq V^{\pi_k} (\mathbf{s})\).
Then, by definition of $\mu_k^*$ and the inequality:
\[\int_{\mathbf{a} \in \mathcal{A}} \frac{1}{Z(\mathbf{s})} (f^\prime)^{-1} \left( Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right) \geq \int_{\mathbf{a} \in \mathcal{A}} \frac{1}{Z(\mathbf{s})} \mu_k^* (\mathbf{a} \vert \mathbf{s}) (f^\prime)^{-1} \left( Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right) = 1\]we have:
\[\begin{aligned} \mathbb{E}_{\mathbf{a} \sim \pi_{k+1}} \left[ Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right] & = \int_{\mathbf{a} \sim \mathcal{A}} \pi_{k+1} (\mathbf{a} \vert \mathbf{s}) Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \mathrm{d} \mathbf{a} \\ & = \int_{\mathbf{a} \sim \mathcal{A}} \frac{1}{Z (\mathbf{s})} \mu_k^* (\mathbf{a} \vert \mathbf{s}) (f^\prime)^{-1} \left( Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right) Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \mathrm{d} \mathbf{a} \\ & = \int_{\mathbf{a} \sim \mathcal{A}} \frac{1}{Z (\mathbf{s})} \left[ \underset{\mathbf{a} \sim \mathcal{D}}{\arg \max} \; Q^{\color{red}{\mu_k^*}} (\mathbf{s}, \mathbf{a}) \right] (f^\prime)^{-1} \left( Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right) Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \mathrm{d} \mathbf{a} \\ & \geq \int_{\mathbf{a} \sim \mathcal{A}} \frac{1}{Z (\mathbf{s})} \left[ \underset{\mathbf{a} \sim \mathcal{D}}{\arg \max} \; Q^{\color{red}{\pi_k}} (\mathbf{s}, \mathbf{a}) \right] (f^\prime)^{-1} \left( Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right) Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \mathrm{d} \mathbf{a} \\ & \geq \int_{\mathbf{a} \sim \mathcal{A}} \color{blue}{\frac{1}{Z (\mathbf{s})}} \pi_k (\mathbf{a} \vert \mathbf{s}) \color{blue}{(f^\prime)^{-1} \left( Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right)} Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \mathrm{d} \mathbf{a} \\ & \geq \int_{\mathbf{a} \sim \mathcal{A}} \pi_k (\mathbf{a}\vert \mathbf{a}) Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \mathrm{d} \mathbf{a} \\ & = \mathbb{E}_{\mathbf{a} \sim \pi_k} \left[Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right] \end{aligned}\]Therefore, \(\mathbb{E}_{\mathbf{a} \sim \pi_k} \left[Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right] \leq \mathbb{E}_{\mathbf{a} \sim \pi_{k+1}} \left[ Q^{\pi_k} (\mathbf{s}, \mathbf{a}) \right]\). Finally, we come to the following inequality:
\[\begin{aligned} Q^{\pi_k} (\mathbf{s}_t, \mathbf{a}_t) & = r(\mathbf{s}_t, \mathbf{a}_t) + \gamma \mathbb{E}_{\mathbf{s}_{t+1}, \mathbf{a}_{t+1} \sim \pi_k} \left[ Q^{\pi_k} (\mathbf{s}_{t + 1}, \mathbf{a}_{t + 1}) \right] \\ & \leq r(\mathbf{s}_t, \mathbf{a}_t) + \gamma \mathbb{E}_{\mathbf{s}_{t+1}, \mathbf{a}_{t+1} \sim \pi_{k + 1}} \left[ Q^{\pi_k} (\mathbf{s}_{t + 1}, \mathbf{a}_{t + 1}) \right] \\ & \quad \vdots \\ & = Q^{\pi_{k + 1}} (\mathbf{s}_t, \mathbf{a}_t) \end{aligned}\] \[\tag*{$\blacksquare$}\]With the convergence of policy evaluations on $\pi_k$ and $\mu_k^*$, alongside the outcomes of policy improvement, we can alternate between these steps. Consequently, the online learning policy will demonstrably converge to the optimal policy \(\pi^*\):
Assuming a finite action space $\vert \mathcal{A} \vert < \infty$, repeating the alternation of the naïve policy evaluations on $\pi_k$ and $\mu_k^*$ and offline-boosted policy improvement that yields $\pi_{k + 1}$, can make any online learning policy $\pi_k \in \Pi$ converge to the optimal policy $\pi^*$ such that: $$ \forall (\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}: \; Q^{\pi^*} (\mathbf{s}, \mathbf{a}) \geq Q^{\pi_k} (\mathbf{s}, \mathbf{a}) $$
$\mathbf{Proof.}$
At each iteration, we guarantee the sequence \(\{ Q^{\pi_k} \}_{k=1}\) is monotonically increasing. Furthermore, for all state-action pairs, $Q^{\pi_k}$ would converge by repeatedly using the Bellman expecation operator as a $\gamma$-contraction mapping.
Thus, the sequence of $\pi_k$ converges to some \(\pi^*\) that are local optimum. To show the global optimality of \(\pi^*\), let any policy \(\pi^\prime \in \Pi\) be given. Note that \(\pi^* = \underset{\pi \in \Pi}{\arg \max} \; \mathbb{E}_{\mathbf{a} \sim \pi} [Q^{\pi^*} (\mathbf{s}, \mathbf{a})]\). That is:
\[\mathbb{E}_{\mathbf{a} \sim \pi^*} [Q^{\pi^*} (\mathbf{s}, \mathbf{a})] \geq \mathbb{E}_{\mathbf{a} \sim \pi^\prime} [Q^{\pi^*} (\mathbf{s}, \mathbf{a})]\]Again, we obtain the following inequality for all $(\mathbf{s}_t, \mathbf{a}_t) \in \mathcal{S} \times \mathcal{A}$:
\[\begin{aligned} Q^{\pi^*} (\mathbf{s}_t, \mathbf{a}_t) & = r(\mathbf{s}_t, \mathbf{a}_t) + \gamma \mathbb{E}_{\mathbf{s}_{t+1}, \mathbf{a}_{t+1} \sim \pi^*} \left[ Q^{\pi^*} (\mathbf{s}_{t + 1}, \mathbf{a}_{t + 1}) \right] \\ & \geq r(\mathbf{s}_t, \mathbf{a}_t) + \gamma \mathbb{E}_{\mathbf{s}_{t+1}, \mathbf{a}_{t+1} \sim \pi^\prime} \left[ Q^{\pi^*} (\mathbf{s}_{t + 1}, \mathbf{a}_{t + 1}) \right] \\ & \quad \vdots \\ & = Q^{\pi^\prime} (\mathbf{s}_t, \mathbf{a}_t) \end{aligned}\] \[\tag*{$\blacksquare$}\]Offline-Boosted Actor-Critic
Offline-Boosted Actor Critic (OBAC) is an actor-critic modification of offline-boosted policy iteration. It maintains two critics $Q_\phi^\pi$ and \(Q_\phi^{\mu^*}\) (and its induced state-value \(V_\psi^{\mu^*}\)) and one actor $\pi_\theta$, which are updated as follows:
Critic Update
First, the online critic $Q_\phi^\pi$ is updated by Bellman expectation equation:
\[\mathcal{L}^\pi (\phi) = \mathbb{E}_{(\mathbf{s}, \mathbf{a}, r, \mathbf{s}^\prime) \sim \mathcal{D}} \left[ \frac{1}{2} \left( r + \gamma \mathbb{E}_{\mathbf{a}^\prime \sim \pi (\cdot \vert \mathbf{s}^\prime)} \left[ Q_\phi^\pi (\mathbf{s}^\prime, \mathbf{a}^\prime) \right] Q_\phi^\pi (\mathbf{s}, \mathbf{a}) \right)^2 \right]\]and its induced state-value function is evaluated as:
\[V^\pi (\mathbf{s}) = \mathbb{E}_{\mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} \left[ Q_\phi^\pi (\mathbf{s}, \mathbf{a}) \right]\]To remove the necessity of $\arg \max_{\mathbf{a}^\prime \sim \mathcal{D}}$ operator of the offline optimal policy \(\mu^*\), the authors employed expectile regression of the implicit Q-learning (IQL) to achieve \(V_\psi^{\mu^*} (\mathbf{s})\):
\[\mathcal{L}^{\mu^*} (\psi) = \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim \mathcal{D}} \left[ \mathcal{L}_2^\tau \left( Q_\phi^{\mu^*} (\mathbf{s}, \mathbf{a}) - V_\psi^{\mu^*} (\mathbf{s}) \right) \right]\]and \(Q_\phi^{\mu^*} (\mathbf{s}, \mathbf{a})\):
\[\mathcal{L}^{\mu^*} (\phi) = \mathbb{E}_{(\mathbf{s}, \mathbf{a}, r, \mathbf{s}^\prime) \sim \mathcal{D}} \left[ \frac{1}{2} \left( r + \gamma V_\psi^{\mu^*} (\mathbf{s}^\prime) - Q_\phi^{\mu^*} (\mathbf{s}, \mathbf{a}) \right)^2 \right]\]where \(\mathcal{L}_2^\tau (u) = \vert \tau - \mathbf{1}(u < 0) \vert u^2\). In the IQL paper, it is theoretically proved that when $\tau \to 1$, the term \(\max_{\mathbf{a}^\prime \sim \mathcal{D}} Q_\phi^{\mu^*} (\mathbf{s}^\prime, \mathbf{a}^\prime)\) can be replaced by \(V_\psi^{\mu^*} (\mathbf{s}^\prime)\):
\[\lim_{\tau \to 1} V_\psi^{\mu^*} (\mathbf{s}) = \max_{\begin{gathered} \mathbf{a} \in \mathcal{A} \\ \text{ s.t. } \pi_\beta (\mathbf{a} \vert \mathbf{s}) > 0 \end{gathered}} Q_\phi^{\mu^*} (\mathbf{s}^\prime, \mathbf{a}^\prime)\]Actor Update
Due to intractability of the closed-form solution, OBAC instead approximate $\pi_{k+1}$ by choosing $f(x) = x \log x$:
\[\pi_{k+1} \approx \underset{\pi \in \Pi}{\arg \min} \; \begin{cases} \mathrm{KL} \left(\pi \middle\Vert \dfrac{\exp \left(Q^{\pi_k} \right)}{Z} \right) & V^{\pi_k} \geq V^{\mu_k^*} \\ \mathrm{KL} \left(\pi \middle\Vert \dfrac{\mu_k^* \exp \left(Q^{\pi_k} \right)}{Z} \right) & V^{\pi_k} \leq V^{\mu_k^*} \\ \end{cases}\]Since $\mu_k^*$ is not available, it is further approximated with behavior cloning constraints, yielding:
\[\begin{aligned} \mathcal{L}(\theta) = & \mathbb{E}_{\mathbf{s} \sim \mathcal{D}} \Big[ \mathbb{E}_{\mathbf{a} \sim \pi_\theta}[\log\pi_\theta(\mathbf{a} \vert \mathbf{s})-Q^{\pi_k}(\mathbf{s}, \mathbf{a})] \\ &\quad -\lambda \cdot \mathbb{E}_{\mathbf{a} \sim \mathcal{D}}[\log\pi_\theta(\mathbf{a} \vert \mathbf{s})] \cdot \delta \left(V^{\mu^*_k}(\mathbf{s})\geq V^{\pi_k}(\mathbf{s})\right) \Big] \end{aligned}\]

Experimental Results
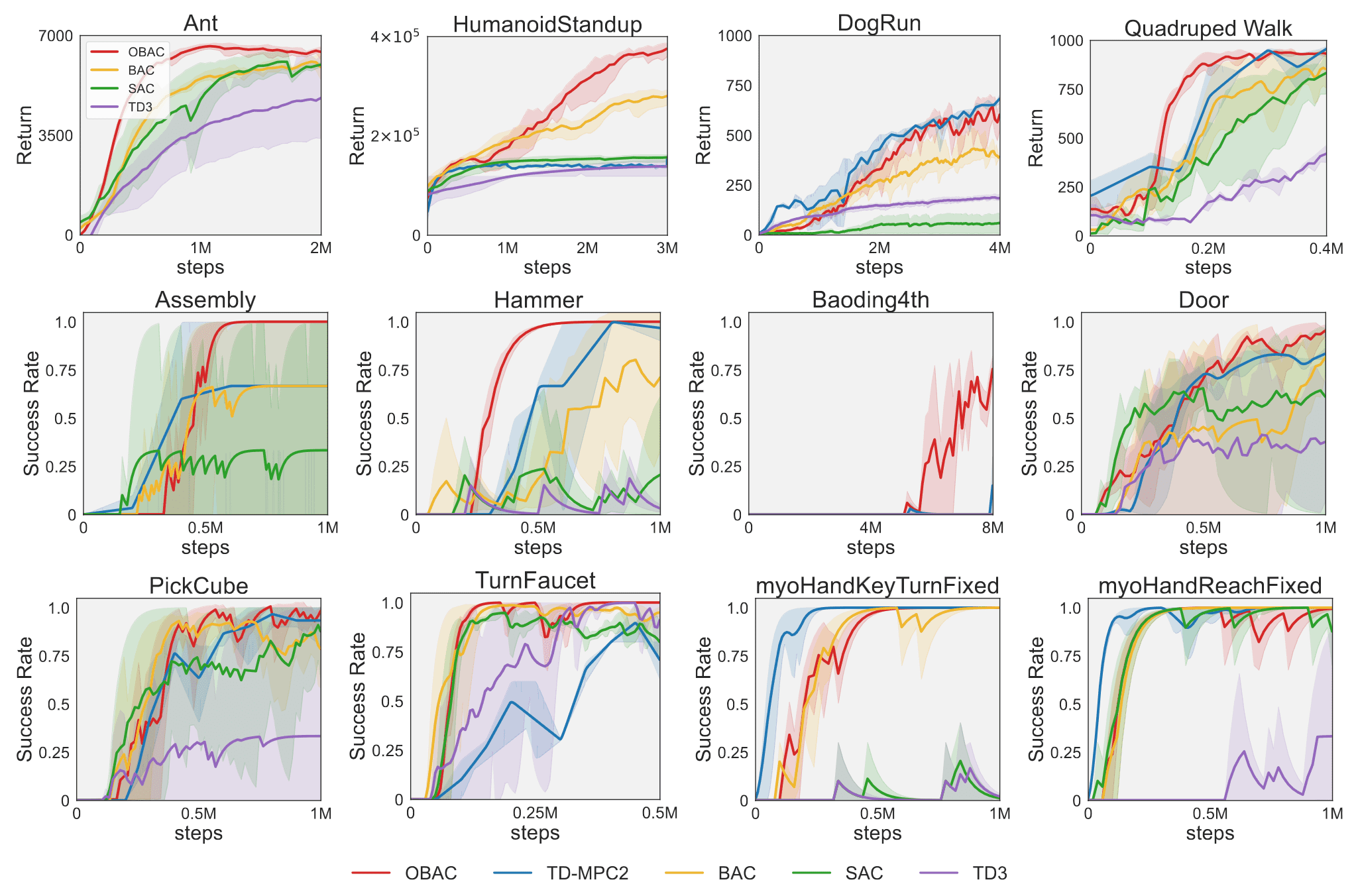
As a result, OBAC, as a model-free RL method, obviously surpasses other model-free RL baselines and demonstrates comparable capabilities to model-based RL methods in terms of exploration efficiency and asymptotic performance.
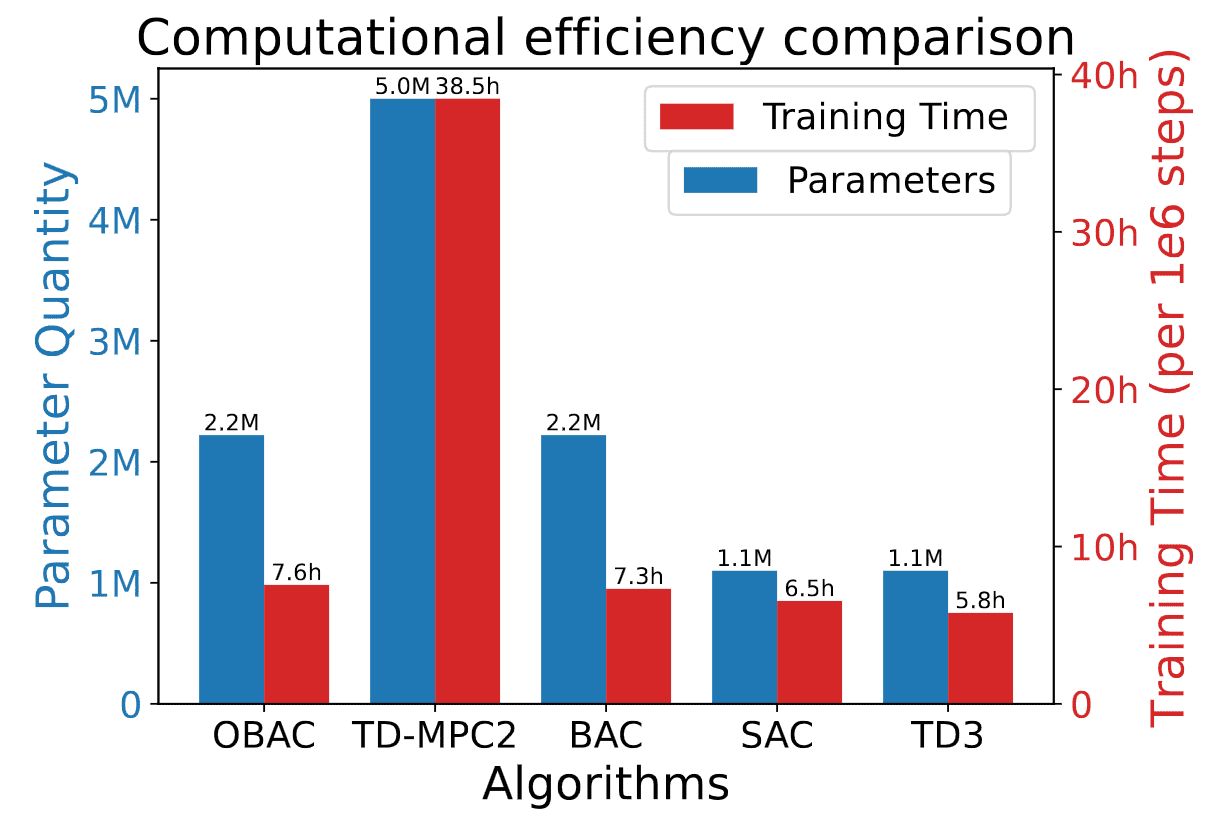
Furthermore, although OBAC involves the training of the offline policy $\mu^*$, OBAC could achieve a similar level of simplicity as other model-free RL methods, requiring only 50% of the parameters and 20% of the training time compared to model-based RL methods.
References
[1] Luo et al., “Offline-Boosted Actor-Critic: Adaptively Blending Optimal Historical Behaviors in Deep Off-Policy RL”, ICML 2024 Poster
[2] Kostrikov et al., “Offline Reinforcement Learning with Implicit Q-Learning”, ICLR 2022 Poster

Leave a comment