[RL] Adversarial Inverse RL
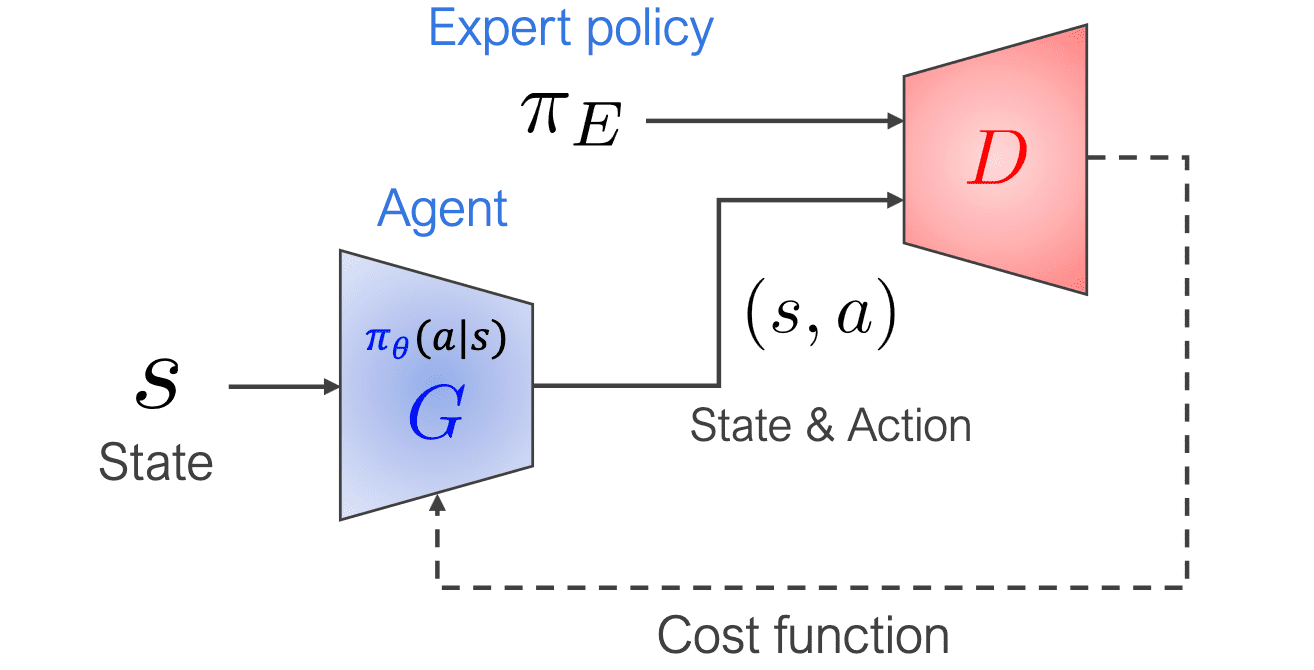
Generative adversarial networks (GANs) are a category of generative models wherein a generator $G$ is trained to optimize a cost function simultaneously learned by a discriminator $D$. In the field of RL, Finn et al. 2016 showed that Max-Ent IRL methods are, in fact, mathematically equivalent to GANs; however, unlike GANs that is an implicit generative models, the generator’s density can be explicitly evaluated and provided as an additional input to the discriminator. In this post, we will explore this equivalence in detail, discussing the theoretical underpinnings.
Preliminaries
Generative Adversarial Network (GAN)
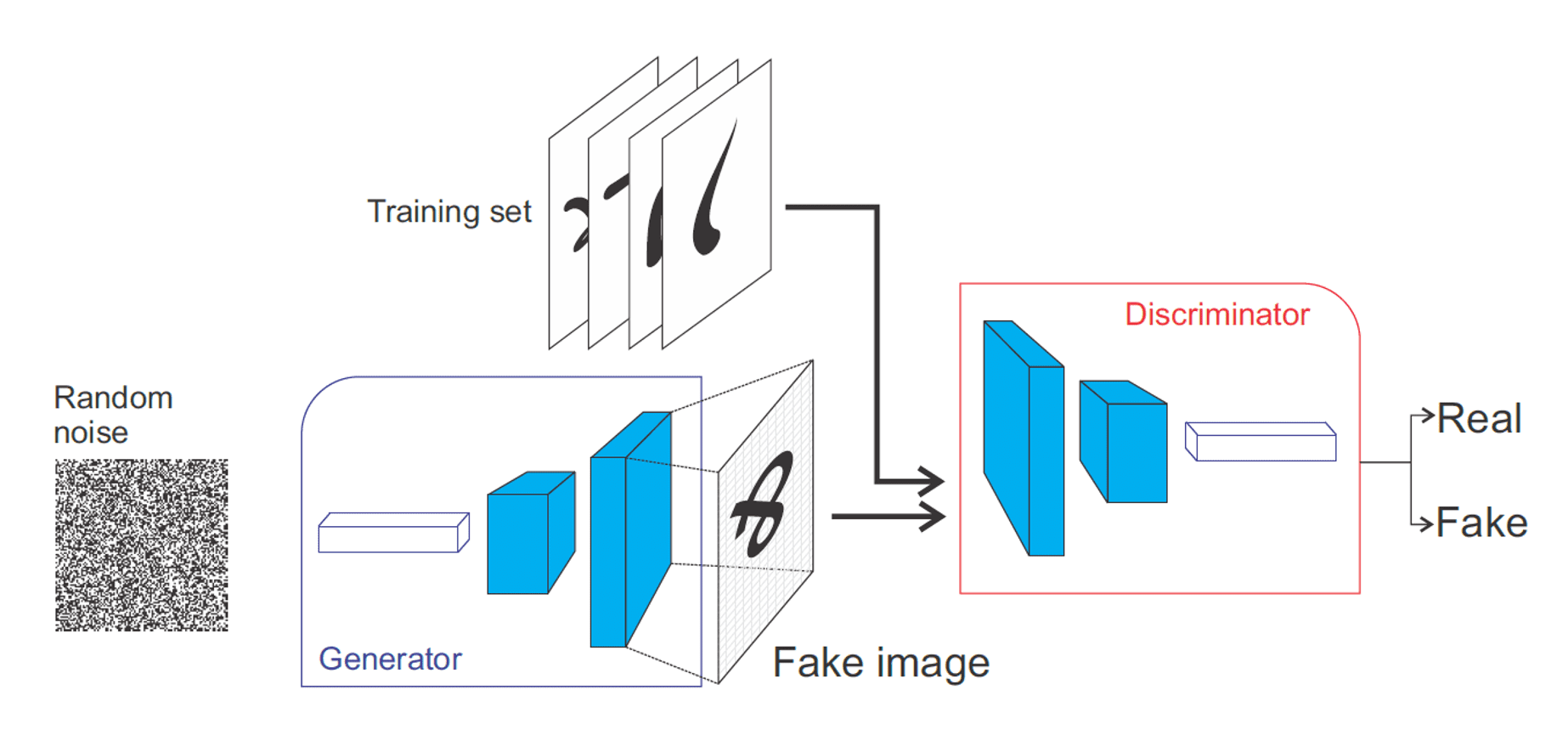
Generative adversarial network (GAN) generates a sample $\mathbf{x} \in \mathcal{X}$ from the latent vector $\mathbf{z}$ with a generator $\mathbf{G} (\mathbf{z}) = \mathbf{x}$. To train $G$, it alternates between learning a discriminator $D: \mathcal{X} \to [0, 1]$ to distinguish between the generated sample and real data
\[D^* = \underset{D}{\arg \min} \; \left\{ \mathcal{L}_D = - \mathbb{E}_{\mathbf{z} \sim p_\mathbf{z}} \left[ \log ( 1 - D (G(\mathbf{z})) ) \right] - \mathbb{E}_{\mathbf{x} \sim p_{\texttt{data}}} \left[ \log D (\mathbf{x} ) \right] \right\}\]and training the generator $G (\mathbf{z})$ to produce samples that appear “real” to $D (\mathbf{x})$ by maximizing $\mathcal{L}_D$, i.e., $G^* = \arg \max_G \min_D \mathcal{L}_D$. Note that the optimal discriminator $D^*$ satisfies:
\[D^* (\mathbf{x}) = \frac{p_{\texttt{data}} (\mathbf{x})}{p_{\texttt{data}} (\mathbf{x}) + p_g (\mathbf{x})}\]where $p_g$ is the density of samples generated by $G$. By plugging it into the objective, we can prove that the GAN optimization problem of the generator $G$ equals to the minimization of Jensen-Shannon divergence (JSD):
\[\begin{aligned} \mathcal{L}_{D^*} & = - \mathbb{E}_{\mathbf{z} \sim p_\mathbf{z}} \left[ \log ( 1 - D^* (G(\mathbf{z})) ) \right] - \mathbb{E}_{\mathbf{x} \sim p_{\texttt{data}}} \left[ \log D^* (\mathbf{x}) \right] \\ & = - \mathbb{E}_{\mathbf{x} \sim p_g} \left[ \log \frac{p_g (\mathbf{x})}{p_{\texttt{data}} (\mathbf{x}) + p_g (\mathbf{x})} \right] - \mathbb{E}_{\mathbf{x} \sim p_{\texttt{data}}} \left[ \log \frac{p_{\texttt{data}} (\mathbf{x})}{p_{\texttt{data}} (\mathbf{x}) + p_g (\mathbf{x})} \right] \\ & = - \mathbb{E}_{\mathbf{x} \sim p_g} \left[ \log \frac{p_g (\mathbf{x})}{\frac{p_{\texttt{data}} (\mathbf{x}) + p_g (\mathbf{x})}{2}} \right] - \mathbb{E}_{\mathbf{x} \sim p_{\texttt{data}}} \left[ \log \frac{p_{\texttt{data}} (\mathbf{x})}{\frac{p_{\texttt{data}} (\mathbf{x}) + p_g (\mathbf{x})}{2}} \right] + \log 4 \\ & = - \mathrm{KL} \left( p_g \Vert \frac{p_{\texttt{data}} + p_g}{2} \right) - \mathrm{KL} \left( p_{\texttt{data}} \Vert \frac{p_{\texttt{data}} + p_g}{2} \right) + \log 4 \\ & = - 2 \cdot \mathrm{JSD}(p_\texttt{data}, p_g) + \log 4 \end{aligned}\]Therefore, the generator $G$ is optimal if and only if $p_g = p_\texttt{data}$. However, in practice, such mini-max criteria of GAN can suffer from the vanishing gradients for generator $G$ at the beginning of training as generator performs very bad and discriminator can easily tell apart real and fake. This leads to $D (G (\mathbf{z})) \approx 0$ that makes the gradient of $\log (1 - D (G (\mathbf{z})))$ to be vanished. Therefore, we instead optimize the alternative non-saturating loss $- \log D (G (\mathbf{z}))$ for the generator:
\[\mathcal{L}_G = \mathbb{E}_{\mathbf{z} \sim p_\mathbf{z}} \left[ - \log D (G (\mathbf{z})) \right]\]
Maximum Entropy (Max-Ent) IRL
Maximum Entropy (Max-Ent) IRL eliminates the presence of degenerate and multiple solutions in the IRL problem by trying to make the estimated distribution of expert’s trajectory $p (\tau \vert r_\boldsymbol{\theta})$ as being no more committed to any particular path as possible. This is achieved by maximizing the Shannon entropy, which is equivalent to maximizing the likelihood due to primal-dual relationship when $p (\tau)$ is modeled as an energy-based model:
\[\mathcal{L}_{\texttt{reward}} (\boldsymbol{\theta}) = \mathbb{E}_{\tau \sim \mathcal{D}} \left[ \log p_\boldsymbol{\theta} (\tau) \right] = \mathbb{E}_{\tau \sim p} \left[ r_\boldsymbol{\theta} (\tau) \right] - \log Z (\boldsymbol{\theta}) \text{ where } p_\boldsymbol{\theta} (\tau) = \frac{1}{Z (\boldsymbol{\theta})} \exp \left( r_\boldsymbol{\theta} (\tau) \right)\]Here, $r_\boldsymbol{\theta} (\tau) = \sum_{(\mathbf{s}, \mathbf{a}) \in \tau} r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a})$ is an accumulated reward throughout the trajectory $\tau$ and $Z (\boldsymbol{\theta})$ is the partition function. For the proof of dual relationship, please refer to my previous post.
To optimize, consider the gradient of the loss under the dataset \(\mathcal{D} = \{ \tau_i \}_{i=1}^N\) of $N$ trajectories:
\[\begin{aligned} \nabla_{\boldsymbol{\theta}} \mathcal{L}_{\texttt{reward}} (\boldsymbol{\theta}) & = \nabla_{\boldsymbol{\theta}} \frac{1}{N} \sum_{i=1}^N \log p_\boldsymbol{\theta} (\tau_i) = \nabla_{\boldsymbol{\theta}} \left[ \frac{1}{N} \sum_{i=1}^N r_\boldsymbol{\theta} (\tau_i) - \log Z (\boldsymbol{\theta}) \right] \\ & = \frac{1}{N} \sum_{i=1}^N \nabla_{\boldsymbol{\theta}} r_\boldsymbol{\theta} (\tau_i) - \frac{1}{Z (\boldsymbol{\theta})} \int \nabla_{\boldsymbol{\theta}} \exp (r_\boldsymbol{\theta} (\tau)) d \tau \\ & = \frac{1}{N} \sum_{i=1}^N \nabla_{\boldsymbol{\theta}} r_\boldsymbol{\theta} (\tau_i) - \int \nabla_{\boldsymbol{\theta}} r_\boldsymbol{\theta} (\tau) p_\boldsymbol{\theta} (\tau) d \tau \\ & = \frac{1}{N} \sum_{i=1}^N \nabla_{\boldsymbol{\theta}} r_\boldsymbol{\theta} (\tau_i) - \mathbb{E}_{\tau \sim p_\boldsymbol{\theta}} \left[ \nabla_{\boldsymbol{\theta}} r_\boldsymbol{\theta} (\tau) \right] \\ \end{aligned}\]where the second term can be estimated through Monte Carlo sampling.
Guided Cost Learning (GCL)
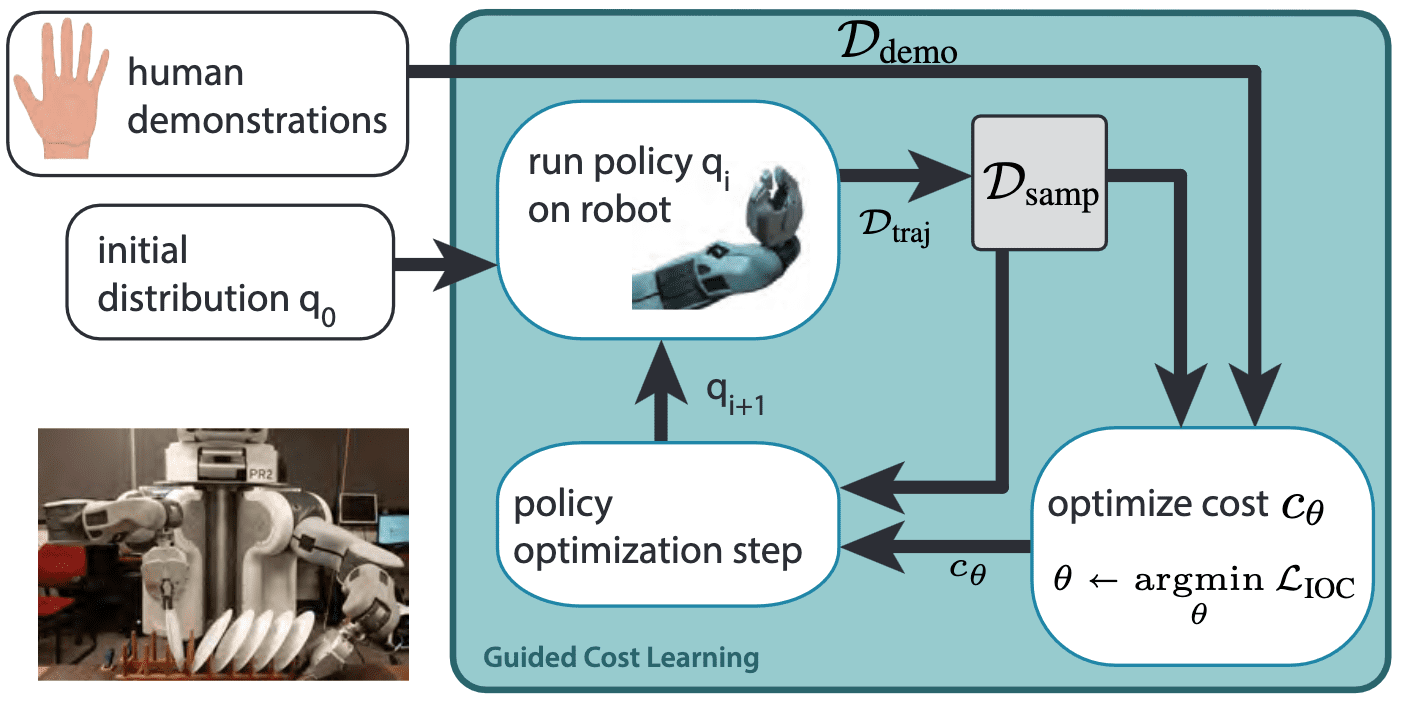
Approximating the gradient of maximum entropy IRL is computationally expensive, as it requires estimating the partition function $Z (\boldsymbol{\theta})$ for $p_\boldsymbol{\theta} (\tau)$ and repeating this process with each update of the reward parameters $\boldsymbol{\theta}$. Guided cost learning, proposed by Finn et al. ICML 2016, introduces an efficient sample-based method for gradient approximation using importance sampling. This approach has proven effective in robotics applications, scaling to high-dimensional state and action spaces and accommodating non-linear cost (reward) functions.
Importance sampling for partition function $Z (\boldsymbol{\theta})$
Suppose we have the distribution $p$ that is intractable to sample from due to the normalization factor $Z$, butwe can evaluate an unnormalized density $\tilde{p} (x) = Z \cdot p (x)$. In this scenario, for a given function $f: \mathcal{X} \to \mathbb{R}$ in which we are interested and another distribution $q (X)$ that is easy to compute, we can rewrite the expectation $\mathbb{E}_{x \sim p} \left[ f (x) \right]$ using importance sampling as follows:
\[\mathbb{E}_{x \sim p} \left[ f (x) \right] = \int f (x) \frac{p(x)}{q(x)} q(x) dx = \frac{1}{Z} \int f(x) \frac{\tilde{p}(x)}{q(x)} q(x) dx = \frac{1}{\alpha} \mathbb{E}_{x \sim q} \left[ \frac{\tilde{p}(x)}{q(x)} f(x) \right]\]Furthermore, we can evaluate $Z$ using an expectation with respect to $q$:
\[\alpha = \alpha \int p (x) dx = \int \tilde{p}(x) dx = \int \frac{\tilde{p}(x)}{q(x)} q(x) dx = \mathbb{E}_{x \sim q} \left[ \frac{\tilde{p}(x)}{q(x)} \right]\]This leads to the importance weight $w(x) = \tilde{p} (x) / q(x)$, removing the need to sample from $p$ or evaluate its density:
\[\mathbb{E}_{x \sim p} \left[ f(x) \right] = \mathbb{E}_{x \sim q} \left[ \frac{w(x)}{\mathbb{E}_{x^\prime \sim q} \left[ w (x^\prime) \right]} f(x) \right]\]Analogously, we can integrate this discussion into the Max-Ent IRL formulation to avoid computing intractable $Z (\boldsymbol{\theta})$:
\[\nabla_{\boldsymbol{\theta}} \mathcal{L}_{\texttt{reward}} (\boldsymbol{\theta}) = \frac{1}{N} \sum_{i=1}^N \nabla_{\boldsymbol{\theta}} r_\boldsymbol{\theta} (\tau_i) - \mathbb{E}_{\tau \sim q} \left[ \frac{w_\boldsymbol{\theta} (\tau^\prime)}{\mathbb{E}_{\tau^\prime \sim q} \left[ w_\boldsymbol{\theta} (\tau^\prime) \right]} \nabla_{\boldsymbol{\theta}} r_\boldsymbol{\theta} (\tau) \right]\]where $q(\tau)$ is some easy-to-compute trajectory distribution that we can draw samples from, and $w_\boldsymbol{\theta} (\tau) = \left( \exp r_\boldsymbol{\theta} (\tau) \right) / q (\tau)$.
Optimization of $q(\tau)$ via Guided Policy Search
The key component of guided cost learning is that the sampling distribution $q(\tau)$ can be iteratively updated to approximate the optimal sampling distribution $p_\boldsymbol{\theta} (\tau)$ without needing to compute $p_\boldsymbol{\theta} (\tau)$. This is achieved through guided policy search (GPS)-based optimization.
Note that the distribution $p_\boldsymbol{\theta} (\tau)$ captures high-reward regions with respect to $r_\boldsymbol{\theta}$, but does not account for the current policy $q(\tau)$. Guided policy search adapts the current policy $q (\tau)$ towards regions with higher rewards using the guidance of $p_{\boldsymbol{\theta}} (\tau)$. Specifically, after each reward function update, the sampling policy $q(\tau)$ is updated to align with $p_\boldsymbol{\theta}$ by minimizing the KL divergence, or equivalently, by maximizing the entropy-regularized return:
\[\begin{aligned} \min_q \mathcal{L}_\texttt{sampler} (q) & = \min_q \mathrm{KL} (q( \tau ) \Vert p_\boldsymbol{\theta} (\tau)) \equiv \min_q \mathbb{E}_{\tau \sim q} \left[ \log \frac{q (\tau)}{ p_\boldsymbol{\theta} (\tau) } \right] \\ & = \min_q \left\{ \mathbb{E}_{\tau \sim q} \left[ \log q (\tau) \right] - \mathbb{E}_{\tau \sim q} \left[ r_\boldsymbol{\theta} (\tau) \right] + \log Z (\boldsymbol{\theta}) \right\} \\ & = \max_q \left\{ \mathbb{E}_{\tau \sim q} \left[ r_\boldsymbol{\theta} (\tau) \right] + \mathbb{H} (q) \right\} \end{aligned}\]Consequently, this training procedure yields both a learned cost function, characterizing the distribution of demonstrations $\mathcal{D}$, and a learned policy $q(\tau)$, capable of generating samples from the demonstration distribution.
GAN-Guided Cost Learning (GAN-GCL)
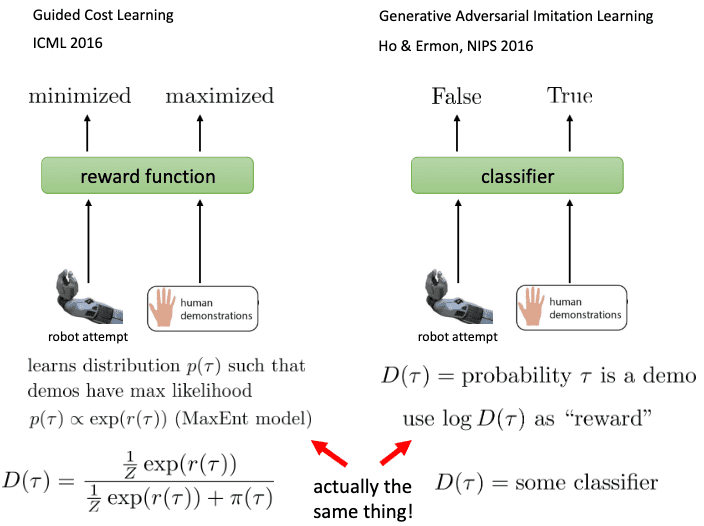
The connections between GANs and IRL are first demonstrated in Finn et al. 2016, which introduces an algorithm called generative adversarial network guided cost learning (GAN-GCL). This algorithm utilizes the GAN training process to theoretically achieve the same behavior as guided cost learning.
Mixture of Demonstration and Sampling Policy
The first step towards achieving equivalence is modifying the sampling distribution $q(\tau)$. In guided cost learning, the importance sampling estimate can exhibit high variance if $q (\tau)$ fails to cover some trajectories $\tau$ with high values of $\exp (r_\boldsymbol{\theta} (\tau))$. This issue can be mitigated by mixing the demonstration data samples from $\mathcal{D}$ with generated samples from $q(\tau)$:
\[\begin{aligned} \mathcal{L}_{\texttt{reward}} (\boldsymbol{\theta}) & = \mathbb{E}_{\tau \sim p_\mathcal{D}} \left[ \log p_\boldsymbol{\theta} (\tau) \right] = \mathbb{E}_{\tau \sim p_\mathcal{D}} \left[ r_\boldsymbol{\theta} (\tau) \right] - \log Z (\boldsymbol{\theta}) \\ & = \mathbb{E}_{\tau \sim p_\mathcal{D}} \left[ \log p_\boldsymbol{\theta} (\tau) \right] = \mathbb{E}_{\tau \sim p_\mathcal{D}} \left[ r_\boldsymbol{\theta} (\tau) \right] - \log \mathbb{E}_{\tau \sim \mu} \left[ \frac{\exp (r_\boldsymbol{\theta} (\tau))}{\frac{1}{2} \tilde{p} (\tau) + \frac{1}{2} q (\tau)} \right] \end{aligned}\]where $\mu = \frac{1}{2} p_\mathcal{D} + \frac{1}{2} q$ is the sampling distribution and $\frac{1}{2} \tilde{p} (\tau) + \frac{1}{2} q (\tau)$ is an importance weight. Here, $\tilde{p} (\tau)$ is a rough estimate for the expert trajectory distribution $p_\mathcal{D} (\tau)$; for example, we could use the current model $p_\boldsymbol{\theta}$, or a simpler density model trained by another method.
Equivalence between GANs and GCL
Recall that the optimal discriminator of GAN is given by
\[D^* (\tau) = \frac{p (\tau)}{p (\tau) + q_\boldsymbol{\psi} (\tau)}\]for a fixed generator with density $q_\boldsymbol{\psi} (\tau)$ where $p(\tau)$ is the distribution of the real data. In the traditional GAN algorithm, the discriminator is trained to directly output this value. When the generator density $q_\boldsymbol{\psi} (\tau)$ can be evaluated, the discriminator $D_\boldsymbol{\theta}$ can be used to estimate $p(τ)$, filling in the value of $q(\tau)$ with its known value, instead of having the discriminator estimate $D^*$ directly:
\[D_\boldsymbol{\theta} (\tau) = \frac{p_\boldsymbol{\theta} (\tau)}{p_\boldsymbol{\theta} (\tau) + q_\boldsymbol{\psi} (\tau)}\]To build a connection to Max-Ent IRL, we replace the expert trajectory distribution $p_\boldsymbol{\theta} (\tau)$ with the energy-based model:
\[\begin{aligned} D_\boldsymbol{\theta} (\tau) = \frac{\frac{1}{Z (\boldsymbol{\theta})} \exp r_\boldsymbol{\theta} (\tau)}{\frac{1}{Z (\boldsymbol{\theta})} \exp r_\boldsymbol{\theta} (\tau) + q_\boldsymbol{\psi} (\tau)} = \texttt{sigmoid} \left( r_\boldsymbol{\theta} (\tau) - \log Z (\boldsymbol{\theta}) - \log q_\boldsymbol{\psi} (\tau) \right) \end{aligned}\]where the resulting architecture is very similar to a simple binary classifier, with a sigmoid as the final layer. The only adjustment here is to subtract $\log Z (\boldsymbol{\theta})$ and $\log q(\tau)$ from the input to the sigmoid.
Then, the discriminator loss $\mathcal{L}_{D}$ can be rewritten as:
\[\require{cancel} \begin{aligned} \mathcal{L}_D (\boldsymbol{\theta}) & = - \mathbb{E}_{\tau \sim q_\boldsymbol{\psi}} \left[ \log ( 1 - D_\boldsymbol{\theta} ( \tau ) ) \right] - \mathbb{E}_{\tau \sim p_\texttt{data}} \left[ \log D (\tau) \right] \\ & = \mathbb{E}_{\tau \sim q_\boldsymbol{\psi}} \left[ - \log \frac{q_\boldsymbol{\psi} (\tau)}{2 \tilde{\mu} (\tau)}\right] + \mathbb{E}_{\tau \sim p_\texttt{data}} \left[ - \log \frac{\frac{1}{Z (\boldsymbol{\theta})} \exp r_\boldsymbol{\theta} (\tau)}{2 \tilde{\mu} (\tau)} \right] \\ & \mathbb{E}_{\tau \sim p_\texttt{data}} \left[ - r_\boldsymbol{\theta} (\tau) + \log Z (\boldsymbol{\theta}) \right] + 2 \mathbb{E}_{\tau \sim \mu} \left[ \log \tilde{\mu} (\tau) \right] + \cancel{2 \log 2} \end{aligned}\]where $\mu = \frac{1}{2} (p_\texttt{data} + q_\boldsymbol{\psi})$ and $\tilde{\mu} = \frac{1}{2} (p_\boldsymbol{\theta} + q_\boldsymbol{\psi})$. And similarly for generator loss $\mathcal{L}_{G}$, we obtain:
\[\require{cancel} \begin{aligned} \mathcal{L}_G (\boldsymbol{\psi}) & = \mathbb{E}_{\tau \sim q_\boldsymbol{\psi}} \left[ - \log D_\boldsymbol{\theta} (\tau) \right] \\ & = \mathbb{E}_{\tau \sim q_\boldsymbol{\psi}} \left[ - \log \frac{\frac{1}{Z(\boldsymbol{\theta})} \exp r_\boldsymbol{\theta} (\tau)}{q_\boldsymbol{\psi} (\tau)} \right] \\ & = - \mathbb{E}_{\tau \sim q_\boldsymbol{\psi}} \left[ r_\boldsymbol{\theta} (\tau) \right] - \mathbb{H} (q_\boldsymbol{\psi}) + \cancel{\log Z (\boldsymbol{\theta})} \end{aligned}\]This gives the following relationship between GCL and GAN minimization losses:
\[\begin{aligned} \texttt{GCL: } & \begin{aligned}[t] \mathcal{L}_\texttt{reward} & = \mathbb{E}_{\tau \sim p_\mathcal{D}} \left[ - r_\boldsymbol{\theta} (\tau) \right] + \log \mathbb{E}_{\tau \sim \mu} \left[ \frac{\exp (r_\boldsymbol{\theta} (\tau))}{\frac{1}{2} \tilde{p} (\tau) + \frac{1}{2} q (\tau)} \right] \\ \mathcal{L}_\texttt{sampler} & = - \mathbb{E}_{\tau \sim q} \left[ r_\boldsymbol{\theta} (\tau) \right] - \mathbb{H} (q) \end{aligned} \\ \texttt{GAN: } & \begin{aligned}[t] \mathcal{L}_D (\boldsymbol{\theta}) & = \mathbb{E}_{\tau \sim p_\texttt{data}} \left[ - r_\boldsymbol{\theta} (\tau) + \log Z (\boldsymbol{\theta}) \right] + 2 \mathbb{E}_{\tau \sim \mu} \left[ \log \tilde{\mu} (\tau) \right] \\ \mathcal{L}_G (\boldsymbol{\psi}) & = \mathbb{E}_{\tau \sim q_\boldsymbol{\psi}} \left[ - r_\boldsymbol{\theta} (\tau) \right] - \mathbb{H} (q_\boldsymbol{\psi}) \\ \end{aligned} \end{aligned}\]and we can observe that \(\mathcal{L}_G (\boldsymbol{\psi})\) and \(\mathcal{L}_\texttt{sampler}\) are equivalent.
Equivalence between $\mathcal{L}_\texttt{reward}$ and $\mathcal{L}_D$
To build the equivalence between the MaxEnt IRL loss and the discriminator loss, we can establish the following facts:
- The value of $Z (\boldsymbol{\theta})$ which minimizes $\mathcal{L}_D$ is an importance-sampling estimator for the partition function of $\mathcal{L}_{\texttt{reward}}$
At the minimizing value of $Z (\boldsymbol{\theta})$, the derivative of these term with respect to $Z$ will be zero: $$ \begin{aligned} \frac{\partial \mathcal{L}_D}{\partial Z (\boldsymbol{\theta})} = 0 \implies \frac{1}{Z (\boldsymbol{\theta})} & = \mathbb{E}_{\tau \sim \mu}\left[{ \frac{ \frac{1}{Z(\boldsymbol{\theta})^2} \exp(r_\boldsymbol{\theta} (\tau))}{\tilde{\mu}(\tau)}}\right] \\ \therefore Z (\boldsymbol{\theta}) & = \mathbb{E}_{\tau \sim \mu} \left[\frac{\exp(r_\boldsymbol{\theta} (\tau))}{\tilde{\mu}(\tau)}\right] \end{aligned} $$ - $\mathcal{L}_D$ has the same derivative as $\mathcal{L}_{\texttt{reward}}$
The following equalities for the derivative of $\mathcal{L}_D$ w.r.t. parameters $\boldsymbol{\theta}$ hold: $$ \require{cancel} \begin{aligned} \nabla_\boldsymbol{\theta} \mathcal{L}_D (\boldsymbol{\theta} ) & = \mathbb{E}_{\tau \sim p_\texttt{data}} \left[ - \nabla_\boldsymbol{\theta} r_\boldsymbol{\theta} (\tau) \right] + \nabla_\boldsymbol{\theta} \log Z (\boldsymbol{\theta}) + 2 \mathbb{E}_{\tau \sim \mu} \left[ \nabla_\boldsymbol{\theta} \log \tilde{\mu} (\tau) \right] \\ & = \mathbb{E}_{\tau \sim p_\texttt{data}} \left[ - \nabla_\boldsymbol{\theta} r_\boldsymbol{\theta} (\tau) \right] + \nabla_\boldsymbol{\theta} \log Z (\boldsymbol{\theta}) + \mathbb{E}_{\tau \sim \mu} \left[ \frac{\nabla_\boldsymbol{\theta} p_\boldsymbol{\theta} (\tau)}{\tilde{\mu} (\tau)} \right] \\ & = \mathbb{E}_{\tau \sim p_\texttt{data}} \left[ - \nabla_\boldsymbol{\theta} r_\boldsymbol{\theta} (\tau) \right] + \cancel{\frac{\nabla_\boldsymbol{\theta} Z (\boldsymbol{\theta})}{Z (\boldsymbol{\theta})}} - \cancel{\mathbb{E}_{\tau \sim \mu} \left[ \frac{ \frac{\nabla_\boldsymbol{\theta} Z (\boldsymbol{\theta})}{Z (\boldsymbol{\theta})^2} \exp (r_\boldsymbol{\theta} (\tau))}{\tilde{\mu} (\tau)} \right]} + \mathbb{E}_{\tau \sim \mu} \left[ \frac{p_\boldsymbol{\theta} (\tau) \cdot \nabla_\boldsymbol{\theta} r_\boldsymbol{\theta} (\tau)}{\tilde{\mu} (\tau)} \right] \\ & = \nabla_\boldsymbol{\theta} \mathcal{L}_\texttt{reward} (\boldsymbol{\theta} ) \end{aligned} $$ where we didn't differentiate the importance weight $\tilde{\mu}$ in $\mathcal{L}_\texttt{reward} (\boldsymbol{\theta} )$ and used the definition of $Z (\boldsymbol{\theta})$ as an importance sampling estimate for the equalities: $$ \begin{aligned} \frac{1}{Z (\boldsymbol{\theta})} & = \mathbb{E}_{\tau \sim \mu}\left[{ \frac{ \frac{1}{Z(\boldsymbol{\theta})^2} \exp(r_\boldsymbol{\theta} (\tau))}{\tilde{\mu}(\tau)}}\right] \\ \implies \frac{\nabla_\boldsymbol{\theta} Z (\boldsymbol{\theta})}{Z (\boldsymbol{\theta})} & = \mathbb{E}_{\tau \sim \mu}\left[{ \frac{ \frac{\nabla_\boldsymbol{\theta} Z (\boldsymbol{\theta})}{Z(\boldsymbol{\theta})^2} \exp(r_\boldsymbol{\theta} (\tau))}{\tilde{\mu}(\tau)}}\right] \\ \text{ and } Z (\boldsymbol{\theta}) & = \mathbb{E}_{\tau \sim \mu} \left[\frac{\exp(r_\boldsymbol{\theta} (\tau))}{\tilde{\mu}(\tau)}\right] \end{aligned} $$
Generative Adversarial Imitation Learning (GAIL)
Concurrently with GAN-GCL, Ho et al. NIPS 2016 draws an analogy between imitation learning (recovering the expert’s reward with IRL, and then extracting a policy from that reward from RL) and GAN, proposing an algorithm called generative adversarial imitation learning (GAIL).
Preliminary: Maximum Causal Entropy (MCE) IRL
In stochastic MDP (i.e., \(\mathbb{P}_\mathcal{S} (\mathbf{s}^\prime \vert \mathbf{s}, \mathbf{a}) > 0\)), the original Max-Ent IRL calculates the entropy over the entire trajectory distribution, incorporating an undesirable dependence on transition dynamics through terms $\mathbb{H} (\mathbb{P}_\mathcal{S})$:
\[\begin{aligned} \mathbb{H} \left( p ( \mathbf{s}_{0:T-1}, \mathbf{a}_{0:T-1}, \vert \mathbf{R}) \right) & =\sum_{t=0}^{T-1} \mathbb{H} \left( p (\mathbf{s}_t, \mathbf{a}_t \mid \mathbf{s}_{0: t-1}, \mathbf{a}_{0: t-1}) \right) & \because \textrm{ chain rule } \\ & =\sum_{t=0}^{T-1} \mathbb{H} \left( p (\mathbf{s}_t \mid \mathbf{s}_{0: t-1}, \mathbf{a}_{0: t-1}) \right)+\sum_{t=0}^{T-1} \mathbb{H} \left( p( \mathbf{a}_t \mid \mathbf{s}_{0: t}, \mathbf{a}_{0: t-1}) \right) & \because \textrm{ chain rule } \\ & =\sum_{t=0}^{T-1} \mathbb{H} \left( p (\mathbf{s}_t \mid \mathbf{s}_{t-1}, \mathbf{a}_{t-1}) \right)+\sum_{t=0}^{T-1} \mathbb{H} \left( p (\mathbf{a}_t \mid \mathbf{s}_t ) \right) & \because \text{ Markov property } \\ & =\sum_{t=0}^{T-1} \underbrace{\mathbb{H} \left( \mathbb{P}_\mathcal{S} \right)}_{\text {state transition entropy}}+\underbrace{\mathbb{H} \left( \mathbf{a}_{0: T-1} \Vert \mathbf{s}_{0: T-1}\right)}_{\text {causal entropy }} \end{aligned}\]Maximizing Shannon entropy therefore introduces a bias towards selecting actions with uncertain, and possibly risky, outcomes. Consequently, maximum causal entropy (MCE) IRL is to be favored over maximum Shannon entropy IRL in stochastic MDPs. It is important to noting that MCE IRL reduces into the original Max-Ent IRL for deterministic MDP cases.
Causal entropy: $$ \mathbb{H} (\mathbf{a}^T \Vert \mathbf{s}^T) \equiv \mathbb{E}_\pi \left[ - \log p (\mathbf{a}^T \Vert \mathbf{s}^T) \right] = \sum_{t=0}^{T-1} \mathbb{H}(\mathbf{a}_t \vert \mathbf{s}_{1:t}, \mathbf{a}_{1:t-1}) $$ measures the uncertainty present in the causally conditioned distribution: $$ p(\mathbf{a}^T \vert \mathbf{s}^T) \equiv \prod_{t=1}^{T-1} p (\mathbf{a}_t \vert \mathbf{s}_{1:t}, \mathbf{a}_{1:t-1}) = \prod_{t=1}^{T-1} \pi (\mathbf{a}_t \vert \mathbf{s}_t) \; \text{on MDP} $$
Consequently, the MCE IRL problem can be formulated as:
\[\begin{aligned} \texttt{MCE IRL: } p^* (\mathbf{a}_t \vert \mathbf{s}_{1:t}, \mathbf{a}_{1:t-1}) & = \underset{p}{\arg \max} \; \mathbb{H} (\mathbf{a}^T \Vert \mathbf{s}^T) \\ & \text{ s.t. } \begin{aligned}[t] & \mathbb{E}_{\mathbf{s}_{t + 1} \sim \mathbb{P}_\mathcal{S} (\cdot \vert \mathbf{s}_t, \mathbf{a}_t), \mathbf{a}_t \sim p (\cdot \vert \mathbf{s}_{1:t}, \mathbf{a}_{1:t-1})} \left[ \sum_{t=0}^{T-1} \gamma^t r_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t) \right] = \mathbb{E}_{\pi^*} \left[ \sum_{t=0}^{T-1} \gamma^t r_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t) \right] \\ & \int p (\mathbf{a}_t \vert \mathbf{s}_{1:t}, \mathbf{a}_{1:t-1}) d \mathbf{a}_t = 1 \text{ and } p (\mathbf{a}_t \vert \mathbf{s}_{1:t}, \mathbf{a}_{1:t-1}) \geq 0 \; \forall \tau \in \mathcal{D} \end{aligned} \end{aligned}\]Note that under the MDP environment, \(p^* (\mathbf{a}_t \vert \mathbf{s}_{1:t}, \mathbf{a}_{1:t-1})\) can be replaced by \(p^* (\mathbf{a}_t \vert \mathbf{s}_t)\). Then, we have the following auxiliary loss:
\[\begin{aligned} \mathcal{L}_{\texttt{MCE}} (\boldsymbol{\theta}) & = \underset{\pi}{\max} \left\{ \mathbb{H} (\pi) + \mathbb{E}_{\pi} \left[ r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{\pi^*} \left[ r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \right] \right\} \\ & = \underset{\pi}{\max} \left\{ \mathbb{H} (\pi) + \mathbb{E}_{\pi} \left[ r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \right] \right\} - \mathbb{E}_{\pi^*} \left[ r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \right] \end{aligned}\]where we denotes:
\[\begin{aligned} \mathbb{E}_{\pi} \left[ r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \right] & = \mathbb{E}_{\mathbf{s}_{t + 1} \sim \mathbb{P}_\mathcal{S} (\cdot \vert \mathbf{s}_t, \mathbf{a}_t), \mathbf{a}_t \sim \pi (\cdot \vert \mathbf{s}_t)} \left[ \sum_{t=0}^{T-1} \gamma^t r_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t) \right] \\ \mathbb{H} (\pi) & = \mathbb{H} (\mathbf{a}^T \Vert \mathbf{s}^T) = \mathbb{E}_\pi \left[ - \log \left(\prod_{t=1}^{T-1} \pi (\mathbf{a}_t \vert \mathbf{s}_t) \right) \right] \end{aligned}\]for brevity. For more details of MCE IRL, please refer to my previous post.
Since this optimization is performed under a finite expert demonstrations $\mathcal{D}$, we may introduce convex regularizer $\psi: \mathbb{R}^{\mathcal{S} \times \mathcal{A}} \to \mathbb{R}$ to avoid the overfitting, which are easy to optimize due to its convexity:
\[\mathcal{L}_{\texttt{MCE}} (\boldsymbol{\theta}) = \underset{\pi}{\max} \left\{ \mathbb{H} (\pi) + \mathbb{E}_{\pi} \left[ r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \right] \right\} - \mathbb{E}_{\pi^*} \left[ r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \right] + \color{red}{\psi (r_\boldsymbol{\theta})}\]Preliminary: Occupancy Measure
To transform optimization problems over policies into convex problems, we will use the notion of occupancy measure in the GAIL formulation:
For a policy $\pi \in \Pi$, we define the occupancy measure $\rho_\pi: \mathcal{S} \times \mathcal{A} \to \mathbb{R}$ as the $\gamma$-discounted state-action visitation distribution of $\pi$: $$ \rho_\pi (\mathbf{s}, \mathbf{a}) = \pi (\mathbf{a} \vert \mathbf{s}) \sum_{t=0}^\infty \gamma^t \mathbb{P}(\mathbf{s}_t = \mathbf{s} \vert \pi) $$ Define the set of valid occupancy measures $\mathcal{P} = \{ \rho_\pi \vert \pi \in \Pi \}$. Note that there is a one-to-one correspondence between $\Pi$ and $\mathcal{P}$: $$ \pi_\rho (\mathbf{a} \vert \mathbf{s}) = \frac{\rho (\mathbf{s}, \mathbf{a})}{\sum_{\mathbf{a}^\prime \in \mathcal{A}} \rho (\mathbf{s}, \mathbf{a}^\prime)} $$ Therefore, $\pi = \pi_{\rho_\pi}$.
Furthermore, it allows us to write:
\[\begin{aligned} \mathbb{E}_{\pi} \left[ r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \right] & = \sum_{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}} \rho_\pi (\mathbf{s}, \mathbf{a}) r_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) \\ \mathbb{H}(\pi) & = \bar{\mathbb{H}} (\rho_\pi) \text{ where } \bar{\mathbb{H}} (\rho) \equiv - \sum_{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}} \rho (\mathbf{s}, \mathbf{a}) \log \pi_\rho (\mathbf{a} \vert \mathbf{s}) \end{aligned}\]And this leads to an equivalent of $\mathcal{L}_{\texttt{MCE}}$:
\[\begin{aligned} \mathcal{L}_{\texttt{MCE}} (r) & = \underset{\pi}{\max} \left\{ \mathbb{H} (\pi) + \mathbb{E}_{\pi} \left[ r (\mathbf{s}, \mathbf{a}) \right] \right\} - \mathbb{E}_{\pi^*} \left[ r (\mathbf{s}, \mathbf{a}) \right] \\ & = \underset{\pi}{\max} \left\{ \bar{\mathbb{H}} (\rho_\pi) - \sum_{\mathbf{s}, \mathbf{a} \in \mathcal{S} \times \mathcal{A}} \left( \rho_{\pi^*} - \rho_{\pi} \right) \cdot r (\mathbf{s}, \mathbf{a}) \right\} \end{aligned}\]Characterizing the induced optimal policy
Let $\mathrm{RL}(r)$ represent the policy learned by a RL algorithm with the reward function $r$, and \(\mathrm{IRL} (\pi^*)\) denote the reward function extracted by MCE IRL from the expert policy $\pi^*$. To establish the equivalence between GANs and imitation learning, we first characterize the policies obtained via the alternation of RL and IRL algorithms.
$\mathbf{Proof.}$
Let $\tilde{r} \in \mathrm{IRL}_\psi (\pi^*)$, $\tilde{\pi} \in \mathrm{RL}(\tilde{r})$, and:
\[\begin{aligned} \pi_A & \in \underset{\pi}{\arg \min} \; \left\{ - \mathbb{H}(\pi) + \psi^* (\rho_\pi - \rho_{\pi^*}) \right\} \\ & = \underset{\pi}{\arg \min} \; \max_{r} \left\{ - \mathbb{H}(\pi) + \sum_{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}} ( \rho_\pi - \rho_{\pi^*}) \cdot r (\mathbf{s}, \mathbf{a}) + \psi (r) \right\} \end{aligned}\]We will show that $\pi_A = \tilde{\pi}$. Let $\rho_A$ and $\tilde{\rho}$ be the occupancy measure of $\pi_A$ and $\tilde{\pi}$, respectively. Define $\bar{\mathcal{L}}: \mathcal{P} \times \mathbb{R}^{\mathcal{S} \times \mathcal{A}} \to \mathbb{R}$ by:
\[\bar{\mathcal{L}} (\rho, r) = - \bar{\mathbb{H}}(\rho) - \psi (r) + \sum_{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}} (\rho - \rho_{\pi^*}) \cdot r (\mathbf{s}, \mathbf{a})\]Then, from the one-to-one correspondence $\pi = \rho_{\pi_\rho}$ and the definition of $\bar{\mathbb{H}} (\rho)$:
\[\bar{\mathbb{H}} (\rho) = - \sum_{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}} \rho (\mathbf{s}, \mathbf{a}) \log \pi_\rho (\mathbf{a} \vert \mathbf{s})\]we obtain \(\mathcal{L}_{\texttt{MCE}} (r) = \max_{\rho \in \mathcal{P}} \bar{\mathcal{L}}(\rho, r)\) and:
\[\begin{aligned} \rho_A & \in \underset{\rho \in \mathcal{P}}{\arg \min} \; \max_{r} \bar{\mathcal{L}} (\rho, r) \\ \tilde{r} & \in \underset{r}{\arg \max} \; \min_{\rho \in \mathcal{P}} \bar{\mathcal{L}} (\rho, r) \\ \tilde{rho} & \in \underset{\rho \in \mathcal{P}}{\arg \min} \; \bar{\mathcal{L}} (\rho, \tilde{r}) \\ \end{aligned}\]Since the Shannon entropy $\mathbb{H}$ is concave and $\psi$ is convex, $\bar{\mathcal{L}} (\rho, \cdot)$ is convex and $\bar{\mathcal{L}} (\cdot, r)$ is concave. By minimax theorem, we have:
\[\min_{\rho \in \mathcal{P}} \max_{r} \bar{\mathcal{L}} (\rho, r) = \max_{r} \min_{\rho \in \mathcal{P}} \bar{\mathcal{L}} (\rho, r)\]This implies $\rho_A = \tilde{\rho}$ and thus $\pi_A = \tilde{\pi}$.
\[\tag*{$\blacksquare$}\]In other words, if there were no cost regularization, the recovered policy would precisely match the expert’s occupancy measure:
$\mathbf{Proof.}$
Define $\bar{\mathcal{L}}: \mathcal{P} \times \mathbb{R}^{\mathcal{S} \times \mathcal{A}} \to \mathbb{R}$ by:
\[\bar{\mathcal{L}} (\rho, r) = - \bar{\mathbb{H}}(\rho) + \sum_{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}} (\rho - \rho_{\pi^*}) \cdot r (\mathbf{s}, \mathbf{a})\]It is trivial that $\min_r \max_{\rho \in \mathcal{P}} \bar{\mathcal{L}} (\rho, r)$ is the dual of the following primal optimization:
\[\begin{array}{cl} \max_{\rho} & \bar{\mathbb{H}} (\rho) \\ \textrm{ s.t. } & \rho (\mathbf{s}, \mathbf{a}) = \rho_{\pi^*} (\mathbf{s}, \mathbf{a}) \quad \forall (\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A} \end{array}\]and $\tilde{r}$ is the dual optimum.
Note that the inner product with constant vectors is convex due to linearity. Therefore, if we can prove that $-\bar{\mathbb{H}}$ is in strictly convex, $\bar{\mathcal{L}} (\cdot, \tilde{r})$ is then strict convex and the uniqueness of global minimizer is guaranteed.
Then, by strong duality, or Slater’s condition if the solution $\tilde{\rho}$ of the primal problem is feasible, i.e. \(\tilde{\rho} = \rho_{\pi^*}\), it must be the optimal solution of the primal problem. This implies that \(\rho_{\tilde{\pi}} = \tilde{\rho} = \rho_{\pi^*}\).
And we can show that $\bar{\mathbb{H}}$ is in strictly concave; $\bar{\mathbb{H}} (\lambda \rho + (1-\lambda) \rho^\prime) \geq \lambda \bar{\mathbb{H}} (\rho) + (1-\lambda) \bar{\mathbb{H}} (\rho^\prime)$:
\[\begin{aligned} - &(\lambda \rho(\mathbf{s}, \mathbf{a}) + (1-\lambda)\rho'(\mathbf{s}, \mathbf{a}) )\log \frac{\lambda \rho(\mathbf{s}, \mathbf{a}) + (1-\lambda)\rho'(\mathbf{s}, \mathbf{a}) }{\sum_{\mathbf{a}'}(\lambda \rho(\mathbf{s}, \mathbf{a}') + (1-\lambda)\rho'(\mathbf{s}, \mathbf{a}') )} \\ &= -(\lambda \rho(\mathbf{s}, \mathbf{a}) + (1-\lambda)\rho'(\mathbf{s}, \mathbf{a}) )\log \frac{\lambda \rho(\mathbf{s}, \mathbf{a}) + (1-\lambda)\rho'(\mathbf{s}, \mathbf{a}) }{\lambda \sum_{\mathbf{a}'}\rho(\mathbf{s}, \mathbf{a}') + (1-\lambda)\sum_{\mathbf{a}'}\rho'(\mathbf{s}, \mathbf{a}')} \\ &\geq -\lambda \rho(\mathbf{s}, \mathbf{a})\log\frac{\lambda\rho(\mathbf{s}, \mathbf{a})}{\lambda\sum_{\mathbf{a}'}\rho(\mathbf{s}, \mathbf{a}')} - (1-\lambda)\rho'(\mathbf{s}, \mathbf{a})\log\frac{(1-\lambda)\rho'(\mathbf{s}, \mathbf{a})}{(1-\lambda)\sum_{\mathbf{a}'}\rho'(\mathbf{s}, \mathbf{a}')} \\ &= \lambda \left(-\rho(\mathbf{s}, \mathbf{a})\log\frac{\rho(\mathbf{s}, \mathbf{a})}{\sum_{\mathbf{a}'}\rho(\mathbf{s}, \mathbf{a}')}\right) + (1-\lambda)\left(-\rho'(\mathbf{s}, \mathbf{a})\log\frac{\rho'(\mathbf{s}, \mathbf{a})}{\sum_{\mathbf{a}'}\rho'(\mathbf{s}, \mathbf{a}')}\right), \end{aligned}\]with equality if and only if $\pi_\rho = \pi_{\rho’}$, which is equivalent to $\rho = \rho’$ due to the one-to-one correspondence.
Consequently, from the corollary, we can deduce that:
- IRL is the dual of an occupancy measure matching problem, and the recovered reward function represents the dual optimum.
- The induced optimal policy, obtained by running RL after IRL, is the optimum of the primal problem (occupancy measure matching problem).
Algorithm: GAN-based Instantiation
The above corollary is not practically useful since the expert trajectory distribution is unknown and only available as a finite set of samples. Exact occupancy measure with limited data also cause the learned policy to advoid visiting some unseen state-action pairs never visited the expert. Therefore, we can relax the primal problem of the corollary into the form of the proposition:
\[\begin{gathered} \begin{array}{cl} \max_{\rho} & \bar{\mathbb{H}} (\rho) \\ \textrm{ s.t. } & \rho (\mathbf{s}, \mathbf{a}) = \rho_{\pi^*} (\mathbf{s}, \mathbf{a}) \quad \forall (\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A} \end{array} \\ \Downarrow \\ \max_{\pi \in \Pi} \; \mathbb{H}(\pi) - \psi^* (\rho_{\pi^*} - \rho_\pi) \end{gathered}\]The authors draw an analogy between $\mathrm{RL} \circ \mathrm{IRL}$ and GAN from the choice of $\psi$:
\[\psi_\mathrm{GA}^* (\rho_\pi - \rho_{\pi^*}) = \max_{D \in (0, 1)^{\mathcal{S} \times \mathcal{A}}} \mathbb{E}_\pi \left[ \log D (\mathbf{s}, \mathbf{a}) \right] + \mathbb{E}_{\pi^*} \left[ \log (1 - D (\mathbf{s}, \mathbf{a})) \right]\]which is exactly the discriminator objective in GANs, where $D: \mathcal{S} \times \mathcal{A} \to (0, 1)$. Notably, this loss amounts to the Jensen-Shannon divergence \(\mathrm{JSD}(\pi, \pi^*)\) at the optimal discriminator \(D^* = \frac{\pi^*}{\pi^* + \pi}\):
\[\begin{aligned} \psi_\mathrm{GA}^* (\rho_{\pi^*} - \rho_\pi) & = \mathbb{E}_\pi \left[\log \frac{\pi(\mathbf{s}, \mathbf{a})}{\pi(\mathbf{s}, \mathbf{a})+\pi^*(\mathbf{s}, \mathbf{a})} \right] + \mathbb{E}_{\pi^*} \left[\log \frac{\pi^*}{\pi(\mathbf{s}, \mathbf{a})+\pi^*(\mathbf{s}, \mathbf{a})} \right] \\ & = \mathbb{E}_\pi \left[\log \frac{\pi(\mathbf{s}, \mathbf{a})}{\frac{1}{2} (\pi(\mathbf{s}, \mathbf{a})+\pi^*(\mathbf{s}, \mathbf{a}))} \right] + \mathbb{E}_{\pi^*} \left[\log \frac{\pi^*}{\frac{1}{2} (\pi(\mathbf{s}, \mathbf{a})+\pi^*(\mathbf{s}, \mathbf{a}))} \right] - 2 \log 2 \\ & = 2 \cdot \mathrm{JSD}(\pi, \pi^*) - 2\log 2 \end{aligned}\]Ultimately, the final objective of the GAIL algorithm is given by:
\[\begin{gathered} \mathcal{L}_{\texttt{GAIL}} (\boldsymbol{\theta}, D) = \mathbb{E}_\pi \left[ \log D (\mathbf{s}, \mathbf{a}) \right] + \mathbb{E}_{\pi^*} \left[ \log (1 - D (\mathbf{s}, \mathbf{a})) \right] - \lambda \mathbb{H}(\pi) \\ \text{ where } \quad \pi^*, D^* = \underset{\pi \in \Pi}{\arg \min} \; \underset{D \in (0, 1)^{\mathcal{S} \times \mathcal{A}}}{\arg \max} \; \mathcal{L}_{\texttt{GAIL}} (\pi, D) \end{gathered}\]Practically, the GAIL loss is optimized by alternating the gradient ascent for the discriminator $D$ and TRPO step for the policy $\pi$ by interpreting $\log D (\mathbf{s}, \mathbf{a})$ as a reward function.

For the validity of the algorithm, recall that we require the convexity of $\psi_{\mathrm{GA}}$:
$\mathbf{Proof.}$
By setting the discriminator network as a sigmoid classifier:
\[D (\mathbf{s}, \mathbf{a}) = \frac{1}{1 + e^{-f (\mathbf{s}, \mathbf{a})}}\]and using the logistic loss $\phi(x) = \log (1 + e^{-x})$, we have:
\[\begin{aligned} \psi_\mathrm{GA}^* (\rho_{\pi^*} - \rho_\pi) & = \sum_{\mathbf{s}, \mathbf{a}} \max_{D} \rho_\pi \log (1 - D) + \rho_{\pi^*} \log D \\ & = \sum_{\mathbf{s}, \mathbf{a}} \max_{D} \rho_\pi \log \frac{1}{1 + e^f} + \rho_{\pi^*} \log \frac{1}{1 + e^{-f}} \\ & = \sum_{\mathbf{s}, \mathbf{a}} \max_{f} \left\{ - \rho_\pi \phi(f) - \rho_{\pi^*} \phi (-f) \right\} \\ & = \sum_{\mathbf{s}, \mathbf{a}} \max_{f} \left\{ - \rho_\pi \phi(f) - \rho_{\pi^*} \phi (-\phi^{-1} (\phi (f))) \right\} \\ & = \sum_{\mathbf{s}, \mathbf{a}} \max_{\gamma} \left\{ - \rho_\pi \gamma - \rho_{\pi^*} \phi (-\phi^{-1} (\gamma)) \right\} \text{ where } \gamma = \phi (f) \\ & = \sum_{\mathbf{s}, \mathbf{a}} \max_{\gamma} \left\{ (\rho_{\pi^*} - \rho_\pi) \gamma - \rho_{\pi^*} (\gamma + \phi (-\phi^{-1} (\gamma))) \right\} \\ \end{aligned}\]Note that:
\[1 - D = \frac{1}{e^{\phi(f)}} \in (0, 1) \implies e^{\phi(f)} > 1 \implies \gamma = \phi(f) > 0\]Therefore, it suffices to show the concavity of $\psi$ defined as:
\[\begin{aligned} \psi (\gamma) = \begin{cases} \rho_{\pi^*} g (\gamma) & \text{ if } \gamma > 0 \\ \infty & \text{ otherwise} \end{cases} \quad \text{ where } \quad g (\gamma) = \begin{cases} \gamma + \phi (-\phi^{-1} (\gamma)) & \text{ if } \gamma > 0 \\ \infty & \text{ otherwise } \end{cases} \end{aligned}\]Since $\phi$ is concave, and thus $\phi^{-1}$ is convex, we note that:
\[\begin{aligned} \phi (-\phi^{-1} (\lambda x + (1-\lambda) y)) & \geq \phi ( -\lambda \phi^{-1}(x) - (1-\lambda)\phi^{-1}(y)) \\ \geq & \lambda \phi(-\phi^{-1}(x)) + (1-\lambda) \phi(-\phi^{-1}(y)) \end{aligned}\]Therefore, $\phi(-\phi^{-1} (\gamma))$ is concave and the concavity of $g(\gamma)$ and $\psi (\gamma)$.
\[\tag*{$\blacksquare$}\]Adversarial IRL (AIRL)
In practical imitation learning benchmarks, GAN-GCL often exhibits poor performance since preforming discrimination over entire trajectories $\tau$ can complicate training and result in high variance.
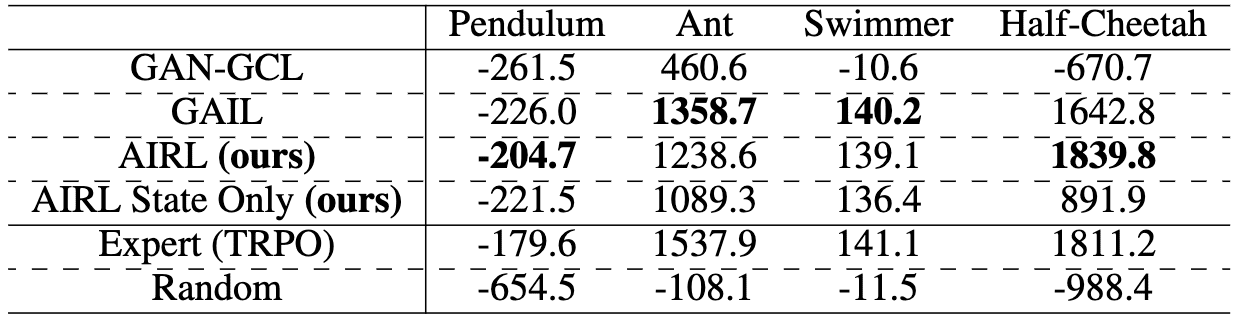
Instead, adversarial IRL (AIRL) introduced by Fu et al. ICLR 2018 discriminates between state-action pairs:
\[\begin{aligned} \texttt{GAN-GCL: } & \; D_\boldsymbol{\theta} (\color{blue}{\tau}) = \frac{\exp f_\boldsymbol{\theta} (\color{blue}{\tau})}{\exp f_\boldsymbol{\theta} (\color{blue}{\tau}) + \pi (\color{blue}{\tau})} \\ \texttt{AIRL: } & \; D_\boldsymbol{\theta} (\color{red}{\mathbf{s}, \mathbf{a}}) = \frac{\exp f_\boldsymbol{\theta} (\color{red}{\mathbf{s}, \mathbf{a}})}{\exp f_\boldsymbol{\theta} (\color{red}{\mathbf{s}, \mathbf{a}}) + \pi (\color{red}{\mathbf{a} \vert \mathbf{s}})} \end{aligned}\]where $f_\boldsymbol{\theta}$ is a reward approximator that also implicitly learns the partition function $Z (\boldsymbol{\theta})$. And the objective of the discriminator is to minimize cross-entropy loss between expert demonstrations and generated samples:
\[\mathcal{L}(\boldsymbol{\theta}) = - \mathbb{E}_\pi \left[ \sum_{t=0}^T \log (1 - D_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t)) \right] - \mathbb{E}_\mathcal{D} \left[ \log D_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t) \right]\]Note that training the gradient of the discriminator objective:
\[\begin{aligned} - \mathcal{L}(\boldsymbol{\theta}) & = \mathbb{E}_\mathcal{D} \left[ \sum_{t=0}^T \log \frac{\exp \left(f_{\boldsymbol{\theta}} (\mathbf{s}_t, \mathbf{a}_t)\right)}{\exp \left(f_{\boldsymbol{\theta}} (\mathbf{s}_t, \mathbf{a}_t) \right) + \pi (\mathbf{a}_t \vert \mathbf{s}_t)} \right] + \mathbb{E}_\pi \left[ \sum_{t=0}^T \log \frac{ \pi (\mathbf{a}_t \vert \mathbf{s}_t)}{\exp \left(f_{\boldsymbol{\theta}} (\mathbf{s}_t, \mathbf{a}_t)\right) + \pi (\mathbf{a}_t \vert \mathbf{s}_t) } \right] \\ & = \sum_{t=0}^T \mathbb{E}_\mathcal{D} \left[ f_{\boldsymbol{\theta}} (\mathbf{s}_t, \mathbf{a}_t) \right] + \mathbb{E}_\pi \left[ \log \pi (\mathbf{a}_t \vert \mathbf{s}_t) \right] - 2 \mathbb{E}_{\mu} \left[ \log \left( \exp \left( f_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t) \right) + \pi (\mathbf{a}_t \vert \mathbf{s}_t) \right) \right] \\ \implies & \; \frac{\partial \mathcal{L}(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \mathbb{E}_\mathcal{D} \left[ \sum_{t=0}^T \frac{\partial f_\boldsymbol{\theta}(\mathbf{s}_t, \mathbf{a}_t)}{\partial \boldsymbol{\theta}} \right] - \mathbb{E}_\mu \left[ \sum_{t=0}^T \frac{\exp \left(f_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t) \right)}{\frac{1}{2} \exp \left(f_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t) \right) + \frac{1}{2} \pi (\mathbf{a}_t \vert \mathbf{s}_t)} \frac{\partial f_\boldsymbol{\theta}(\mathbf{s}_t, \mathbf{a}_t)}{\partial \boldsymbol{\theta}} \right] \end{aligned}\]is still equivalent to optimizing the important sampling gradient of Max-Ent IRL with sampling distribution $\mu = \frac{1}{2} p_\mathcal{D} + \frac{1}{2} \pi$:
\[\begin{aligned} \mathcal{L}_\texttt{reward} (\boldsymbol{\theta}) & = \mathbb{E}_{\mathcal{D}} \left[ - r_\boldsymbol{\theta} (\tau) \right] + \log \mathbb{E}_{\tau \sim \mu} \left[ \frac{\exp (r_\boldsymbol{\theta} (\tau))}{\frac{1}{2} \tilde{p} (\tau) + \frac{1}{2} q (\tau)} \right] \\ \implies & \; \frac{\partial \mathcal{L}_\texttt{reward} (\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \mathbb{E}_\mathcal{D} \left[ \sum_{t=0}^T - \frac{\partial r_\boldsymbol{\theta}(\mathbf{s}_t, \mathbf{a}_t)}{\partial \boldsymbol{\theta}} \right] + \mathbb{E}_\mu \left[ \sum_{t=0}^T \frac{p_\boldsymbol{\theta} (\mathbf{s}_t, \mathbf{a}_t)}{\tilde{\mu} (\mathbf{s}_t, \mathbf{a}_t)} \cdot \frac{\partial r_\boldsymbol{\theta}(\mathbf{s}_t, \mathbf{a}_t)}{\partial \boldsymbol{\theta}} \right] \end{aligned}\]At optimality, the optimal discriminator for an optimal generator will always output $\frac{1}{2}$ since \(\mathcal{L}_{D^*}\) achieves the global minimum when \(p_{\texttt{data}} = p_g\): i.e. \(\exp f_\boldsymbol{\theta}^* (\mathbf{s}, \mathbf{a}) = \pi^* (\mathbf{a} \vert \mathbf{s})\). Therefore, in AIRL formulation the optimal reward approximator \(f_\boldsymbol{\theta}^*\) can recover the optimal advantage function \(A^*\):
\[f_\boldsymbol{\theta}^* (\mathbf{s}, \mathbf{a}) = \log \pi^* (\mathbf{a} \vert \mathbf{s}) = A^* (\mathbf{s}, \mathbf{a})\]Preliminary: Reward Shaping in IRL
Ng et al. ICML 1999 described a shape (class) of reward transformations that preserve the optimal policy. Specifically, for two reward functions $r$ and $\hat{r}$, they induce the same optimal policy under all transition dynamics $\mathbb{P}_\mathcal{S}$ if:
\[\hat{r} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = r (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) + \gamma \phi (\mathbf{s}^\prime) - \phi (\mathbf{s})\]for any function $\phi: \mathcal{S} \to \mathbb{R}$. Note that we have:
\[Q_{\hat{r}}^* (\mathbf{s}, \mathbf{a}) + \phi (\mathbf{s}) = \mathbb{E}_{\mathbf{s}^\prime \sim \mathbb{P}_\mathcal{S}} \left[ r (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) + \gamma \max_{ \mathbf{a}^\prime \in \mathcal{A}} \left( Q_{\hat{r}}^* (\mathbf{s}^\prime, \mathbf{a}^\prime) + \phi (\mathbf{s}^\prime) \right) \right]\]Therefore, since \(Q_{\hat{r}}^* (\mathbf{s}, \mathbf{a}) + \phi (\mathbf{s})\) satisfies the Bellman optimality equation for $r$, we obtain:
\[Q_r^* (\mathbf{s}, \mathbf{a}) = Q_{\hat{r}}^* (\mathbf{s}, \mathbf{a}) + \phi (\mathbf{s})\]This leads to the optimal policy (i.e., optimal advantange) is invariant:
\[\require{cancel} \begin{aligned} A_{r}^* (\mathbf{s}, \mathbf{a}) & = Q_{r}^* (\mathbf{s}, \mathbf{a}) - V_{r}^* (\mathbf{s}) \\ & = Q_{\hat{r}}^* (\mathbf{s}, \mathbf{a}) + \cancel{\phi (\mathbf{s})} - \max_{\mathbf{a} \in \mathcal{A}} \left\{ Q_{\hat{r}}^* (\mathbf{s}, \mathbf{a}) + \cancel{\phi (\mathbf{s})} \right\} \\ & = A_\hat{r}^* (\mathbf{s}, \mathbf{a}) \end{aligned}\]Due to such optimal policy invariance, IRL can suffer from reward ambiguity and fail to learn robust reward functions. In particular, if the IRL algorithm recovers a optimal policy invariant reward $\hat{r} (\mathbf{s}, \mathbf{a})$ under MDP $\mathcal{M}$ with transition dynamic $\mathcal{T}$ where $\phi \neq 0$, it cannot be generalized to another MDP $\mathcal{M}’$ with different dynamic $\mathcal{T}’ \neq \mathcal{T}$. For simple example, consider deterministic MDP $\mathcal{T} (\mathbf{s}, \mathbf{a}) = \mathbf{s}^\prime$ and:
\[\hat{r} (\mathbf{s}, \mathbf{a}) = r (\mathbf{s}, \mathbf{a}) + \gamma \phi (\mathcal{T} (\mathbf{s}, \mathbf{a})) - \phi (\mathbf{s})\]We can observe that $\hat{r} (\mathbf{s}, \mathbf{a})$ no longer lies in the equivalence class of shaped reward for $\mathcal{M}^\prime$, which implies the optimal policy $\pi^*$ learned from $\mathcal{M}$ is not generalizable.
Algorithm: State-centric Approximation
To address the reward ambiguity problem, AIRL employs an additional shaping term to mitigate the effects of unwanted shaping:
\[f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = g_\boldsymbol{\theta} (\mathbf{s}) + \gamma h_\boldsymbol{\phi} (\mathbf{s}^\prime) - h_\boldsymbol{\phi} (\mathbf{s})\]inducing the modified discriminator:
\[D_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = \frac{\exp f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime)}{\exp f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) + \pi (\mathbf{a} \vert \mathbf{s})}\]and the discriminator loss:
\[\mathcal{L}_{\texttt{AIRL}} (\boldsymbol{\theta}, \boldsymbol{\phi}) = - \mathbb{E}_{\pi} \left[ \sum_{t=0}^{T} \log \left( 1 - D_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}_t, \mathbf{a}_t, \mathbf{s}_{t+1}) \right) \right] - \mathbb{E}_{\mathcal{D}} \left[ \sum_{t=0}^{T} \log D_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}_t, \mathbf{a}_t, \mathbf{s}_{t+1}) \right]\]The generator (policy) $\pi$ can be optimized any RL algorithm using the following reward function $\hat{r}_{\boldsymbol{\theta}, \boldsymbol{\phi}}$ defined by the discriminator confusion:
\[\begin{aligned} \hat{r}_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) & = \log D_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) - \log \left(1 - D_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) \right) \\ & = \log \frac{\exp \left(f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime)\right)}{\exp \left(f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime)\right) + \pi (\mathbf{a} \vert \mathbf{s})} - \log \frac{\pi (\mathbf{a} \vert \mathbf{s})}{\exp \left(f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime)\right) + \pi (\mathbf{a} \vert \mathbf{s})} \\ & = f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}) - \log \pi (\mathbf{a} \vert \mathbf{s}) \end{aligned}\]

Theoretical Analysis: Recovering Rewards
The advantage of this formulation is that we can now parametrize $g_\boldsymbol{\theta} (\mathbf{s})$ as solely a function of the state. This enables us to extract rewards that are disentangled from the dynamics of the environment in which they were trained, which is essential for tasks where the dynamics model at test time differs from that at training time. Under this restricted case, we can prove that AIRL can recover state-only reward functions $r^* (\mathbf{s})$ of deterministic MDPs:
\[\begin{aligned} g_{\boldsymbol{\theta}}^* (\mathbf{s}) & = r^* (\mathbf{s}) + \mathrm{const} \\ h_{\boldsymbol{\phi}}^* (\mathbf{s}) & = V^* (\mathbf{s}) + \mathrm{const} \\ \end{aligned}\]This is consistent with the state-action formulation that the optimal reward approximator \(f_{\boldsymbol{\theta}}^*\) can recover the optimal advantage function $A^*$:
\[f_{\boldsymbol{\theta}}^* (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = \underbrace{r^* (\mathbf{s}) + \gamma V^* (\mathbf{s}^\prime)}_{Q^* (\mathbf{s}, \mathbf{a})} - V^* (\mathbf{s}) = A^* (\mathbf{s}, \mathbf{a})\]For theoretical analysis, we require a strong condition for deterministic transition dynamics called decomposability condition:
Two states $\mathbf{s}_1$, $\mathbf{s}_2$ are defined as 1-step linked under a transition dynamics $\mathcal{T}$ if $\mathbf{s}_1$ and $\mathbf{s}_2$ are reachable from the same state within one time-step: $$ \exists \mathbf{s} \in \mathcal{S}, \mathbf{a}_1, \mathbf{a}_2 \in \mathcal{A}: \; \mathcal{T} (\mathbf{s}_1 \vert \mathbf{s}, \mathbf{a}_1) > 0 \wedge \mathcal{T} (\mathbf{s}_2 \vert \mathbf{s}, \mathbf{a}_2) > 0 $$ Also, we define that this relationship can transfer through transitivity: if $\mathbf{s}_1$ and $\mathbf{s}_2$ are linked, and $\mathbf{s}_2$ and $\mathbf{s}_3$ are linked, then we also consider $\mathbf{s}_1$ and $\mathbf{s}_3$ to be linked.
A transition dynamics $\mathcal{T}$ satisfies the decomposability condition if all states $\mathbf{s} \in \mathcal{S}$ in the MDP are linked with all other states.
Now, we show that AIRL can recover a state-only reward up to a constant.
Assume that the reward network is parametrized by: $$ f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = g_\boldsymbol{\theta} (\mathbf{s}) + \gamma h_\boldsymbol{\phi} (\mathbf{s}^\prime) - h_\boldsymbol{\phi} (\mathbf{s}) $$ with $\gamma > 0$. And suppose that ground-truth reward is state-only $r (\mathbf{s})$ and the MDP has deterministic dynamics $\mathcal{T}$ satisfying the decomposability condition. Then, at optimality, we have: $$ \begin{aligned} g_{\boldsymbol{\theta}}^* (\mathbf{s}) & = r (\mathbf{s}) + k_1 \\ h_{\boldsymbol{\phi}}^* (\mathbf{s}) & = V^* (\mathbf{s}) + k_2 \\ \end{aligned} $$ for all states $\mathbf{s} \in \mathcal{S}$ with some $k_1, k_2 \in \mathbb{R}$
$\mathbf{Proof.}$
The main insight of the decomposability is that it allows us to decompose the functions state dependent $f (\mathbf{s})$ and next state dependent $g (\mathbf{s}^\prime)$ from their sum $f(\mathbf{s}) + g(\mathbf{s}^\prime)$:
$\mathbf{Proof.}$
Let $f(\mathbf{s})=a(\mathbf{s})-c(\mathbf{s})$ and $g(\mathbf{s}^\prime) = b(\mathbf{s}^\prime) - d(\mathbf{s}^\prime)$. We prove that all linked states $\mathbf{s}’$ have the same $g(\mathbf{s}’)$ by induction. Then, in a decomposable MDP, all states are linked, so $g(\mathbf{s})$ is equal to some constant $k \in \mathbb{R}$ for all $\mathbf{s} \in \mathcal{S}$. Moreover, in any (infinite-horizon) MDP, any state $\mathbf{s} \in \mathcal{S}$ must have at least one successor state $\mathbf{s}’ \in \mathcal{S}$ (possibly itself). By assumption, $f(\mathbf{s}) = g(\mathbf{s}’)$, so we prove the lemma $f(\mathbf{s}) = k$ for all $\mathbf{s} \in \mathcal{S}$.
Base case: 1-step
Since $f(\mathbf{s}) = g (\mathbf{s}^\prime)$ for any successor state $\mathbf{s}^\prime$ of $\mathbf{s}$, it must be that $g(\mathbf{s}^\prime)$ takes on the same value for all successor state $\mathbf{s}^\prime$. This shows that all 1-step linked states hae the same $g(\mathbf{s}^\prime)$.
Inductive case: $n$-step $\implies$ $(n+1)$-step
Suppose that all $n$-step linked states $\mathbf{s}’$ have the same $g(\mathbf{s}’)$. Let $\mathbf{u}$ and $\mathbf{v}$ be $(n + 1)$-step linked. That is, $\mathbf{u}$ is $n$-step linked to some intermediate $\mathbf{s} \in \mathcal{S}$ that is 1-step linked to $\mathbf{v}$ by transitivity. Therefore:
\[g(\mathbf{u}) = g(\mathbf{s}) = g(\mathbf{v})\]So in fact all $(n+1)$-step linked states $\mathbf{s}’$ have the same $g(\mathbf{s}’)$.
\[\tag*{$\blacksquare$}\]From the global minimum:
\[f_{\boldsymbol{\theta}}^* (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = A^* (\mathbf{s}, \mathbf{a}) = r (\mathbf{s}) + \gamma V^* (\mathbf{s}^\prime) - V^* (\mathbf{s})\]we have:
\[\begin{aligned} & g_{\boldsymbol{\theta}}^* (\mathbf{s}) + \gamma h_{\boldsymbol{\phi}}^* (\mathbf{s}^\prime) - h_{\boldsymbol{\phi}}^* (\mathbf{s}) = r (\mathbf{s}) + \gamma V^* (\mathbf{s}^\prime) - V^* (\mathbf{s}) \\ \Leftrightarrow & \; \left( g_{\boldsymbol{\theta}}^* (\mathbf{s}) - h_{\boldsymbol{\phi}}^* (\mathbf{s}) \right) - \left( r (\mathbf{s}) - V^* (\mathbf{s}) \right) = \gamma V^* (\mathbf{s}^\prime) - \gamma h_{\boldsymbol{\phi}}^* (\mathbf{s}^\prime) \end{aligned}\]Applying the lemma above:
\[\begin{aligned} g_{\boldsymbol{\theta}}^* (\mathbf{s}) - h_{\boldsymbol{\phi}}^* (\mathbf{s}) & = a(\mathbf{s}) = c(\mathbf{s}) + k_0 = r (\mathbf{s}) - V^* (\mathbf{s}) + k_0 \\ \gamma h_{\boldsymbol{\phi}}^* (\mathbf{s}^\prime) & = d(\mathbf{s}^\prime) = b(\mathbf{s}^\prime) + k_0 = \gamma V^* (\mathbf{s}^\prime) + k_0 \end{aligned}\]for some constant $k_0 \in \mathbb{R}$. Rearranging and using $\gamma \neq 0$:
\[\begin{aligned} g_{\boldsymbol{\theta}}^* (\mathbf{s}) & = r (\mathbf{s}) + h_{\boldsymbol{\phi}}^* (\mathbf{s}) - V^* (\mathbf{s}) + k_0 \\ h_{\boldsymbol{\phi}}^* (\mathbf{s}^\prime) & = V^* (\mathbf{s}^\prime) + \frac{k_0}{\gamma} = V^* (\mathbf{s}^\prime) + k_2 \end{aligned}\]By the decomposability condition, all states $\mathbf{s} \in \mathcal{S}$ are the successor of some state (possibly themselves). So we can substitute $\mathbf{s}^\prime$ by all $\mathbf{s} \in \mathcal{S}$:
\[h_{\boldsymbol{\phi}}^* (\mathbf{s}) = V^* (\mathbf{s}) + k_2\]Finally, by replacing terms:
\[g_{\boldsymbol{\theta}}^* (\mathbf{s}) = r (\mathbf{s}) + h_{\boldsymbol{\phi}}^* (\mathbf{s}) - V^* (\mathbf{s}) + k_0 = r (\mathbf{s}) + \underbrace{(k_0 + k_2)}_{k_1}\] \[\tag*{$\blacksquare$}\]Note that state only $g_{\boldsymbol{\theta}} (\mathbf{s})$ is important for learning a “disentangled” reward function. However, when the dynamics model remains consistent at test time, a state-action dependent $g_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a})$ performs better:
\[f_{\boldsymbol{\theta}, \boldsymbol{\phi}} (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = g_\boldsymbol{\theta} (\mathbf{s}, \mathbf{a}) + \gamma h_\boldsymbol{\phi} (\mathbf{s}^\prime) - h_\boldsymbol{\phi} (\mathbf{s})\]This implies that the practical application of AIRL may be limited as the “disentangled” reward function learned by state-only $g_{\boldsymbol{\theta}} (\mathbf{s})$ does not perform well.

Such performance gap between theory and practice may stem from several strog assumptions in the analysis. Specifically, it assumes that $f$ attains the global minimum, yet AIRL is not generally guaranteed to converge to a global optimum. Moreover, many environments have stochastic dynamics or are not 1-step linked. We also have not been able to ascertain whether the decomposability condition holds in standard RL benchmarks, such as MuJoCo tasks or Atari games.
Variational Adversarial IRL (VAIRL)
In adversarial learning methods, balancing the performance of the generator and discriminator is critical, as a discriminator with high accuracy generates relatively uninformative gradients, leading to unstable training. Peng et al. ICLR 2019 proposed a simple and general technique called variational discriminator bottleneck (VDB) that can effectively modulate the discriminator’s accuracy, thereby ensuring useful and informative gradients.
Variational Discriminator Bottleneck (VDB)
The standard MLE is prone to overfitting, and often exploit abnormalities in the data. To encourage the model to focus only on the most discriminative features, we can regularize the model using an information bottleneck:
\[\mathcal{J}(p, E) = \begin{array}[t]{cl} \underset{p, E}{\min} & \mathbb{E}_{\mathbf{x}, \mathbf{y} \sim p_{\texttt{data}}} \left[ \mathbb{E}_{\mathbf{z} \sim E(\mathbf{z} \vert \mathbf{x})} \left[ -\log p(\mathbf{y} \vert \mathbf{z}) \right] \right] \\ \textrm{ s.t. } & \mathbb{I}(X, Z) \leq I_c \end{array}\]where $E (\mathbf{z} \vert \mathbf{z})$ is an encoder that maps the features $\mathbf{x}$ to a latent distribution over $Z$, and $\mathbb{I}$ is the mutual information defined as:
\[\mathbb{I} (X, Z) = \mathbb{E} \left[ \log \frac{p(X, Z)}{p(X) p(Z)} \right] = \int p_\texttt{data}(\mathbf{x}) E (\mathbf{z} \vert \mathbf{x}) \log \frac{E(\mathbf{z} \vert \mathbf{x})}{p (\mathbf{z})} \; d\mathbf{x} \; d\mathbf{z}\]To avoid computing the intractable marginal distribution $p(\mathbf{z})$, we can incorporate variation lower bound using an approximation $q (\mathbf{z})$ of the marginal:
\[\mathbb{I} (X, Z) \leq \int p_\texttt{data}(\mathbf{x}) E (\mathbf{z} \vert \mathbf{x}) \log \frac{E(\mathbf{z} \vert \mathbf{x})}{q (\mathbf{z})} \; d\mathbf{x} \; d\mathbf{z} = \mathbb{E}_{\mathbf{x} \sim p_\texttt{data}} \left[ \mathrm{KL} (E (\mathbf{z} \vert \mathbf{x}) \Vert q (\mathbf{z})) \right]\]where the inequality is obtained from $\mathrm{KL}(p (\mathbf{z}) \Vert q(\mathbf{z}))$. This leads to an upper bound $\bar{\mathcal{J}}$ on the regularized MLE:
\[\bar{\mathcal{J}}(p, E) = \begin{array}[t]{cl} \underset{p, E}{\min} & \mathbb{E}_{\mathbf{x}, \mathbf{y} \sim p_{\texttt{data}}} \left[ \mathbb{E}_{\mathbf{z} \sim E(\mathbf{z} \vert \mathbf{x})} \left[ -\log p(\mathbf{y} \vert \mathbf{z}) \right] \right] \\ \textrm{ s.t. } & \mathbb{E}_{\mathbf{x} \sim p_\texttt{data}} \left[ \mathrm{KL} (E (\mathbf{z} \vert \mathbf{x}) \Vert q (\mathbf{z})) \right] \leq I_c \end{array}\]Incorporating this variational information bottleneck to GAN, the regularized objective $\mathcal{J}(D, E)$ for the discriminator $D$ is given by:
\[\mathcal{J}(D, E) = \begin{array}[t]{cl} \underset{D, E}{\min} & \mathbb{E}_{\mathbf{x} \sim p_{\texttt{data}}} \left[ \mathbb{E}_{\mathbf{z} \sim E(\mathbf{z} \vert \mathbf{x})} \left[ - \log D (\mathbf{z}) \right] \right] + \mathbb{E}_{\mathbf{x} \sim G} \left[ \mathbb{E}_{\mathbf{z} \sim E(\mathbf{z} \vert \mathbf{x})} \left[ - \log (1 - D(\mathbf{z})) \right] \right] \\ \textrm{ s.t. } & \mathbb{E}_{\mathbf{x} \sim \mu} \left[ \mathrm{KL} (E (\mathbf{z} \vert \mathbf{x}) \Vert q (\mathbf{z})) \right] \leq I_c \end{array}\]where $q(\mathbf{z}) = \mathcal{N}(\mathbf{0}, \mathbf{I})$ is the prior distribution, the encoder \(E(\mathbf{z} \vert \mathbf{x}) = \mathcal{N} ( \mu_\boldsymbol{\phi} (\mathbf{x}), \Sigma_\boldsymbol{\phi}( \mathbf{x}))\) models the latent distribution, and \(\mu = \frac{1}{2} p_\texttt{data} + \frac{1}{2} G\) is a mixture of the data (target) distribution and the generator. And such regularizer is named variational discriminator bottleneck (VDB).
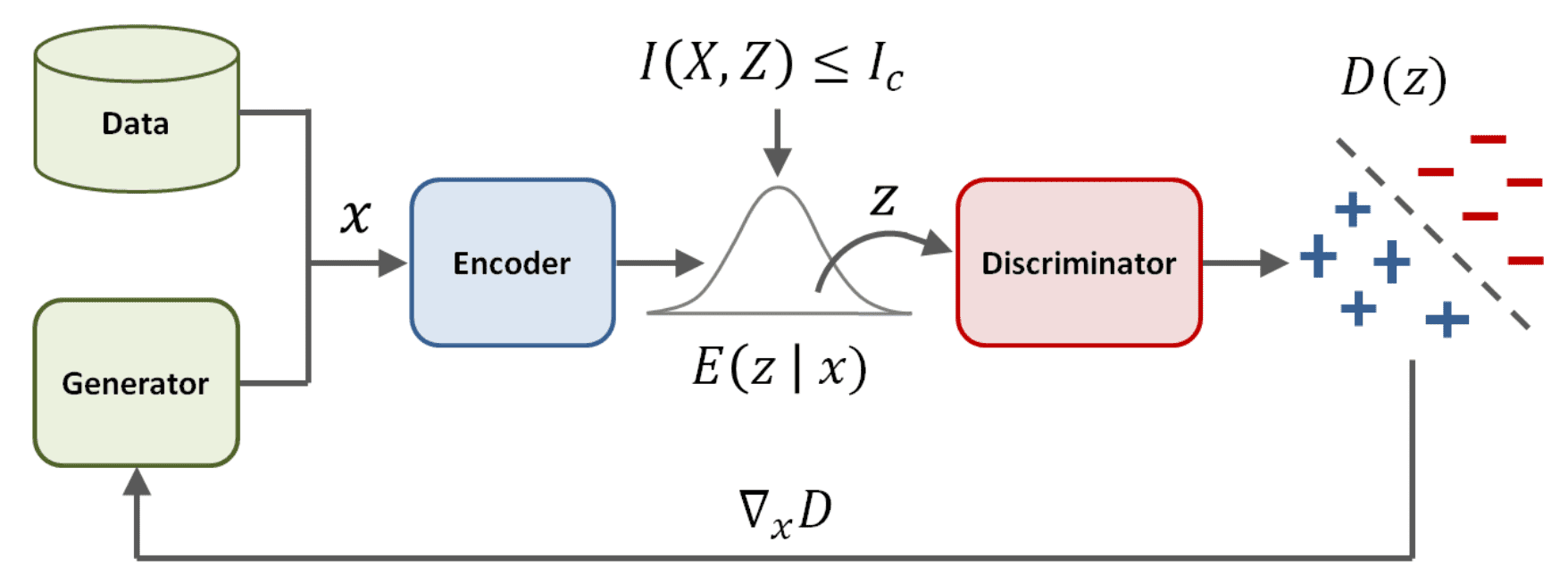
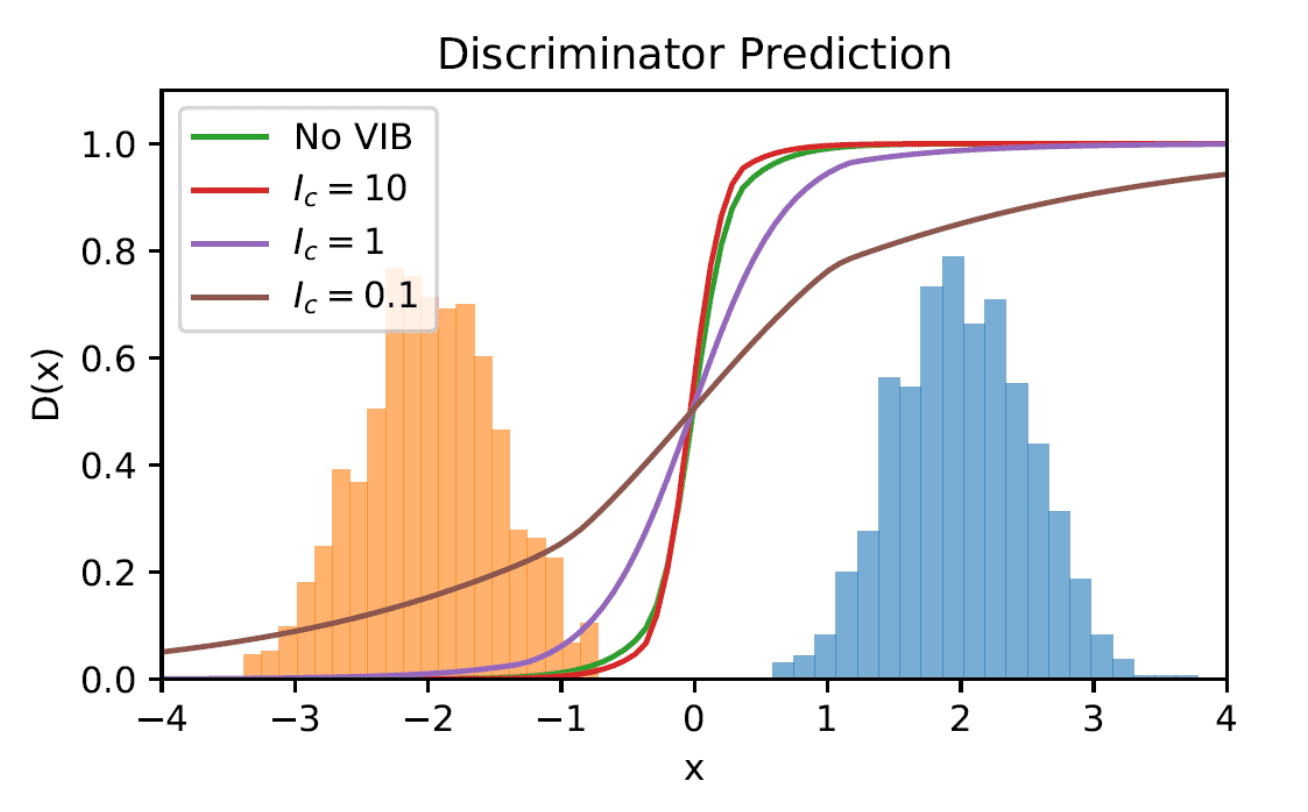
As the optimal discriminator in an adversarial learning framework can perfectly classify all samples, its gradients become zero almost everywhere. Consequently, as the discriminator approaches this optimum, the gradients for the generator diminish accordingly. However, with VDB, by restricting the information flow $I_c < 1$, where $1 \textrm{bit}$ is the minimum amount of information required for binary classification, the discriminator is prevented from perfectly distinguishing between the distributions.
The following figure visualizes the decision boundaries learned with different bounds $I_c$. Without a VDB, the discriminator learns a sharp decision boundary, resulting in vanishing gradients across much of the space. However, as $I_c$ decreases, the decision boundary becomes smoother, providing more informative gradients that the generator can effectively leverage.
Algorithm: AIRL with VDB
To apply VDB regularizer into AIRL framework, the stochastic encoders $E_g (\mathbf{z}_g \vert \mathbf{s})$, $E_h(\mathbf{z}_h \vert \mathbf{s})$ are introduced to the discriminator and $g(\mathbf{s}, \mathbf{a})$, $h(\mathbf{s})$ are modified to be functions $D_g (\mathbf{z}_g)$, $D_h (\mathbf{z}_h)$ of these encodings:
\[\begin{aligned} \texttt{AIRL: } & \begin{aligned}[t] & D (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = \frac{\exp \left( f(\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) \right)}{\exp \left( f(\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) \right) + \pi (\mathbf{a} \vert \mathbf{s})} \\ & \text{ where } f (\mathbf{s}, \mathbf{a}, \mathbf{s}^\prime) = g(\mathbf{s}, \mathbf{a}) + \gamma h (\mathbf{s}^\prime) - h (\mathbf{s}) \end{aligned} \\ \texttt{VAIRL: } & \begin{aligned}[t] & D (\mathbf{s}, \mathbf{a}, \mathbf{z}) = \frac{\exp \left( f(\mathbf{z}_g, \mathbf{z}_h, \mathbf{z}_h^\prime) \right)}{\exp \left( f(\mathbf{z}_g, \mathbf{z}_h, \mathbf{z}_h^\prime) \right) + \pi (\mathbf{a} \vert \mathbf{s})} \\ & \text{ where } f (\mathbf{z}_g, \mathbf{z}_h, \mathbf{z}_h^\prime) = D_g(\mathbf{z}_g) + \gamma D_h (\mathbf{z}_h^\prime) - D_h (\mathbf{z}_h) \end{aligned} \end{aligned}\]with a modified objective:
\[\begin{aligned} \mathcal{L}_\texttt{VAIRL} (D,E) = \underset{D,E}{\min} \ \underset{\beta \geq 0}{\max} \ & \mathbb{E}_{\mathbf{s}, \mathbf{s}' \sim p_\mathcal{D} (\mathbf{s}, \mathbf{s}')} \left[\mathbb E_{\mathbf{z} \sim E(\mathbf{z} \vert \mathbf{s}, \mathbf{s}')} \left[-\mathrm{log} D(\mathbf{s}, \mathbf{a}, \mathbf{z}) \right]\right] \\ & + \mathbb E_{\mathbf{s}, \mathbf{s}' \sim \pi(\mathbf{s}, \mathbf{s}')} \left[\mathbb E_{\mathbf{z} \sim E(\mathbf{z} \vert \mathbf{s}, \mathbf{s}')} \left[-\mathrm{log} \left(1 - D(\mathbf{s}, \mathbf{a}, \mathbf{z})\right) \right]\right] \\ & + \beta \left(\mathbb{E}_{\mathbf{s}, \mathbf{s}' \sim \tilde{\pi}(\mathbf{s}, \mathbf{s}')}\left[\mathrm{KL}\left(E(\mathbf{z} \vert \mathbf{s}, \mathbf{s}') \middle\Vert q(\mathbf{z}) \right) \right] - I_c \right) \end{aligned}\]where $\pi (\mathbf{s}, \mathbf{s}’)$ denotes the joint distribution of successive states from a policy, $\tilde{\pi} = \frac{1}{2} p_\mathcal{D} + \frac{1}{2} \pi$ and \(E (\mathbf{z} \vert \mathbf{s}, \mathbf{s}') = E_g (\mathbf{z}_g \vert \mathbf{s}) \cdot E_h (\mathbf{z}_h \vert \mathbf{s}) \cdot E_h (\mathbf{z}_h^\prime \vert \mathbf{s}^\prime)\).
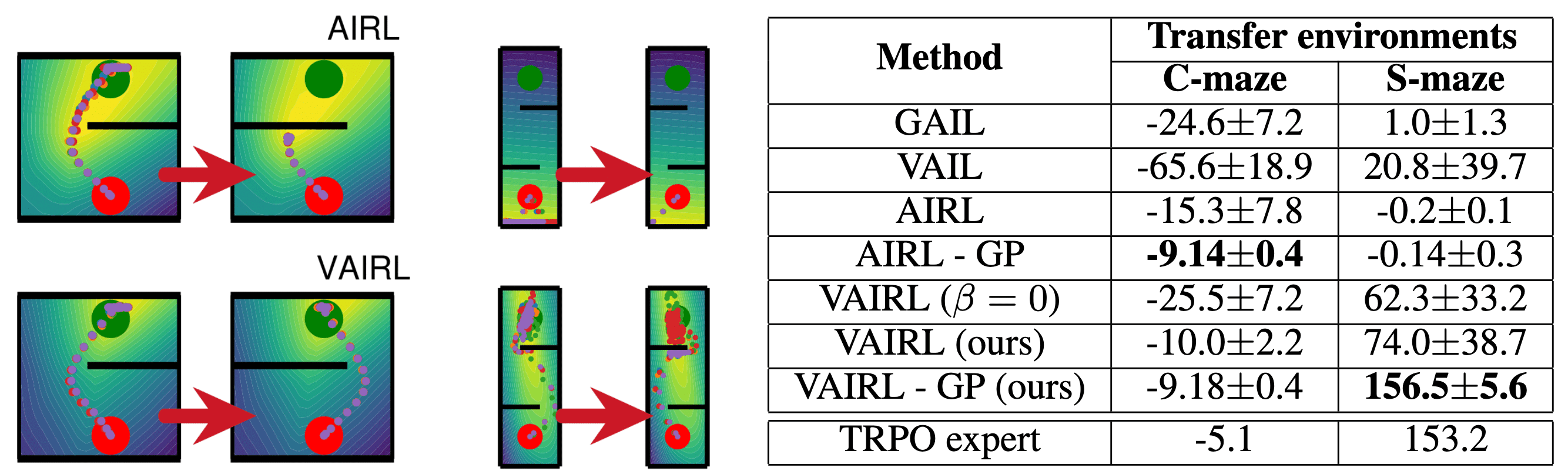
Experimentally, in the C-maze and S-maze environments, AIRL learns a reward function that overfits to the training task, as evidenced by the reward visualization and the higher return variance. This reward function also fails to transfer effectively to the mirrored maze on the right. In contrast, VAIRL learns a smoother reward function which enables more reliable transfer to the new environment.
$f$-divergence Max-Ent IRL ($f$-MAX)
Adversarial approaches to Max-Ent IRL can be further generalized through the perspective of divergence minimization.
Preliminary: $f$-divergence & $f$-GAN
Probabilistic divergences, such as the well-known Kullback-Leibler (KL) divergence, quantify the difference between two given probability distributions. And a broad class of such divergences is known as $f$-divergences:
\[D_f (p \Vert q) = \int_\mathcal{X} q(x) f\left( \frac{p(x)}{q(x)} \right)\]for a convex function $f:[0, \infty) \to (-\infty, \infty]$ such that
- $f(x)$ is finite for all $x > 0$
- $f(0) = \lim_{t \to 0^{+}} f(t)$ (which could be infinite)
- $f(1) = 0$ to make $D_f (p \Vert p) = 0$
We call $f$ the generator of $D_f$. Different choices of $f$ recover popular divergences as special cases:
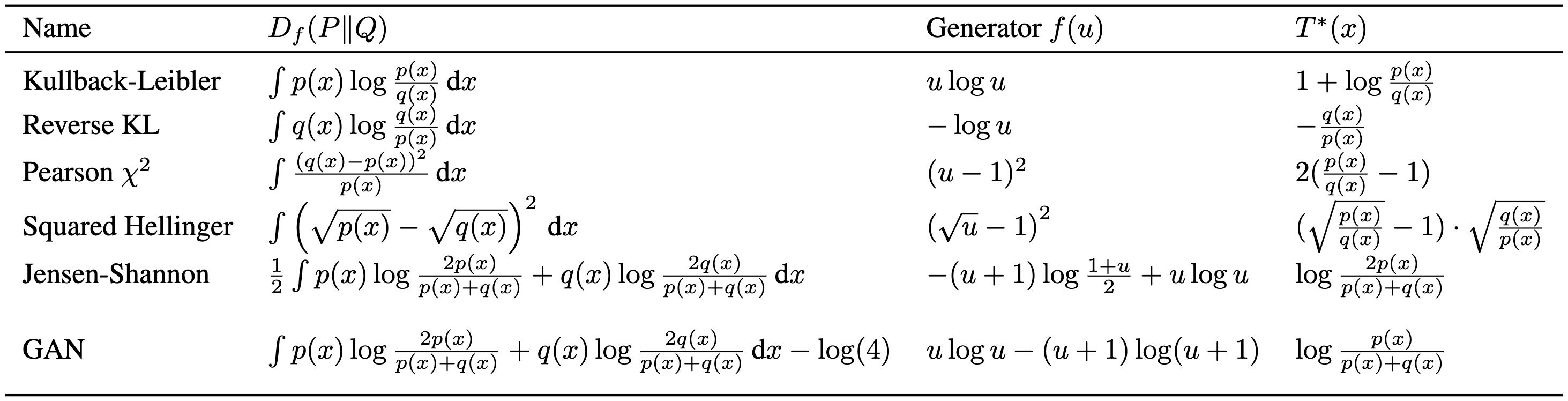
Variational Representation
To estimate $f$-divergences using only samples from distributions $p$ and $q$, we can compute a variational representation of the divergence. First, we define convex conjugate $f^*$ of convex function $f$:
\[f^* (y) = \sup_{x \in \mathrm{dom}(f)} \left\{ xy - f(x) \right\}\]This is convex again, and the pair $(f, f^*)$ is dual to another in the sense that $f^{**} = f$. Therefore:
\[f(x) = \sup_{y \in \mathrm{dom}(f^*)} \left\{ yx - f^*(y) \right\}\]Then we obtain:
\[\begin{aligned} D_f (p \Vert q) & = \int_\mathcal{X} q (x) \sup_{y \in \mathrm{dom}(f^*)} \left( y \frac{p(x)}{q(x)} - f^* (y) \right) \; \mathrm{d}x \\ & \geq \sup_{T \in \mathcal{T}} \left( \int_\mathcal{X} p(x) T(x) \mathrm{d}x - \int_\mathcal{X} q(x) f^* (T(x)) \mathrm{d} x \right) \\ & = \sup_{T \in \mathcal{T}} \left( \mathbb{E}_{x \sim p} \left[ T(x) \right] - \mathbb{E}_{x \sim q} \left[ f^* (T(x)) \right] \right) \end{aligned}\]where $\mathcal{T}$ is an arbitrary class of functions $T: \mathcal{X} \to \mathbb{R}$. Note that this lower bound is tight if and only if $\frac{p(x)}{q(x)} \in \partial f^* (T(x))$ for all $x \in \mathcal{X}$ where $\partial \phi (t)$ is subdifferential:
\[\partial \phi (t) = \{ z \in \mathbb{R} \vert \phi (y) \geq \phi (t) + z (y - t) \}\]As a special case, if $\phi$ is differentiable at $t$, then \(\partial \phi (t) = \{ \phi'(t)\}\). Then, if $\frac{p(x)}{q(x)} \in \partial f^* (T(x))$, for all $y \in \mathbb{R}$:
\[\begin{aligned} & \; \int_\mathcal{X} \left( y \cdot p(x) - f^* (y) q(x) \right) \; \mathrm{d}x \leq \int_\mathcal{X} \left( p(x) T (x) - q(x) f^* (T(x)) \right) \mathrm{d} x \\ \implies & \; \begin{aligned}[t] \int_\mathcal{X} \sup_{y \in \mathrm{dom} (f^*)} \left( y \cdot p(x) - f^* (y) q(x) \right) & \leq \int_\mathcal{X} \left( p(x) T (x) - q(x) f^* (T(x)) \right) \mathrm{d} x \\ & \leq \sup_{T \in \mathcal{T}} \left( \int_\mathcal{X} \left( p(x) T (x) - q(x) f^* (T(x)) \right) \mathrm{d} x \right) \end{aligned} \end{aligned}\]By convex duality, this is true if $T^* (x) \in \partial f (p(x) / q(x))$ for all $x \in \mathcal{X}$. If $f$ is differentiable, this condition is equivalent to:
\[T(x) = f^\prime \left( \frac{p(x)}{q(x)} \right)\]$f$-GAN
Applying the above discussion to the generative-adversarial framework, $f$-GAN, proposed by Nowozin et al. 2016, leverages the following minimax optimization:
\[\min_G \max_D \mathbb{E}_{\mathbf{x} \sim p_\texttt{data}} \left[ D (\mathbf{x}) \right] - \mathbb{E}_{\mathbf{x} \sim G} \left[ f^* (D(\mathbf{x}))\right]\]Algorithm: IRL by $f$-divergence minimization
Using the $f$-GAN formulation, the AIRL objective can be generalized as:
\[\min_\pi \max_{D} \; \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim p_\texttt{data}} \left[ D (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim \pi} \left[ f^* (D (\mathbf{s}, \mathbf{a})) \right]\]The inner maximization optimizes the discriminator $D$ so that the maximand best approximates $D_f ( \rho^\texttt{data} (\mathbf{s}, \mathbf{a}) \vert \rho^\pi (\mathbf{s}, \mathbf{a}))$. To optimize this objective, $f$-MAX repeats the following iterative optimization procedure:
\[\begin{aligned} & \mathbf{(1): } \max_{D} \; \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim p_\texttt{data}} \left[ D (\mathbf{s}, \mathbf{a}) \right] - \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim \pi} \left[ f^* (D (\mathbf{s}, \mathbf{a})) \right] \\ & \mathbf{(2): } \max_\pi \; \mathbb{E}_\pi \left[ \sum_{t=0}^\infty f^* (D(\mathbf{s}_t, \mathbf{a}_t)) \right] \\ \end{aligned}\]Forward Adversarial IRL (FAIRL)
While $f$-MAX is a general algorithm applicable to most choices of $f$, it cannot be used for the specific case of forward KL, i.e., $\mathrm{KL} (\rho^\texttt{data} (\mathbf{s}, \mathbf{a}) \Vert \rho^\pi (\mathbf{s}, \mathbf{a}))$. To address this, the authors of $f$-MAX also introduced a separate method called forward AIRL (FAIRL) that optimizes this divergence.
Problem: Forward KL
If $D^*$ denotes the maximizer of $f$-MAX for a given policy $\pi$, the following setups are required to implement the forward KL with $f$-divergence:
\[\begin{array}{ll} u := \frac{\rho^{\texttt{data}}(\mathbf{s}, \mathbf{a})}{\rho^\pi(\mathbf{s}, \mathbf{a})} & f(u):=u \log u \\ f^* (t) = \exp (t-1) & D^* = 1 + \log \frac{\rho^{\texttt{data}}(\mathbf{s}, \mathbf{a})}{\rho^\pi(\mathbf{s}, \mathbf{a})} \end{array}\]Then, the objective for the policy under the optimal $D^*$ becomes:
\[\begin{aligned} \max_\pi \; \mathbb{E}_{\pi} \left[ \sum_{t=0}^\infty f^* (D^* (\mathbf{s}_t, \mathbf{a}_t)) \right] & \propto \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim \rho^\pi} \left[ f^* (D^* (\mathbf{s}, \mathbf{a})) \right] \\ & = \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim \rho^\pi} \left[ \exp \left( \left( 1 + \log \frac{\rho^{\texttt{data}}(\mathbf{s}, \mathbf{a})}{\rho^\pi(\mathbf{s}, \mathbf{a})} \right) - 1 \right) \right] \\ & = \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim \rho^\pi} \left[ \frac{\rho^{\texttt{data}}(\mathbf{s}, \mathbf{a})}{\rho^\pi(\mathbf{s}, \mathbf{a})} \right] \\ & = 1 \end{aligned}\]Hence, there is no signal to train the policy $\pi$ when $D_f$ is forward KL.
Algorithm: Forward KL version of AIRL
To implement forward KL, FAIRL defines the reward for the policy to be:
\[\begin{gathered} r(\mathbf{s}, \mathbf{a}) := \exp (h (\mathbf{s}, \mathbf{a})) \cdot (-h (\mathbf{s}, \mathbf{a})) \\ \text{ where } h (\mathbf{s}, \mathbf{a}) := \log D (\mathbf{s}, \mathbf{a}) - \log (1 - D (\mathbf{s}, \mathbf{a})) \end{gathered}\]Then the generator (policy) is optimized to maximize \(\mathbb{E}_\pi [\sum_{t=0}^\infty r(\mathbf{s}_t, \mathbf{a}_t)]\). Assuming the discriminator $D$ is optimal:
\[D (\mathbf{s}, \mathbf{a}) = \frac{\rho^\texttt{data} (\mathbf{s}, \mathbf{a})}{\rho^\texttt{data} (\mathbf{s}, \mathbf{a}) + \rho^\pi (\mathbf{s}, \mathbf{a})}\]we can show that this return is equivalent to the forward KL:
\[\begin{aligned} \mathbb{E}_\pi \left[ r (\mathbf{s}_t, \mathbf{a}_t) \right] & = \mathbb{E}_\pi \left[ \sum_{t=0}^\infty \exp (h (\mathbf{s}_t, \mathbf{a}_t)) \cdot (- h (\mathbf{s}_t, \mathbf{a}_t)) \right] \\ & = \mathbb{E}_\pi \left[ \sum_{t=0}^\infty \frac{\rho^\texttt{data} (\mathbf{s}_t, \mathbf{a}_t)}{\rho^\pi (\mathbf{s}_t, \mathbf{a}_t)} \cdot \log \frac{\rho^\pi (\mathbf{s}_t, \mathbf{a}_t)}{\rho^\texttt{data} (\mathbf{s}_t, \mathbf{a}_t)} \right] \\ & \propto \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim \rho^\pi} \left[ \frac{\rho^\texttt{data} (\mathbf{s}, \mathbf{a})}{\rho^\pi (\mathbf{s}, \mathbf{a})} \cdot \log \frac{\rho^\pi (\mathbf{s}, \mathbf{a})}{\rho^\texttt{data} (\mathbf{s}, \mathbf{a})} \right] \\ & = \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim \rho^\texttt{data}} \left[ \log \frac{\rho^\pi (\mathbf{s}, \mathbf{a})}{\rho^\texttt{data} (\mathbf{s}, \mathbf{a})} \right] \\ & = - \mathrm{KL} (\rho^\texttt{data} (\mathbf{s}, \mathbf{a}) \Vert \rho^\pi (\mathbf{s}, \mathbf{a})) \end{aligned}\]Therefore, FAIRL converts the AIRL algorithm into its forward KL counterpart by simply modifying the reward function used.
References
[1] Finn et al. “A Connection between Generative Adversarial Networks, Inverse Reinforcement Learning, and Energy-Based Models”, NIPS 2016 Workshop on Adversarial Training
[2] Finn et al. “Guided Cost Learning: Deep Inverse Optimal Control via Policy Optimization”, ICML 2016
[3] Ho et al. “Generative Adversarial Imitation Learning”, NIPS 2016
[4] Fu et al. “Learning Robust Rewards with Adversarial Inverse Reinforcement Learning”, ICLR 2018
[5] Peng et al. “Variational Discriminator Bottleneck: Improving Imitation Learning, Inverse RL, and GANs by Constraining Information Flow”, ICLR 2019
[6] Ghasemipour et al. “A Divergence Minimization Perspective on Imitation Learning Methods”, CoRL 2019
[7] Nowozin et al. “f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization”, NIPS 2016
[8] Wikipedia, f-divergence
[9] Nguyen et al. “Estimating divergence functionals and the likelihood ratio by convex risk minimization”, arXiv:0809.0853
[10] Convex Optimization – Boyd and Vandenberghe
[11] Gleave et al. “A Primer on Maximum Causal Entropy Inverse Reinforcement Learning”, arXiv:2203.11409

Leave a comment