[RL] Data-Augmented Visual RL

In computer vision, supervised learning has tackled data efficiency and generalization by incorporating useful priors, with data augmentation being a particularly impactful one. Critical to the early success of CNNs, data augmentation has recently bolstered supervised, semi-supervised, and self-supervised learning by forcing CNNs to learn consistencies across multiple augmented views of the same data point, resulting in visual representations that improve generalization, data efficiency, and transfer learning.

Inspired by these advances, data-augmented visual reinforcement learning methods, exemplified by RAD, DrQ, and its enhanced version DrQv2, have been instrumental in enabling robust learning from pixel data, effectively bridging the performance gap between state-based and image-based RL.

Reinforcement Learning with Augmented Data (RAD)

Reinforcement Learning with Augmented Data (RAD), introduced by Laskin et al. NeurIPS 2020, is the first approach to leverage data augmentations directly in reinforcement learning without any auxiliary loss. The authors explored the effectiveness of data augmentations in model-free RL for both off-policy (SAC) and on-policy (PPO) settings by applying stochastic augmentations to image observations before feeding them to the agent during training.

$\mathbf{Fig\ 1.}$ Reinforcement Learning with Augmented Data (Laskin et al. 2020)

In DMControl experiments, the authors assessed data efficiency by evaluating RAD’s performance at 100k steps (low-sample regime) and 500k steps (asymptotically optimal regime) of environment interactions during training. As a result, RAD enhances pixel SAC’s performance by 4x on both DMControl100k and DMControl500k datasets, achieving these gains purely through data augmentation, without incorporating forward model learning or any auxiliary tasks.

$\mathbf{Fig\ 2.}$ Scores for RAD and baseline methods on DMControl100k and DMControl500k (Laskin et al. 2020)

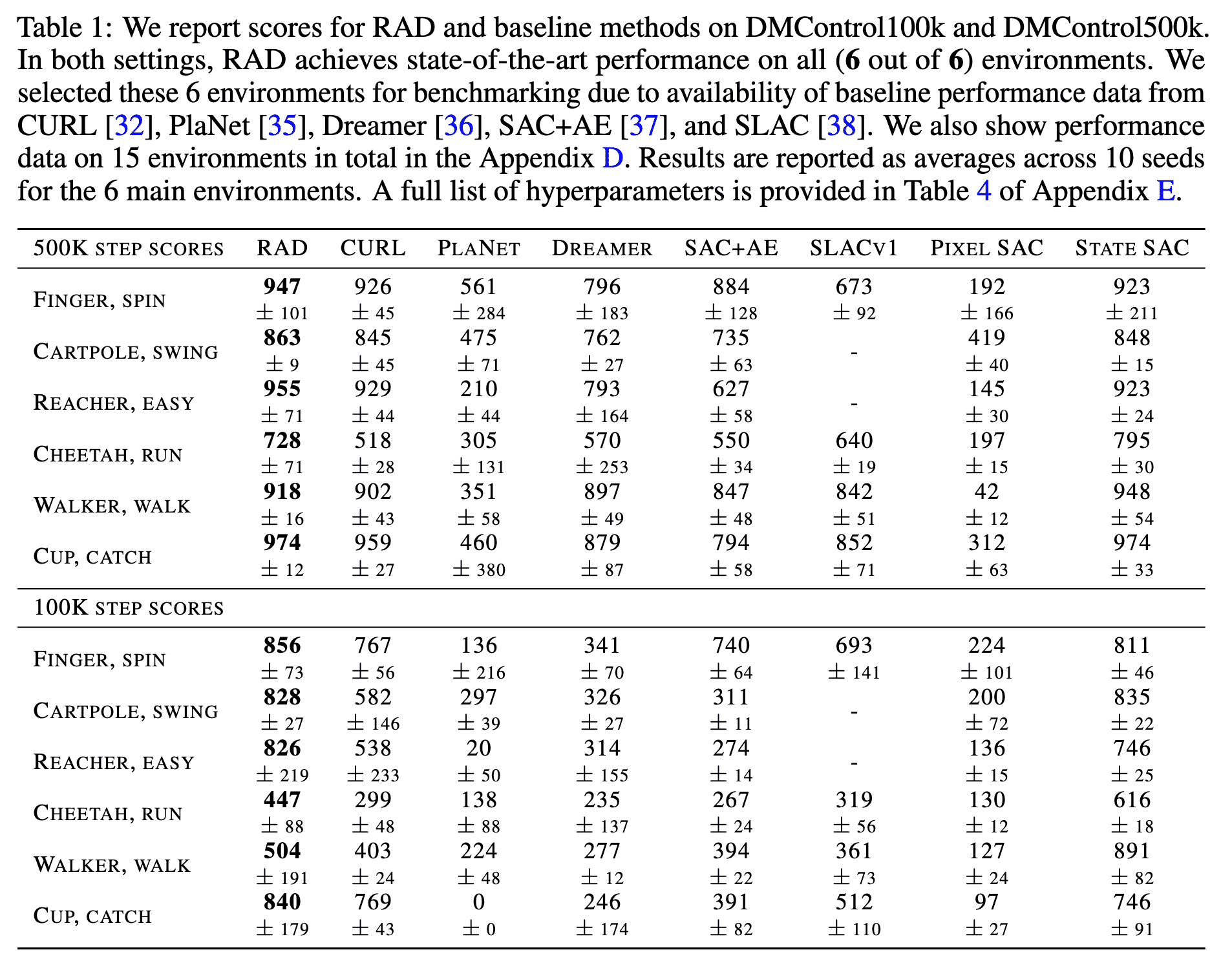
To identify the most effective augmentations, the authors ran RAD with combinations of two sequential data augmentations (e.g., crop followed by grayscale) on the Walker Walk DMC environment, reporting scores at 500k environment steps. This environment was chosen because SAC without augmentation performs poorly. Their ablations reveal that most augmentations enhance the base policy’s performance, with random crop proving the most effective by a significant margin.

Additionally, a spatial attention map from the output of the final convolutional layer shows that, without augmentation, the activation is concentrated mainly on the forward knee. In contrast, with random crop/translate, the activation covers the body’s entire edge, offering a more comprehensive and resilient representation of the state. The quality of the attention map with random crop indicates that RAD enhances the agent’s contingency-awareness—its ability to recognize controllable aspects of the environment—thereby boosting data efficiency.

$\mathbf{Fig\ 3.}$ Ablation Studies (Laskin et al. 2020)

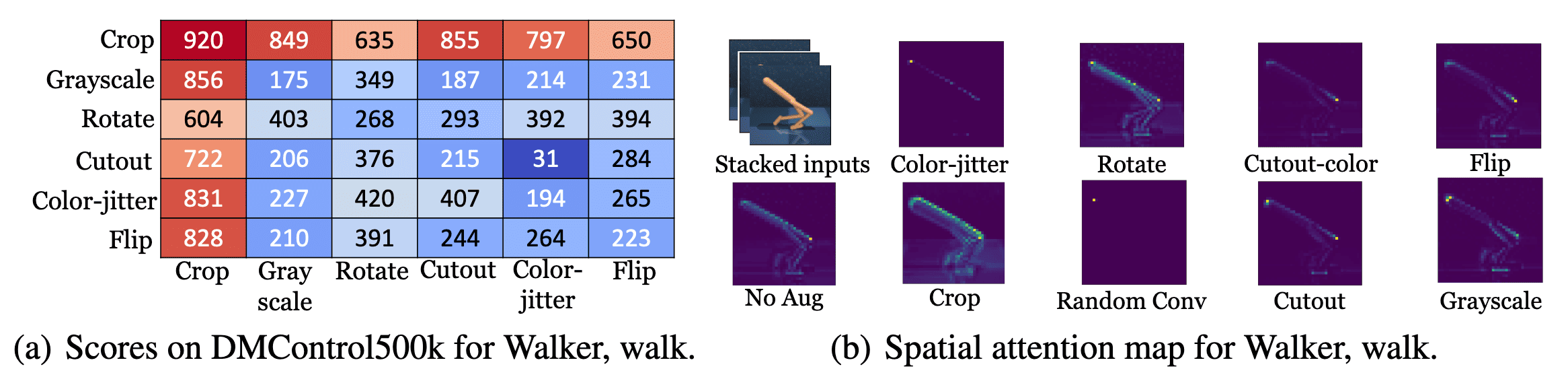
To analyze the effects of random crop, the authors decomposed it into its two sub-augmentations: (a) random window, which masks a random boundary region of the image at the locations where crop would remove it, and (b) random translation, where the full image is placed within a larger, zero-padded frame and then randomly shifted within this frame (e.g., translating a $100 \times 100$ pixel image within a $108 \times 108$ frame).

The learning curves from each augmentation reveal that translations provide a clear performance benefit, whereas the random masking effect of windowing has minimal impact. Interestingly, random crop—combining both windowing and translation—sometimes reduced variance in learning outcomes.

$\mathbf{Fig\ 4.}$ Analyzing Random Crop (Laskin et al. 2020)

Data-Regularized Q (DrQ)

Concurrently and independently with RAD, Kostrikov et al. NeurIPS 2020 proposed Data-Regularized Q that utilized random cropping and regularized Q-functions in conjunction with the off-policy RL algorithm SAC.

Regularizing the value function with data augmentation

Let $f : \mathcal{S} \times \mathcal{T} \to \mathcal{S}$ be an optimality invariant state transformation which is a mapping that preserves the $Q$-values:

\[\forall \mathbf{s}, \mathbf{a} \in \mathcal{S} \times \mathcal{A} \text{ and } \phi \in \mathcal{T}: \; Q(\mathbf{s}, \mathbf{a}) = Q(f(\mathbf{s}, \phi), \mathbf{a})\]

where $\phi$ are the parameters of $f$. For example, $f$ can be a random image translations with the random amount of translation $\phi$. For every state $\mathbf{s} \in \mathcal{S}$, DrQ utilized this transformations $f$ by generating of several surrogate states with the same $Q$-values, thus providing a mechanism to reduce the variance of $Q$-function estimation. Specifically, for an arbitrary state distribution $\mu$ and policy $\pi$, instead of using a single sample Monte-Carlo estimation $Q (\mathbf{s}, \mathbf{a})$ of the following expectation:

\[\mathbb{E}_{\mathbf{s} \sim \mu(\cdot), \mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} [ Q(\mathbf{s}, \mathbf{a} )] \approx Q (\mathbf{s}, \mathbf{a})\]

we can generate $K$ samples through random transformations and obtain an estimate with lover variance:

\[\mathbb{E}_{\mathbf{s} \sim \mu(\cdot), \mathbf{a} \sim \pi (\cdot \vert \mathbf{s})} [ Q(\mathbf{s}, \mathbf{a} )] \approx \frac{1}{K} \sum_{k=1}^K Q (f(\mathbf{s}, \phi_k), \mathbf{a}_k)\]

where $\phi_k \sim \mathcal{T}$ and \(\mathbf{a}_k \sim \pi (\cdot \vert f(\mathbf{s}, \phi_k))\).

Data-regularized Q (DrQ)

Data-regularized Q regularizes the online $Q_\theta$ and target $Q_{\theta^\prime}$ using different set of augmentations \(\{ f (\mathbf{s}_n, \phi_{n, m}) \}_{n=1, m=1}^{N, M}\) and \(\{ f (\mathbf{s}_n^\prime, \phi_{n, k}^\prime) \}_{n=1, k=1}^{N, K}\) to each functions, for every transition tuple \(\{ (\mathbf{s}_n, \mathbf{a}_n, r_n, \mathbf{s}_n^\prime ) \sim \mathcal{D} \}_{n=1}^N\):

\[\theta \leftarrow \theta - \lambda \cdot \nabla_\theta \frac{1}{N \times M} \sum_{n=1, m=1}^{N, M} \left( Q_\theta (f (\mathbf{s}_n, \phi_{n, m} ), \mathbf{a}_n) - y_n \right)^2 \\ \text{ where } y_n = r_n + \gamma \cdot \frac{1}{K} \sum_{k=1}^K Q_{\theta^\prime} (f(\mathbf{s}_{n}^\prime, \phi_{n, k}^\prime), \mathbf{a}_{n, k}^\prime) \text{ and } \mathbf{a}_{n, k}^\prime \sim \pi (\cdot \vert f (\mathbf{s}_n^\prime, \phi_{n, k}^\prime))\]

Note that DrQ with $K = 1, M = 1$ exactly recovers the concurrent work of RAD. The following pseudocode details how they are incorporated into a generic pixel-based off-policy actor-critic algorithm.

$\mathbf{Fig\ 5.}$ Data-regularized Q applied to off-policy Actor-Critic (Kostrikov et al. 2020)

In practice, $K = 2$ and $M = 2$ work best, when image shifts are selected as the class of image transformations $f$, with $\phi = \pm 4$ as explained in the next sub-section.

$\mathbf{Fig\ 6.}$ Performance comparisons of different $(K, M)$ values (Kostrikov et al. 2020)

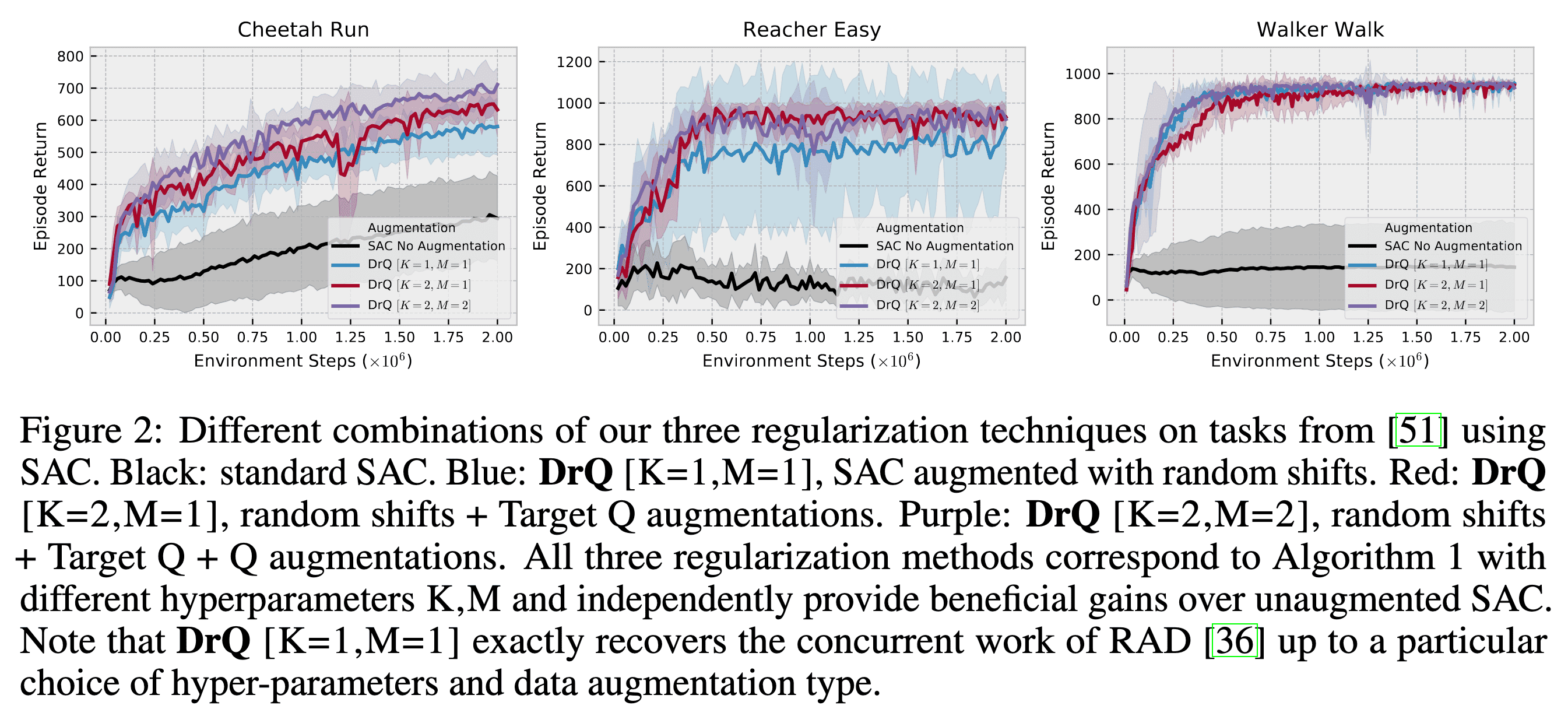
Experimental Results

For DrQ, the authors evaluated popular image augmentation techniques, including random shifts, cutouts, vertical and horizontal flips, random rotations, and intensity jittering. Similar to RAD, they found that random shifts exhibit an effective balance of simplicity and performance.

$\mathbf{Fig\ 7.}$ Various image augmentations have different effect on the agent’s performance (Kostrikov et al. 2020)

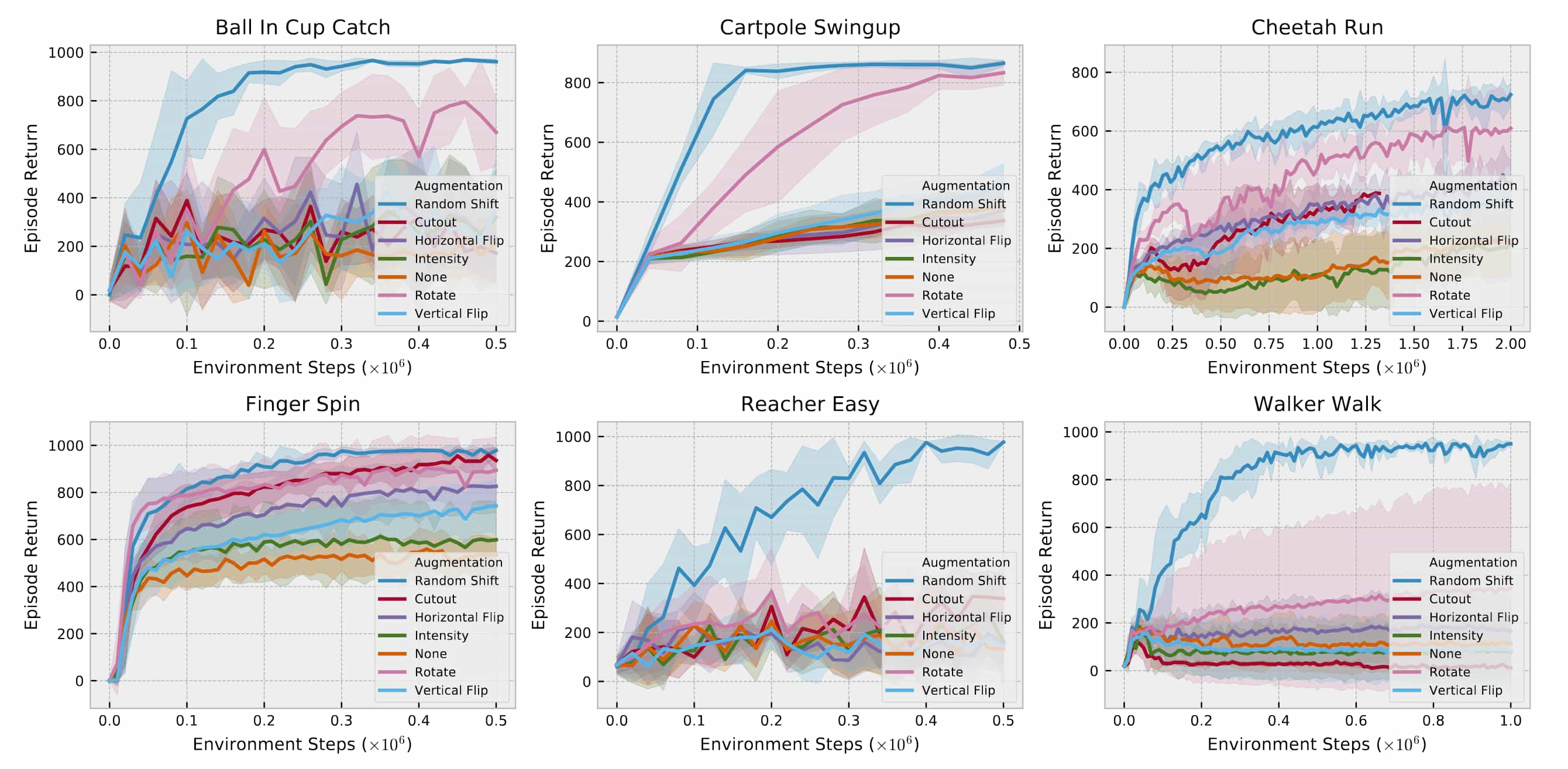
The following learning curves illustrate the impact of random shifts applied during SAC training on several image-based DMC environments, where the observation images are given by $84 \times 84$. The images are padded by $4$ pixels on each side, followed by a random $84 \times 84$ crop that results in the original image shifted by $\pm 4$ pixels. This procedure is repeated each time an image is sampled from the replay buffer.

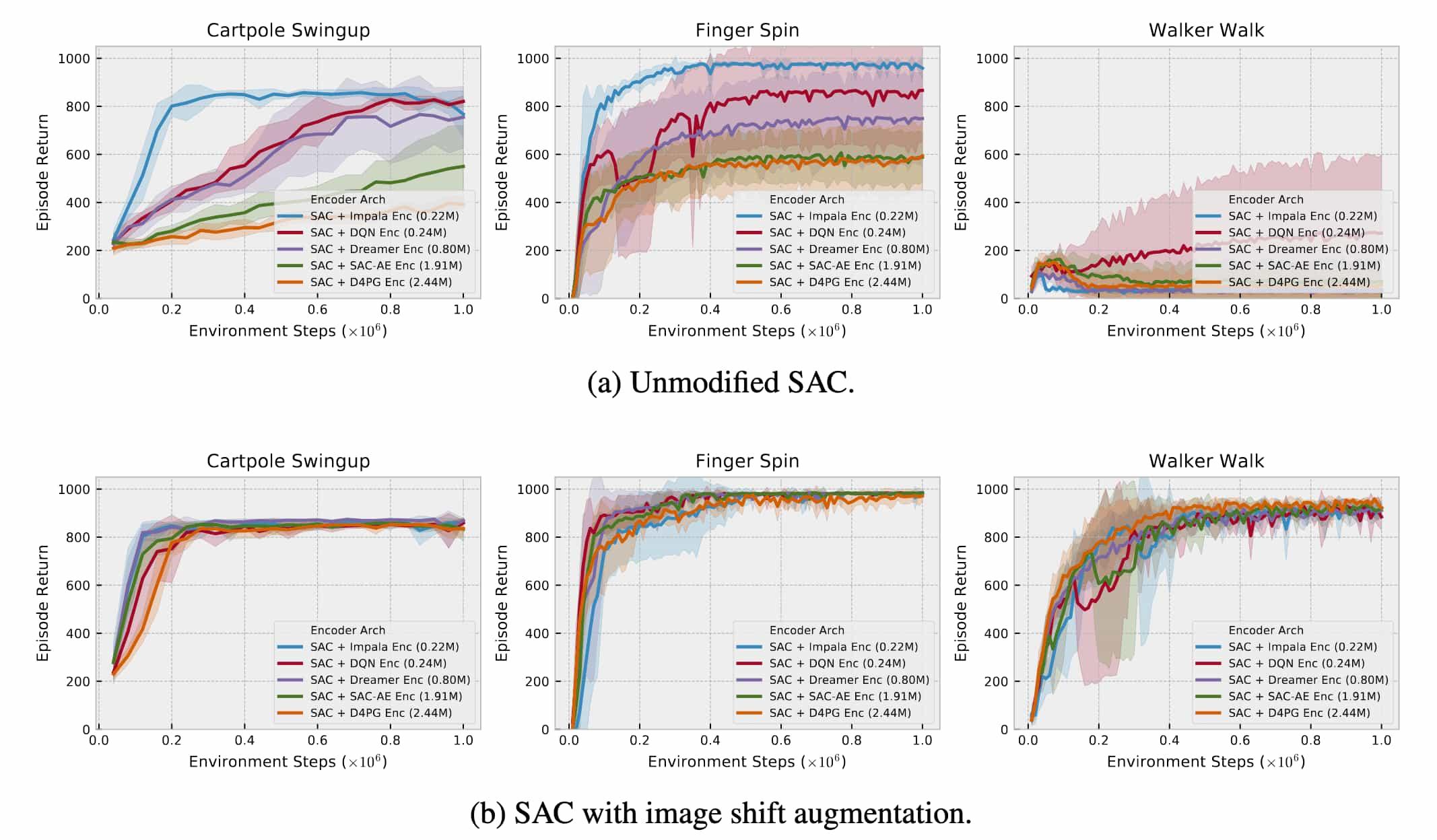
For unmodified SACs, task performance notably declines as encoder capacity increases, indicating overfitting. Particularly on the Walker Walk environment, all encoder architectures yield mediocre results, demonstrating the inability of SAC to train directly from pixels on harder problems. However, with random shifts, overfitting is substantially mitigated, closing the performance gap across encoder architectures. These random shifts alone enable SAC to reach competitive absolute performance levels without the need for auxiliary losses.

$\mathbf{Fig\ 8.}$ The performance of SAC trained from pixels on the DeepMind control suite using image encoder networks of different capacity (Kostrikov et al. 2020)

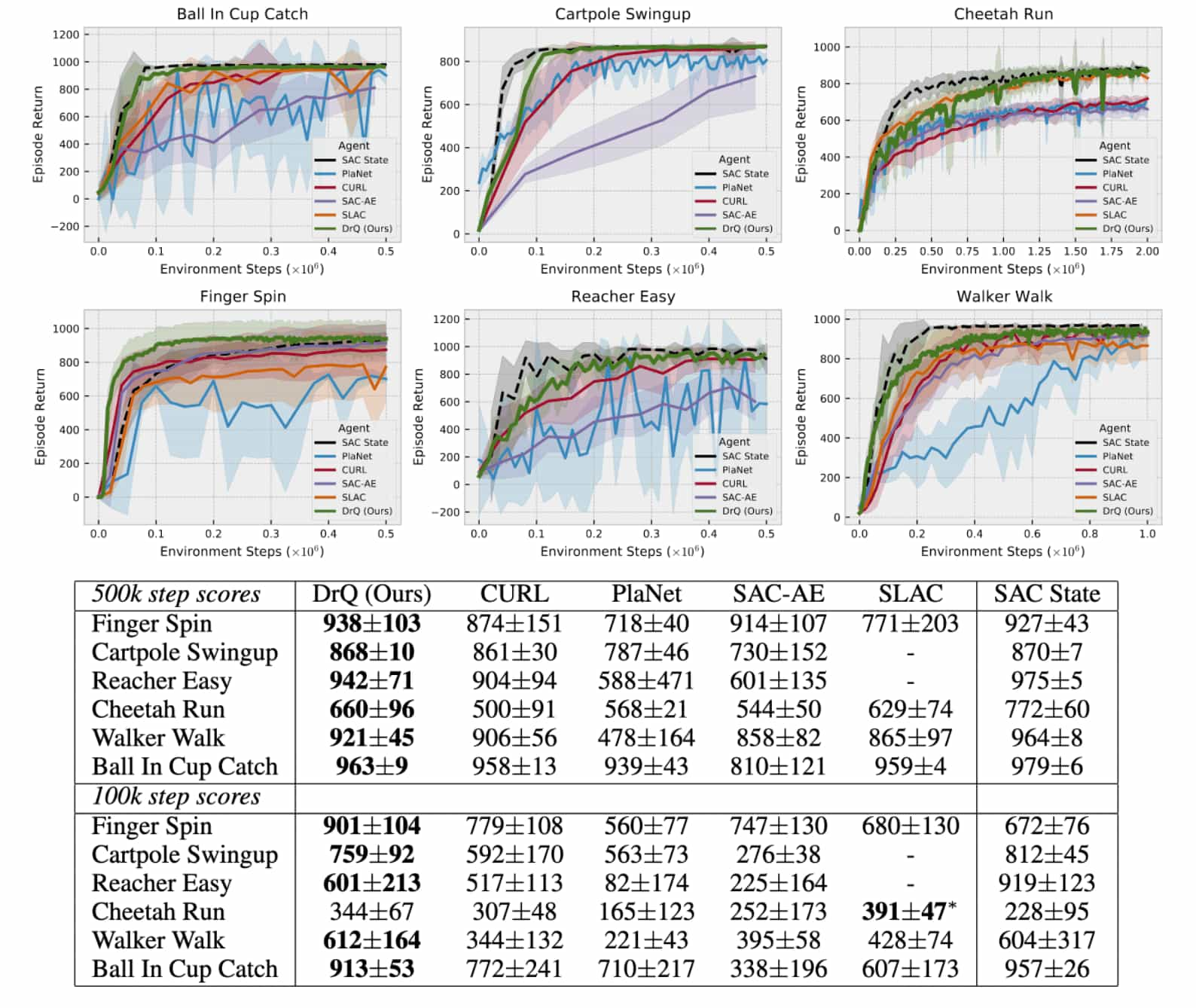
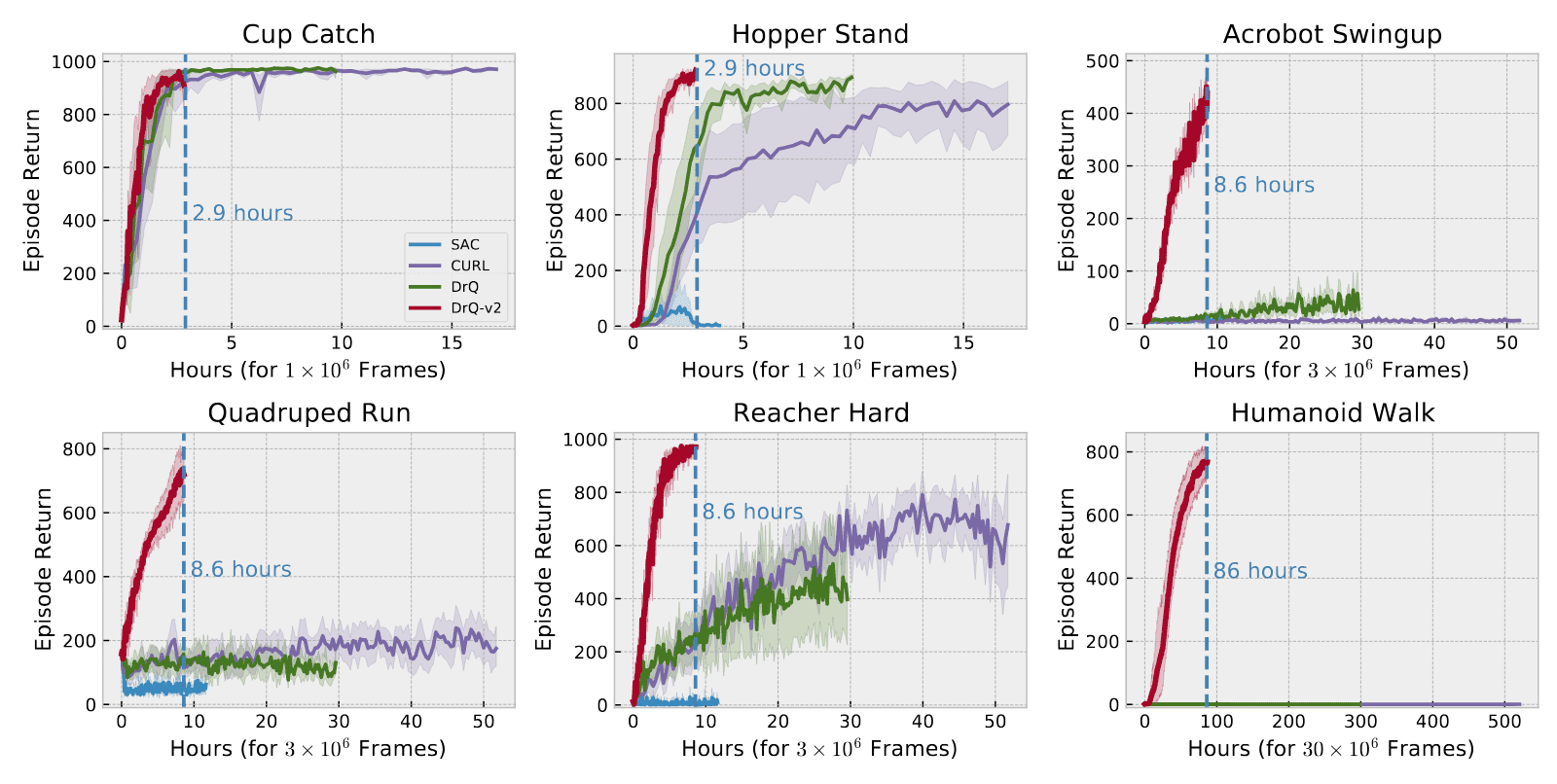
As a result, DrQ ($K=2$, $M=2$) outperforms other baselines in both the data-efficient ($100\text{k}$) and asymptotic performance ($500\text{k}$) regimes across six challenging control tasks from the Deepmind Control Suite. Furthermore, DrQ not only demonstrates superior sample-efficiency but also achieves faster performance in terms of wall-clock time.

$\mathbf{Fig\ 9.}$ The six challenging control tasks from DMC at $100\text{k}$ and $500\text{k}$ environment steps (Kostrikov et al. 2020)

DrQ-v2

DrQ-v2 builds on DrQ with several algorithmic adjustments to enhance its sample efficiency and performance on challenging visual control tasks:

(i) Replacing SAC with DDPG
(ii) DDPG allows us straightforwardly incorporating multi-step return
(iii) Bilinear interpolation to the random shift image augmentation
(iv) Exploration schedule
(v) Selecting better hyper-parameters including a larger capacity of the replay buffer.

Consequently, DrQ-v2 achieves state-of-the-art sample efficiency on tasks in the DeepMind Control Suite and stands out as the first model-free approach capable of solving pixel-based humanoid tasks.

$\mathbf{Fig\ 10.}$ DrQ-v2 framework and examples of walking and standing behaviors learned by DrQ-v2 for a complex humanoid agent from DMC (Yarats et al. 2022)

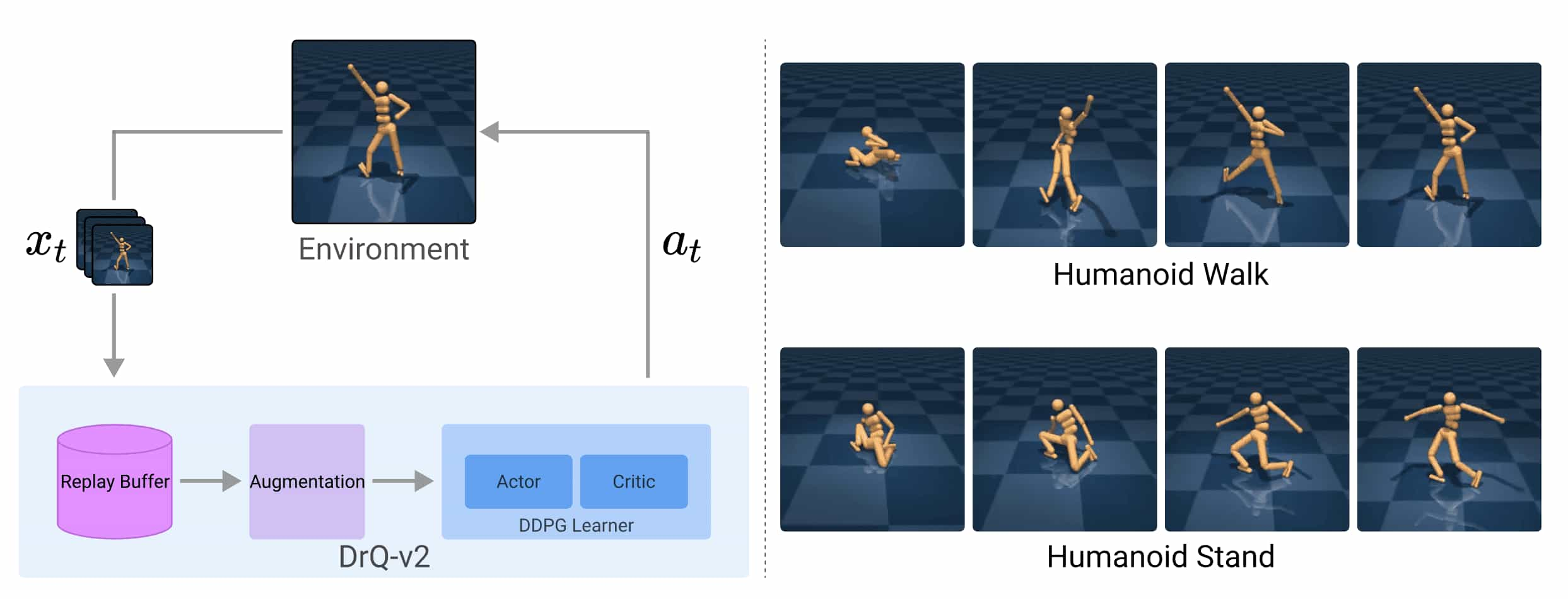
Improved Data-Augmented RL

The DrQ-v2 framework proceeds as follows:

1. Image encoder with Data Augmentation
   DrQ-v2 also applies random shifts to pixel observations of the environment. The augmented image observation is then embedded into a low-dimensional latent vector by applying a convolutional encoder $f_\xi$: $$ \mathbf{h}_t = f_\xi (\texttt{aug} (\mathbf{o}_t)) $$ Note that $f_\xi$ has the same encoder architecture as in DrQ, which first was introduced introduced in SAC-AE.
2. Actor-Critic Algorithm
   DrQ-v2 performs the DDPG actor-critic algorithm, augmented with $n$-step returns and clipped double Q-learning of TD3: $$ \mathcal{L} (\theta_k, \xi) = \mathbb{E}_{(\mathbf{o}_t, \mathbf{a}_t, r_{t:t+n-1}, \mathbf{o}_t) \sim \mathcal{D}} \left[ (Q_{\theta_k} (\mathbf{h}_t, \mathbf{a}_t) - y)^2 \right] \quad \forall k \in \{1, 2\} $$ where the TD target $y$ is defined as: $$ y = \sum_{\ell=0}^{n-1} \gamma^k r_{t + \ell} + \gamma^n \min_{k = 1, 2} Q_{\bar{\theta}_k} (\mathbf{h}_{t+n}, \mathbf{a}_{t+n}) $$ with the DDPG actor $\mathbf{a}_{t+n} = \pi_\phi (\mathbf{h}_{t+n}) + \varepsilon$ ($\varepsilon \sim \texttt{clip}(\mathcal{N}(0, \sigma^2), -c, c)$) and the target network EMA parameters $\bar{\theta}_1$, $\bar{\theta}_2$. The DDPG actor is trained to maximize the clipped Q-value: $$ \mathcal{L} (\phi) = - \mathbb{E}_{\mathbf{o}_t \sim \mathcal{D}} \left[ \min_{k=1, 2} Q_{\theta_k} (\mathbf{h}_t, \mathbf{a}_t) \right] $$
3. Scheduled Exploration Noise
   Empirically, the authors observed that varying exploration levels across different learning stages proves beneficial. They employed linear decay function $\sigma(t)$ to modulate the variance $\sigma^2$ of the exploration noise, defined as: $$ \sigma(t) = \sigma_\texttt{init} + (1 - \min (\frac{t}{T}, 1)) (\sigma_\texttt{final} - \sigma_\texttt{init}) $$ In the early stages of training, this schedule promotes a higher degree of stochasticity, allowing the agent to explore the environment more thoroughly. As training progresses and the agent has identified promising behaviors, the scheduler shifts toward determinism, enabling the agent to refine and master these behaviors.

$\mathbf{Fig\ 11.}$ DrQ-v2: Improved data-augmented RL (Yarats et al. 2022)

Experimental Results

As a result, DrQ-v2 outperforms prior model-free methods in sample efficiency across DMC easy, medium, and hard benchmarks. Notably, DrQ-v2’s advantage becomes especially evident on more challenging tasks (i.e., acrobot, quadruped, and humanoid), where exploration is especially challenging. Remarkably, DrQ-v2 is the first model-free method to solve the DMC humanoid locomotion tasks directly from pixel inputs.

$\mathbf{Fig\ 12.}$ Evaluating Sample Efficiency on DMC benchmarks (Yarats et al. 2022)

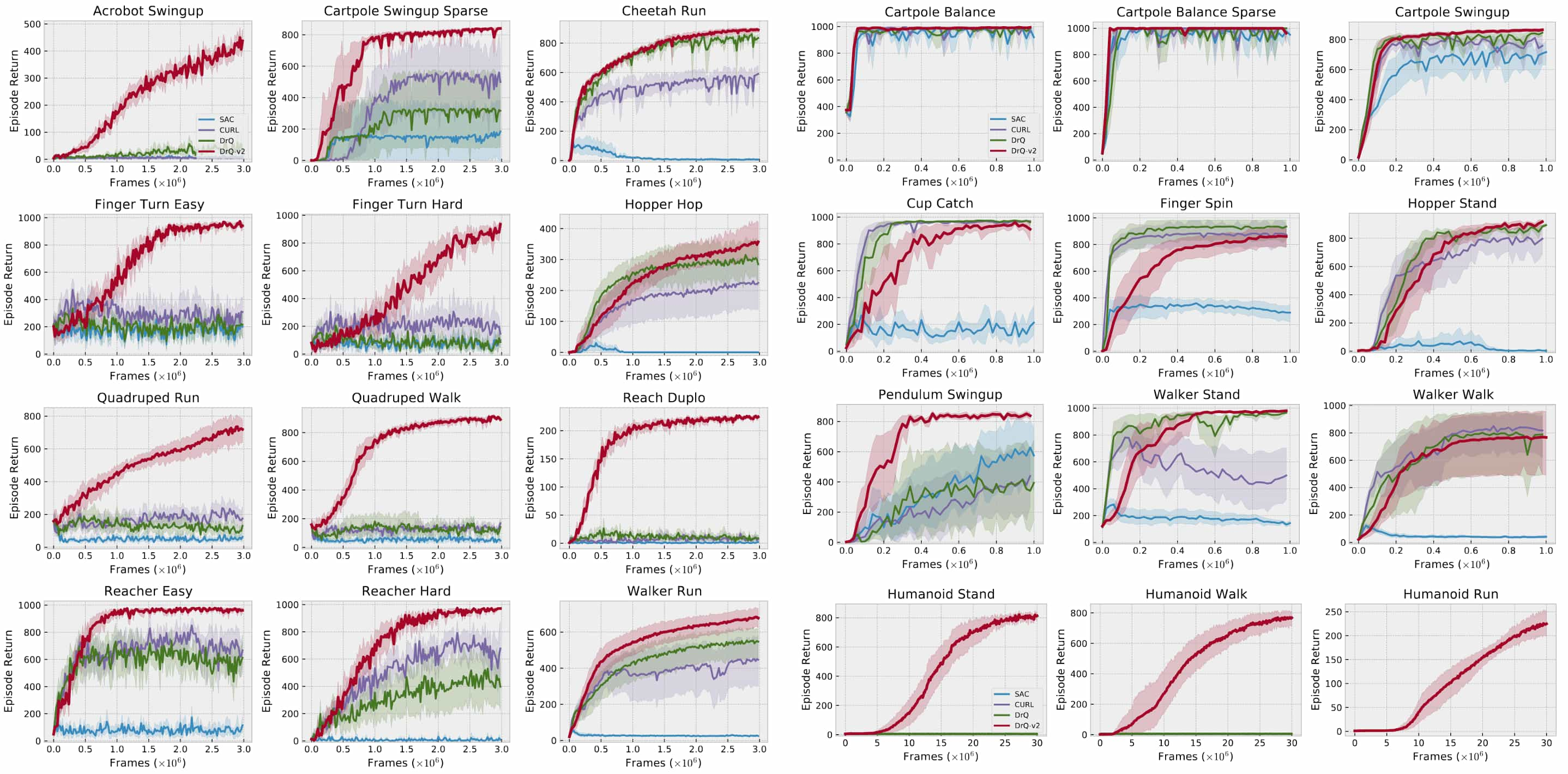
DrQ-v2 achieves superior sample efficiency compared to previous model-free methods while also requiring less wall-clock training time to attain this efficiency.

$\mathbf{Fig\ 13.}$ Evaluating Compute Efficiency on DMC benchmarks (Yarats et al. 2022)

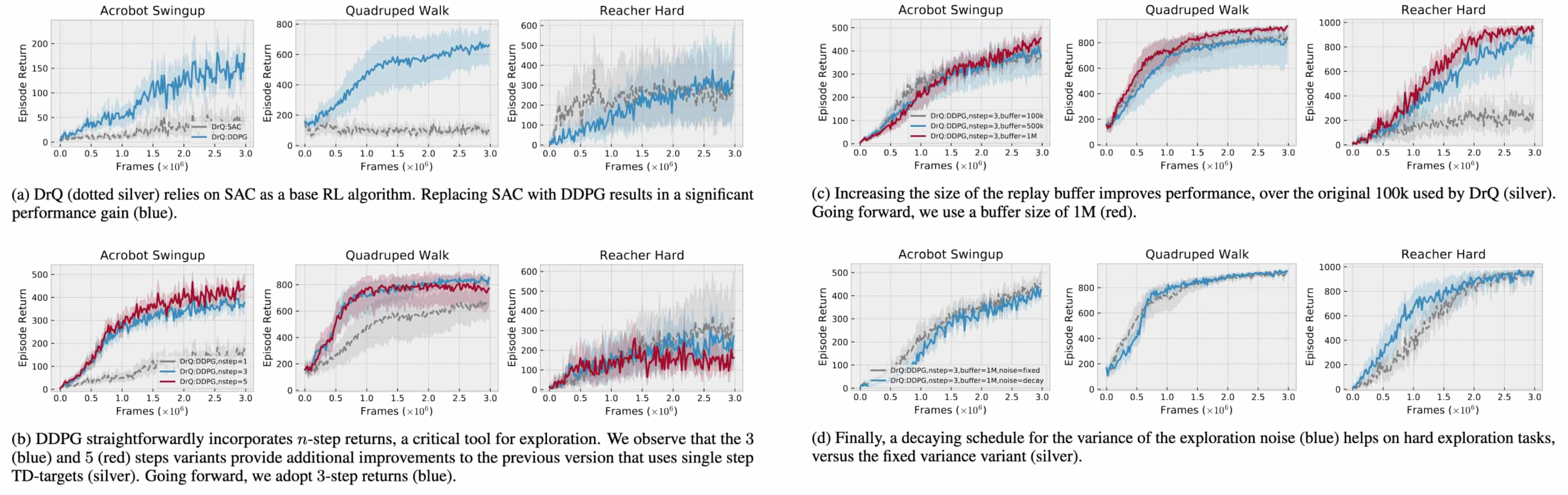
Lastly, the ablation studies justify the authors’ choices for DrQ-v2:

1. SAC v.s. DDPG
   SAC within DrQ encountered two notable limitations when addressing exploration-intensive, image-based tasks. (i) the automatic entropy adjustment strategy often proves insufficient, occasionally resulting in premature entropy collapse. This prevents the agent from discovering more optimal behaviors due to limited exploration. The second limitation involves soft Q-learning’s challenge in incorporating $n$-step returns to estimate TD error seamlessly.This is because computing target value for the soft $Q$-function requires estimating per-step entropy of the policy, which is a challenging task for large $n$ in the off-policy setting.
2. Replay Buffer Size
   A larger replay buffer plays an important role in circumventing the catastrophic forgetting problem. This issue is particularly prominent in tasks with more diverse initial state distributions (i.e., reacher or humanoid tasks), where the extensive range of possible behaviors necessitates substantially greater memory capacity.
3. Scheduled Exploration Noise
   Decaying the variance of exploration noise throughout training proves beneficial.

$\mathbf{Fig\ 14.}$ The ablation study of DrQ-v2 (Yarats et al. 2022)

References

[1] Laskin et al. “Reinforcement Learning with Augmented Data”, NeurIPS 2020
[2] Kostrikov et al. “Image Augmentation Is All You Need: Regularizing Deep Reinforcement Learning from Pixels”, NeurIPS 2020
[3] Yarats et al. “DrQ-v2: Improved Data-Augmented Reinforcement Learning”, ICLR 2022