[RL] MR.Q: Model-based Representations for Q-Learning

Model-based approaches, such as TD-MPC2, DreamerV3, and EfficientZeroV2 have recently showcased the potential of general-purpose algorithms, achieving impressive single-task performance on a diverse set of benchmarks without re-tuning hyperparameters. MR.Q algorithm introduced by Fujimoto et al. ICLR 2025 achieve competitive performance against SOTA domain-specific and generalist baselines with single hyperparameters. Interestingly, they claimed that the true benefit of model-based objectives is in the implicitly learned representation, rather than the model itself.

$\mathbf{Fig\ 1.}$ MR.Q: Model-based Representations for Q-Learning (Fujimoto et al. 2025)

MR.Q: Model-based Representations for Q-Learning

Model-based Representations for Q-Learning (MR.Q) is a model-free RL algorithm that learns an approximately linear representation of the value function through model-based objectives. It utilizes intermediate state \(\mathbf{z}_\mathbf{s}\) and state-action embeddings \(\mathbf{z}_\mathbf{sa}\):

\[\begin{array}[lr] f_\theta: \mathbf{s} \to \mathbf{z}_\mathbf{s} & g_\theta: (\mathbf{z}_\mathbf{s}, \mathbf{a}) \to \mathbf{z}_{\mathbf{sa}} \\ \pi_\phi: \mathbf{z}_\mathbf{s} \to \mathcal{A} & Q_\phi: \mathbf{z}_{\mathbf{sa}} \to \mathbb{R} \\ \end{array}\]

MR.Q performs an explicit representation learning stage can enable richer alternative learning signals that are grounded in the dynamics and rewards of the MDP, as opposed to relying exclusively on non-stationary value targets used in both value and policy learning.

$\mathbf{Fig\ 2.}$ Pseudocode of MR.Q (Fujimoto et al. 2025)

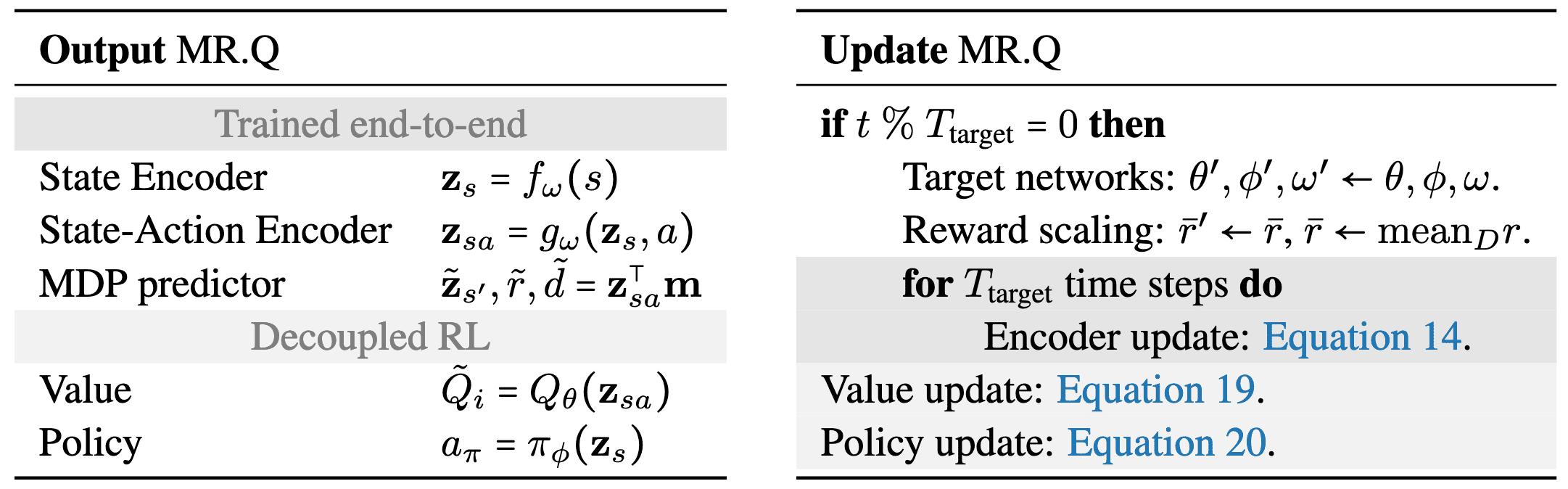
Encoders

The encoder loss is composed of three terms:

\[\begin{aligned} \mathcal{L}_{\texttt{encoder}}(f, g, \mathbf{m}) := \sum_{t=1}^{n_{\texttt{enc}}} & \lambda_{\texttt{reward}} \mathcal{L}_{\texttt{reward}}(\hat{r}_t) \\ & +\lambda_{\texttt{dynamics}} \mathcal{L}_{\texttt{dynamics}}(\hat{\mathbf{z}}_{\mathbf{s}_t}) \\ & + \lambda_{\texttt{terminal}} \mathcal{L}_{\texttt{terminal}}(\hat{d}_t) \end{aligned}\]

where the model is unrolled by encoding:

\[\hat{\mathbf{z}}_{\mathbf{s}_t}, \hat{r}_t, \hat{d}_t := g_\theta (\hat{\mathbf{z}}_{\mathbf{s}_{t-1}}, \mathbf{a}_{t-1})^\top \mathbf{m} \quad \text { where } \quad \hat{\mathbf{z}}_{\mathbf{s}_0} = f_\theta (\mathbf{s}_0)\]

based on a subsequence of an episode:

\[\{(\mathbf{s}_0, \mathbf{a}_0, r_1, d_1, \mathbf{s}_1, \cdots, r_{n_{\texttt{enc}}}, d_{n_{\texttt{enc}}}, \mathbf{s}_{n_{\texttt{enc}}}) \}\]

1. Reward Prediction
   For stable prediction across a wide range of reward magnitudes, the authors formulate the reward prediction task as a classification problem in a $\log$-transformed space, instead of regression, utilizing soft-target cross entropy loss: $$ \mathcal{L}_{\texttt{reward}}(\hat{r}_t) := \texttt{CE} (\hat{r}_t, \texttt{two-hot} (r (\mathbf{s}_t, \mathbf{a}_t))) $$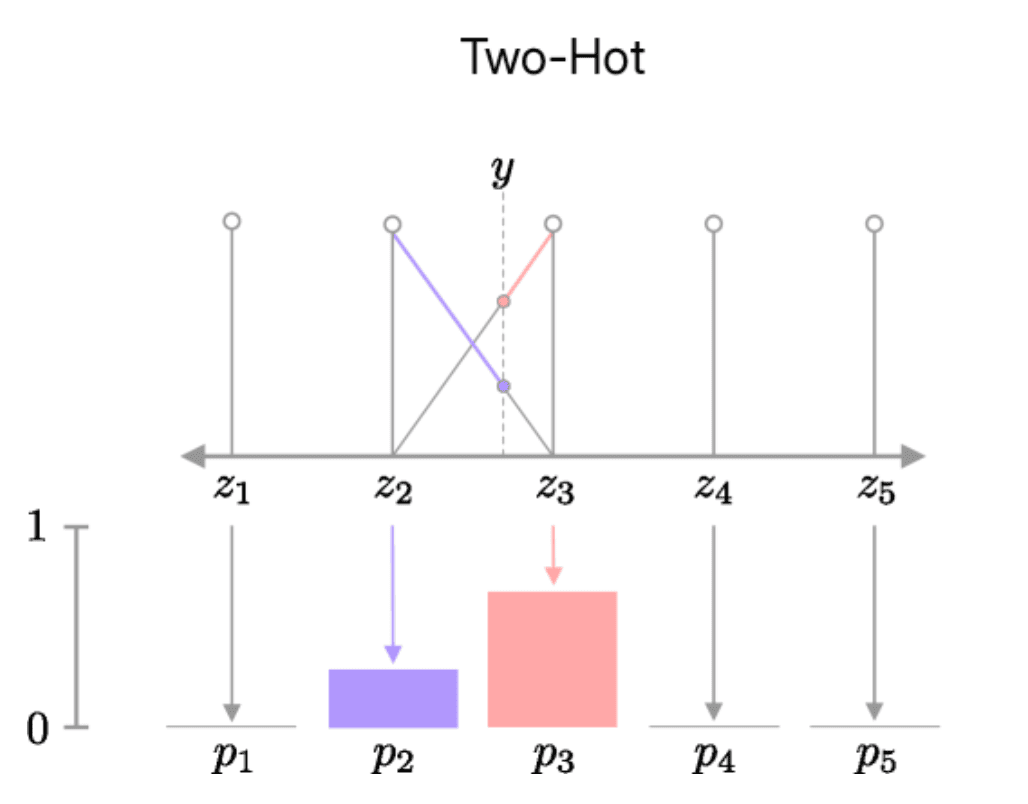

   
   

   $\mathbf{Fig\ 3.}$ Two-hot encoding (Farebrother et al. 2024)
   
   To handle a wide range of reward magnitudes without prior knowledge, the locations of the two-hot encoding are spaced at increasing non-uniform intervals ($\exp$-transformed space) using $\mathrm{symexp}$: $$ \mathrm{symexp} (x) = \mathrm{sign}(x)(e^x − 1) $$
2. Dynamics Loss
   The dynamics loss minimizes the MSE between the predicted next state embedding $\hat{\mathbf{z}}_{\mathbf{s}_{t+1}}$ and the next state embedding $\bar{\mathbf{z}}_{\mathbf{s}_{t+1}}$ from the target encoder $f_{\theta_\texttt{target}}$: $$ \mathcal{L}_{\texttt{dynamics}}(\hat{\mathbf{z}}_{\mathbf{s}_{t}}) := \left( \hat{\mathbf{z}}_{\mathbf{s}_{t}} - f_{\theta_\texttt{target}} (\mathbf{s}_{t}) \right)^2 $$
3. Terminal Prediction
   MR.Q also encodes the termination by repeating the dynamics loss where the target is maksed by the binary terminal signal $d_t$: $$ \mathcal{L}_{\texttt{terminal}}(\hat{d}_t) := \left( \hat{d}_t - d_t \cdot f_{\theta_\texttt{target}} (\mathbf{s}_{t+1}) \right)^2 $$ where $d_t = 0$ for the terminal transition. Therefore, the target is set to the $0$-vector if the transition is terminal. This form of loss allows for a dense learning signal even when the terminal function is highly sparse.

Note that the encoder network is implemented with convolution layers for image inputs instead of MLP for state vector inputs:

$\mathbf{Fig\ 4.}$ Encoder network architecture (Fujimoto et al. 2025)

Actor: DDPG

The actor of MR.Q is implemented with DDPG:

\[\mathbf{a}_\pi = \begin{cases} \arg \max \; \mathbf{a} & \quad \text{ discrete } \mathcal{A} \\ \text{clip} (\mathbf{a}, -1, 1) & \quad \text{ continuous } \mathcal{A} \\ \end{cases}\]

where:

\[\mathbf{a} = \pi_\phi (\mathbf{s}) + \text{clip} (\varepsilon, -c, c), \quad \varepsilon \sim \mathcal{N} (0, \sigma^2)\]

Discrete actions are represented by a one-hot encoding, where the Gaussian noise is added to each dimension. Action noise and the clipping is scaled according the range of the action space. Then, the policy is updated using the deterministic policy gradient:

\[\mathcal{L}_\texttt{actor} (\mathbf{a}_\pi) := -\frac{1}{2} \sum_{i = 1, 2} \hat{Q}_{\theta_i} (\mathbf{z}_{\mathbf{s} \mathbf{a}_\pi}) + \lambda_\texttt{pre-activ} \mathbf{z}_\pi^2\]

Note that a small regularization penalty is added to the square of the pre-activations \(\mathbf{z}_\pi^2\) before the policy’s final activation ($\texttt{softmax}$ for discrete space, $\tanh$ for continuous space) to help avoid local minima when the reward, and value, is sparse. In other words, \(\mathbf{a} = \texttt{activ}(\mathbf{z}_\pi)\).

Critic: TD7

The critic of MR.Q is trained using Huber loss similar to LAP loss of TD7, but with clipped double target Q (CDQ) of TD3:

\[\mathcal{L}_\texttt{critic} (\hat{Q}_{\theta_i}) := \texttt{Huber} \left( \hat{Q}_{\theta_i}, \frac{1}{\bar{r}} \left( \sum_{t=0}^{n_Q - 1} \gamma^t r (\mathbf{s}_t, \mathbf{a}_t) + \gamma^{n_Q} \bar{Q} \right) \right), \quad \bar{Q} := \bar{r}^\prime \min_{j = 1, 2} Q_{\theta_{\texttt{target}, j}} ( \mathbf{z}_{\mathbf{s}_{n_Q} \mathbf{a}_{\pi_{\phi_\texttt{target}}}})\]

where the $\arg \max$ action \(\mathbf{a}_{\pi_{\phi_\texttt{target}}}\) of target Q is selected by the target actor $\pi_{\phi_\texttt{target}}$. The value $\bar{r}^\prime$ captures the target average absolute reward, which is the scaling factor used to the most recently copied value functions $Q_{\theta_i}$. This value is updated simultaneously with the target networks $\bar{r}^\prime \leftarrow \bar{r}$, and $\bar{r}$ is then updated to the new average of the buffer $\mathcal{D}$: $\bar{r} \leftarrow \texttt{mean}_\mathcal{D} r$. Maintaining a consistent reward scale keeps the loss magnitude constant across different benchmarks, thus improving the robustness of a single set of hyperparameters.

Experimental Results

MR.Q show a competitive performance on a variety of common RL benchmarks with a single set of hyperparameters:

$\mathbf{Fig\ 5.}$ Single hyperparamters for MR.Q (Fujimoto et al. 2025)

Performances

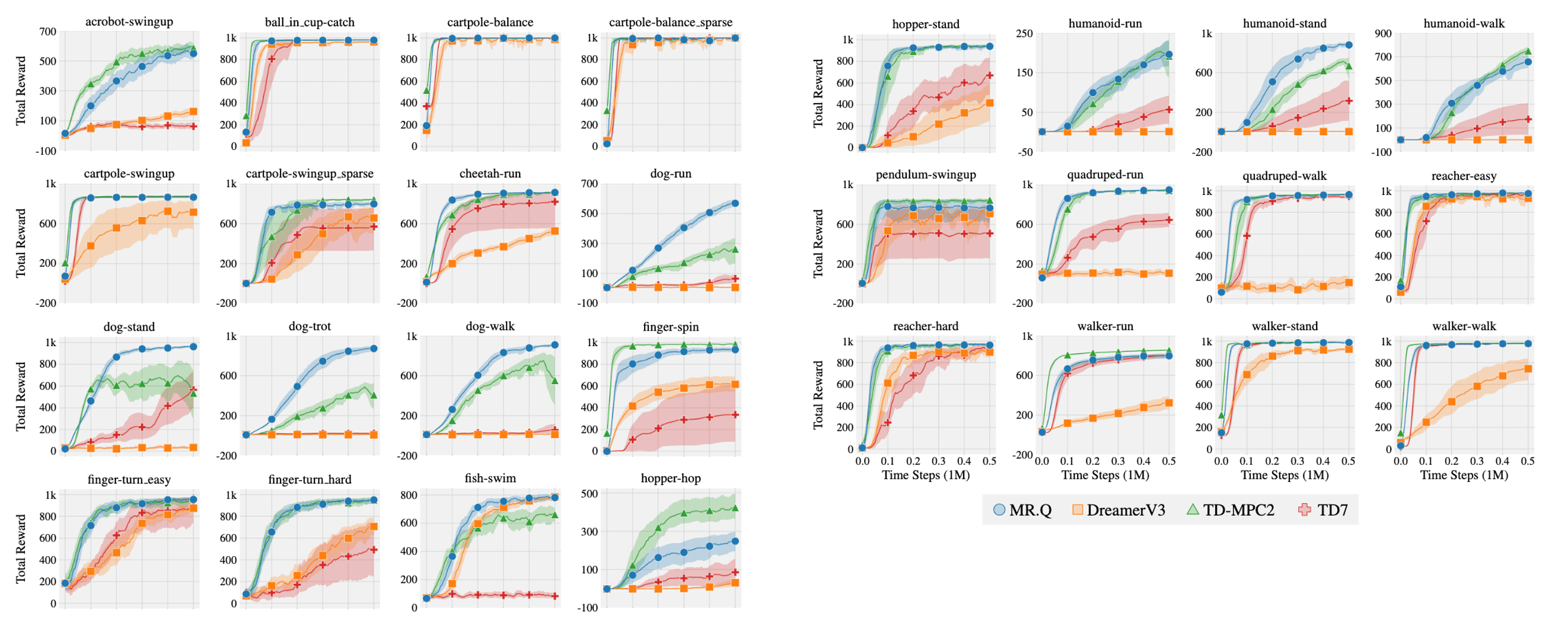
The authors observed the presence of “no free lunch”, where the best-performing baseline in one benchmark often fails to replicate its success in another. Regardless, MR.Q achieves the highest performance across both DMC benchmarks, demonstrating its adaptability to varying observation spaces. Although it falls slightly behind TD7 in the Gym benchmark, MR.Q emerges as the strongest overall method across all continuous control benchmarks. In the Atari benchmark, DreamerV3 surpasses MR.Q but does so with a model possessing 40 times more parameters and performs poorly in other benchmarks. Compared to model-free baselines, MR.Q outperforms both DQN and Rainbow, showcasing its efficacy in discrete action spaces.

$\mathbf{Fig\ 6.}$ Results summary (Fujimoto et al. 2025)

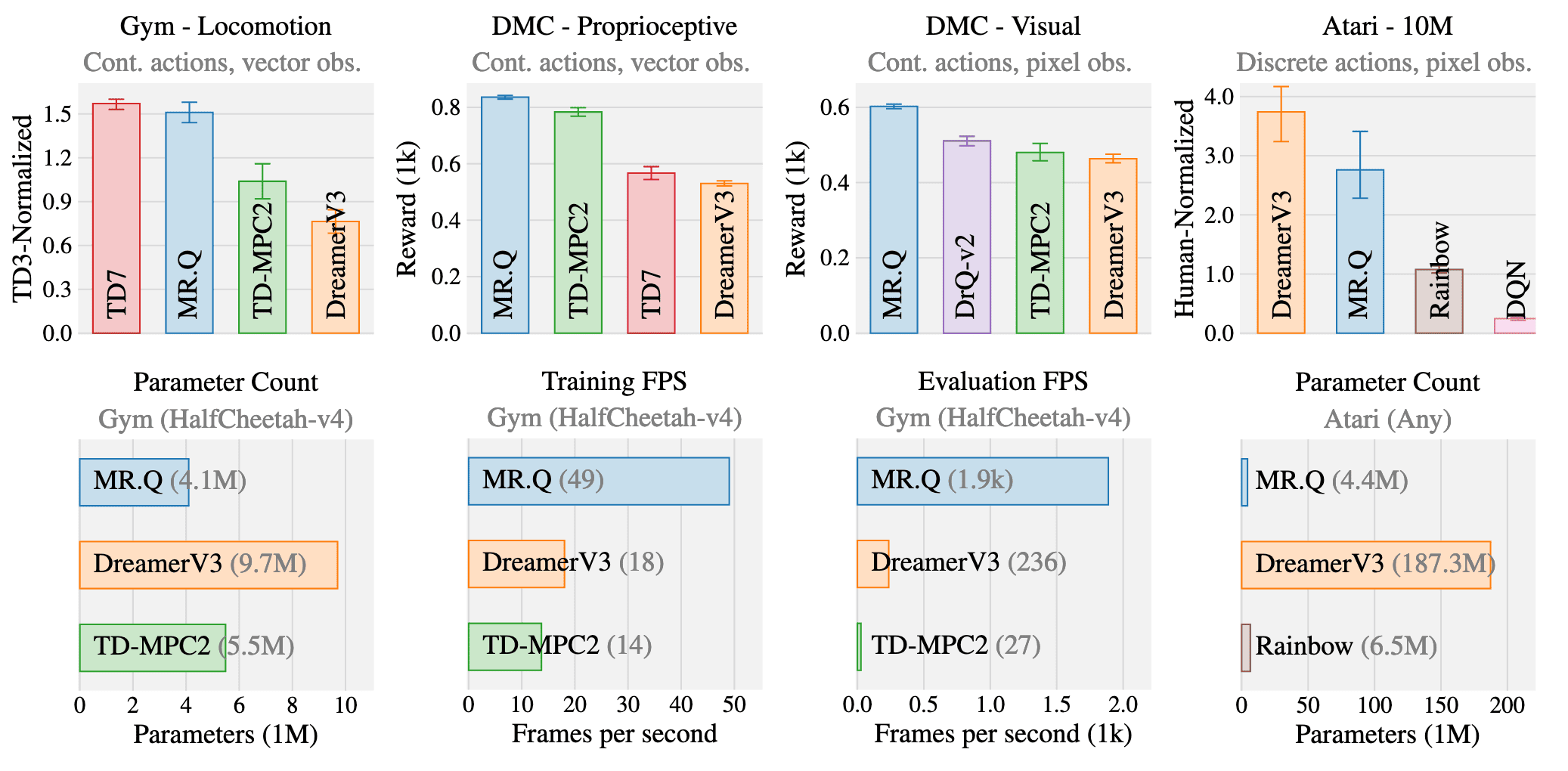
DeepMind Control (DMC) Suite

$\mathbf{Fig\ 7.}$ Learning curves on state-based DMC (Fujimoto et al. 2025)

$\mathbf{Fig\ 8.}$ Learning curves on vision-based DMC (Fujimoto et al. 2025)

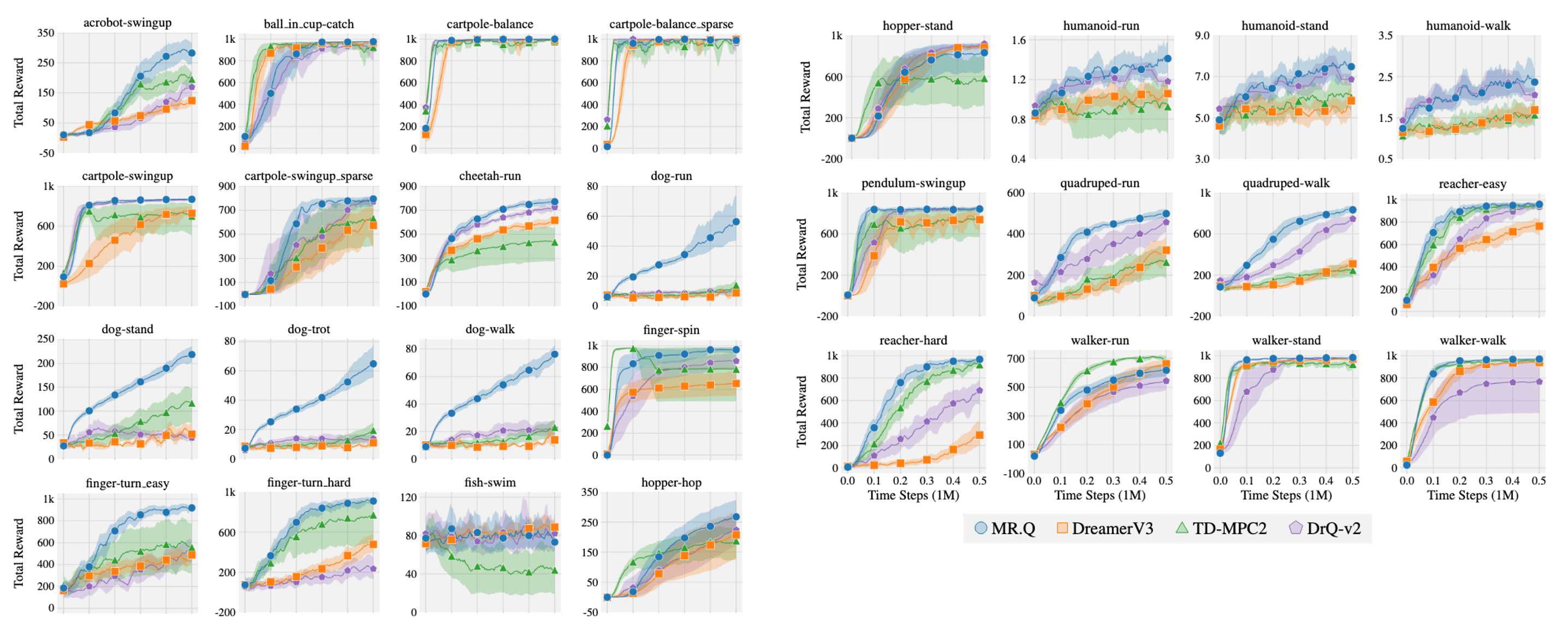
Gym

$\mathbf{Fig\ 9.}$ Gym results (Fujimoto et al. 2025)

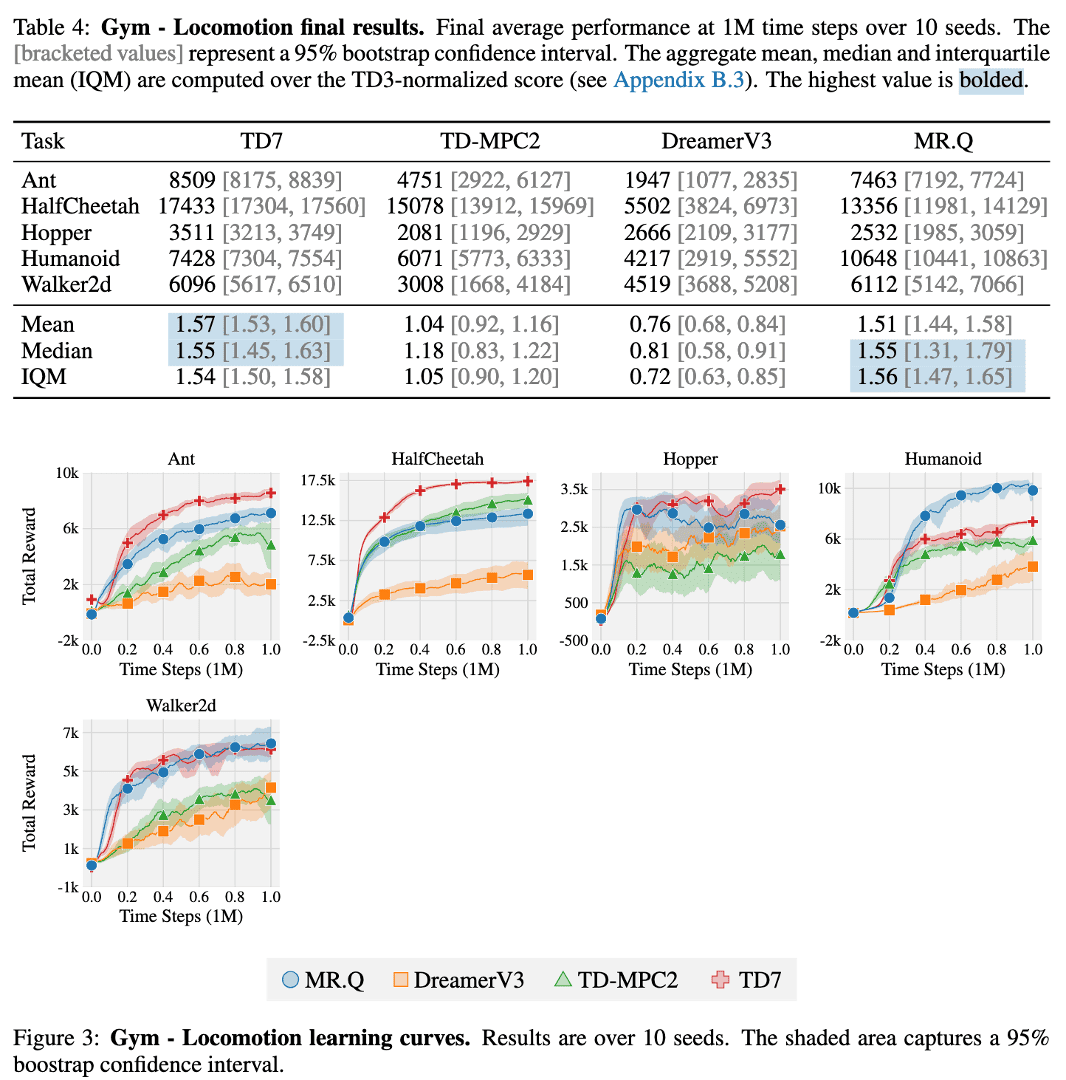
Atari

$\mathbf{Fig\ 10.}$ Learning curves on Atari (Fujimoto et al. 2025)

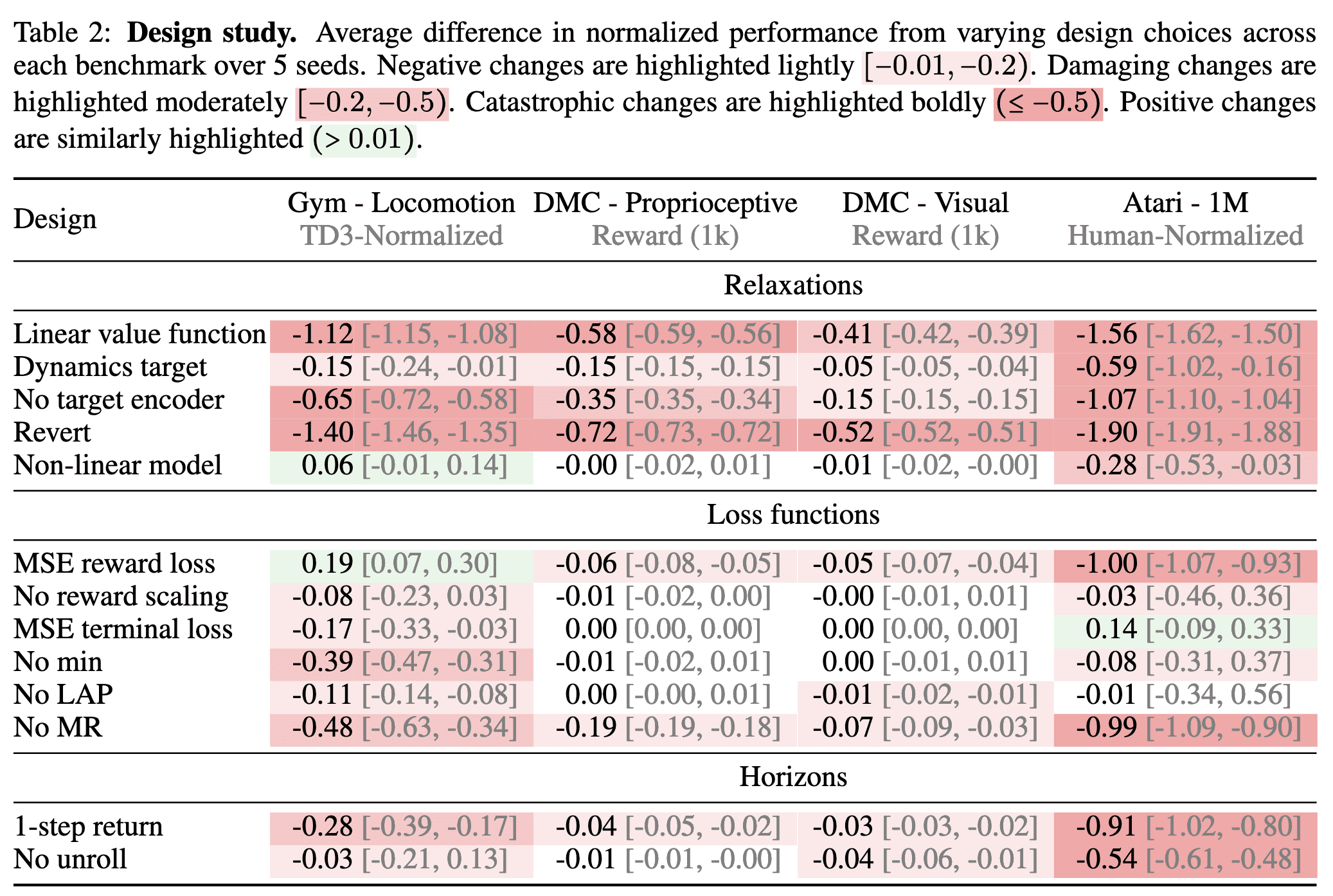
Design Study

The following table shows the impact of various design choices and hyperparameters of MR.Q.

• Linear value function: all of the aforementioned changes simultaneously;
• Dynamics target: replace the next state target \(\mathbf{z}_{\mathbf{s}^\prime}\) to the dynamics target \(\mathbf{z}_{\mathbf{s}^\prime \mathbf{a}^\prime}\);
• No target encoder: use the current online encoder to generate the dynamics target \(\mathbf{z}_{\mathbf{s}^\prime \mathbf{a}^\prime}\);
• Revert: all of the aforementioned changes simultaneously;
• Non-linear model: use non-linear network for model-based representation learning;
• No reward scaling: set $\bar{r} = \bar{r}^\prime = 1$;
• No min: remove CDQ;
• No LAP: remove Huber loss and use MSE;
• No MR: remove the model-based representation learning;
• 1-step returns: set $n_Q = 1$;
• No unroll: set $n_\texttt{enc} = 1$;

$\mathbf{Fig\ 11.}$ Design study of MR.Q (Fujimoto et al. 2025)

Theoretical Motivation

Preliminary: Semi-Gradient TD (SGTD)

For training data pairs \(\left\langle \mathbf{s}_1, r (\mathbf{s}_1, \mathbf{a}_1) + \gamma \widehat{v}(\mathbf{s}_{2}; \mathbf{w}) \right\rangle, \left\langle \mathbf{s}_2, r (\mathbf{s}_2, \mathbf{a}_2) + \gamma \widehat{v}(\mathbf{s}_3; \mathbf{w}) \right\rangle, \cdots, \left\langle \mathbf{s}_{T-1}, r (\mathbf{s}_{T-1}, \mathbf{a}_{T-1}) \right\rangle\), the parameter update step is given by:

\[\begin{aligned} \Delta \mathbf{w} = \alpha \cdot (\underbrace{r (\mathbf{s}, \mathbf{a}) + \gamma \widehat{v}(\mathbf{s}^\prime; \mathbf{w})}_{\approx \; v_\pi (\mathbf{s})} - \widehat{v}(\mathbf{s}; \mathbf{w})) \cdot \nabla_{\mathbf{w}} \widehat{v}(\mathbf{s}; \mathbf{w}) \end{aligned}\]

$\mathbf{Fig\ 12.}$ The pseudocode for Semi-gradient TD (SGTD)

However, convergence cannot always be guaranteed when using a bootstrapping estimate as the target. Bootstrapping targets, such as n-step returns $G_{t: t+ n}$ or the TD target, inherently depend on the current parameter $\mathbf{w}$. This dependency makes them biased approximations of the true value function $v_\pi$​. Moreover, the discussion so far is based on the reasonable belief that the target $v_\pi$ and $q_\pi$ are independent of $\mathbf{w}$, i.e., $\nabla_{\mathbf{w}} v_\pi (\mathbf{s}) = 0$. Therefore, for TD learning that approximates $v_\pi (\mathbf{s}) \approx r + \gamma \hat{v} (\mathbf{s}; \mathbf{w})$, we usually assume that $\nabla_{\mathbf{w}} v_\pi (\mathbf{s}) = 0$ and obtain the following gradient:

\[\begin{aligned} \nabla_{\mathbf{w}} \mathcal{L} (\mathbf{w}) & = \nabla_{\mathbf{w}} \mathbb{E}_\pi \left[ \left(v_\pi (\mathbf{s}) - \widehat{v}(\mathbf{s}; \mathbf{w}) \right)^2 \right] \\ & =\mathbb{E}_\pi \left[ \nabla_{\mathbf{w}} \left(v_\pi (\mathbf{s}) - \widehat{v}(\mathbf{s}; \mathbf{w}) \right)^2 \right] \\ & \propto \mathbb{E}_\pi \left[ \left(v_\pi (\mathbf{s}) - \widehat{v}(\mathbf{s}; \mathbf{w})\right) \cdot \nabla_{\mathbf{w}} \left(v_\pi (\mathbf{s}) - \widehat{v}(\mathbf{s}; \mathbf{w}) \right) \right] & \text{ where } v_\pi (\mathbf{s}) \approx r + \gamma \hat{v} (\mathbf{s}; \mathbf{w}) \\ & = \mathbb{E}_\pi \left[ \left(v_\pi (\mathbf{s}) - \widehat{v}(\mathbf{s}; \mathbf{w}) \right) \cdot \nabla_{\mathbf{w}} \widehat{v}(\mathbf{s}; \mathbf{w}) \right] & \because \text{ assuming } \nabla_{\mathbf{w}} v_\pi (\mathbf{s}) = 0 \\ \end{aligned}\]

Hence, our update is not the true gradient descent and includes only a part of the gradient, ignoring the effect of $\mathbf{w}$ on the target. Due to this reason, this algorithm is commonly referred to as semi-gradient TD methods.

Model-Based Representations for Q-Learning

For theoretical insight, we will suppose a linear Q-value function $Q(\mathbf{s}, \mathbf{a})$ that is decomposable by state-action features \(\mathbf{z}_\mathbf{sa}\) and weights $\mathbf{w}$:

\[Q(\mathbf{s}, \mathbf{a}) = \mathbf{z}_{\mathbf{sa}}^\top \mathbf{w}\]

Consider a model-free update based on semi-gradient TD:

\[\mathbf{w} \leftarrow \mathbf{w} - \alpha \cdot \mathbb{E}_\mathcal{D} \left[ \nabla_\mathbf{w} \left( \mathbf{z}_\mathbf{sa}^\top \mathbf{w} - \texttt{sg} ( r(\mathbf{s}, \mathbf{a}) + \gamma \cdot \mathbf{z}_\mathbf{s^\prime a^\prime}^\top \mathbf{w} ) \right)^2 \right]\]

and a model-based approach based on rolling out linear estimates of the dynamics \(\hat{\mathbf{z}}_{\mathbf{s}^\prime \mathbf{a}^\prime} = \mathbf{z}_\mathbf{sa}^\top \mathbf{W}_d\) and reward \(\hat{r} = \mathbf{z}_\mathbf{sa}^\top \mathbf{w}_r\):

\[\begin{aligned} Q (\mathbf{s}_t, \mathbf{a}_t) & = r (\mathbf{s}_t, \mathbf{a}_t) + \sum_{n=1}^\infty \gamma^{n} r (\mathbf{s}_{t+n}, \mathbf{a}_{t+n}) \\ & = \mathbf{z}_{\mathbf{sa}}^\top \mathbf{w}_r + \sum_{n=1}^\infty \gamma^{n} \left( \mathbf{z}_{\mathbf{sa}}^\top \mathbf{W}_d^n \right)^\top \mathbf{w}_r \\ & \equiv \mathbf{z}_{\mathbf{sa}}^\top \mathbf{w} \end{aligned}\]

where

\[\begin{aligned} & \mathbf{w}= \sum_{t=0}^{\infty} \gamma^t \mathbf{W}_d^t \mathbf{w}_r=\left(\mathbf{I}-\gamma \mathbf{W}_d\right)^{-1} \mathbf{w}_r, \\ & \mathbf{w}_r=\underset{\mathbf{w}_r}{\arg \min} \; \mathbb{E}_\mathcal{D} \left[\left(\mathbf{z}_{\mathbf{sa}}^{\top} \mathbf{w}_r- r(\mathbf{s}, \mathbf{a}) \right)^2\right] \in \mathbb{R}^{(\vert \mathcal{S} \vert \times \vert \mathcal{A} \vert)}, \quad \mathbf{W}_d=\underset{\mathbf{W}_d}{\arg \min} \; \mathbb{E}_\mathcal{D} \left[\left(\mathbf{z}_{\mathbf{sa}}^{\top} \mathbf{W}_d-\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}\right)^2\right] \in \mathbb{R}^{(\vert \mathcal{S} \vert \times \vert \mathcal{A} \vert) \times (\vert \mathcal{S} \vert \times \vert \mathcal{A} \vert)} \end{aligned}\]

Then, we can show that these model-free and model-based approaches are equivalent:

$\color{red}{\mathbf{Theorem.}}$ Equivalence between model-free and model-based learning
The fixed point of the model-free approach and the solution of the model-based approach are the same: $$ \mathbf{w}^* = \left( \mathbf{Z}^\top \mathbf{Z} - \gamma \mathbf{Z}^\top \mathbf{Z}^\prime \right)^{-1} \mathbf{Z} \mathbf{r} $$ where $\mathbf{Z}, \mathbf{Z}^\prime \in \mathbb{R}^{(\vert \mathcal{S} \vert \times \vert \mathcal{A} \vert) \times d}$ is a matrix containing current and next state-action embeddings $\mathbf{z}_\mathbf{sa}, \mathbf{z}_{\mathbf{s}^\prime \mathbf{a}^\prime} \in \mathbb{R}^d$, and $\mathbf{r} \in \mathbb{R}^{(\vert \mathcal{S} \vert \times \vert \mathcal{A} \vert)}$ is the vector of corresponding rewards $r(\mathbf{s}, \mathbf{a})$ for each state-action pair $(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}$.

$\mathbf{Proof.}$

We can write the linear semi-gradient TD update at timestep $t$ as follows:

\[\begin{aligned} \mathbf{w}_{t+1} & = \mathbf{w}_t - \alpha \mathbf{Z}^\top \left( \mathbf{Z} \mathbf{w}_t - \left( \mathbf{r} + \gamma \mathbf{Z}^\prime \mathbf{w}_t \right) \right) \\ & = \mathbf{w}_t - \alpha \mathbf{Z}^\top \mathbf{Z} \mathbf{w}_t + \alpha \mathbf{Z}^\top \mathbf{r} + \alpha \gamma \mathbf{Z}^\top \mathbf{Z}^\prime \mathbf{w}_t \\ & = \left( \mathbf{I} - \alpha \left( \mathbf{Z}^\top \mathbf{Z} - \gamma \mathbf{Z}^\top \mathbf{Z}^\prime \right) \right) \mathbf{w}_t + \alpha \mathbf{Z}^\top \mathbf{r} \end{aligned}\]

The fixed point of the system is then given by:

\[\begin{gathered} \mathbf{w}^* = \left(\mathbf{I} - \alpha \left( \mathbf{Z}^\top \mathbf{Z} - \gamma \mathbf{Z}^\top \mathbf{Z}^\prime \right) \right) \mathbf{w}^* + \alpha \mathbf{Z}^\top \mathbf{r} \\ \Downarrow \\ \mathbf{w}^* = \left( \mathbf{Z}^\top \mathbf{Z} - \gamma \mathbf{Z}^\top \mathbf{Z}^\prime \right)^{-1} \mathbf{Z} \mathbf{r} \end{gathered}\]

In case of model-based learning, the least squares solution to $\mathbf{W}_d$ and $\mathbf{w}_r$ are given by:

\[\begin{aligned} \mathbf{W}_d = \left( \mathbf{Z}^\top \mathbf{Z} \right)^{-1} \mathbf{Z}^\top \mathbf{Z}^\prime \\ \mathbf{w}_r = \left( \mathbf{Z}^\top \mathbf{Z} \right)^{-1} \mathbf{Z}^\top \mathbf{r} \end{aligned}\]

By rolling out $\mathbf{W}_d$ and $\mathbf{w}_r$, the model-based solution can be obtained:

\[Q = \mathbf{Z} \underbrace{\sum_{t=0}^\infty \gamma^t \mathbf{W}_d^t \mathbf{w}_r}_{\mathbf{w}^*}\]

Simplifying $\mathbf{w}^*$:

\[\begin{aligned} \mathbf{w}^* & = \left(\mathbf{I}-\gamma \mathbf{W}_d\right)^{-1} \mathbf{w}_r \\ \mathbf{w}^* & = \left(\mathbf{I}- \gamma \left( \mathbf{Z}^\top \mathbf{Z} \right)^{-1} \mathbf{Z}^\top \mathbf{Z}^\prime \right)^{-1} \left( \mathbf{Z}^\top \mathbf{Z} \right)^{-1} \mathbf{Z}^\top \mathbf{r} \\ \mathbf{Z}^\top \mathbf{Z} \left(\mathbf{I}- \gamma \left( \mathbf{Z}^\top \mathbf{Z} \right)^{-1} \mathbf{Z}^\top \mathbf{Z}^\prime \right) \mathbf{w}^* & = \mathbf{Z}^\top \mathbf{r} \\ \left( \mathbf{Z}^\top \mathbf{Z} - \gamma \mathbf{Z}^\top \mathbf{Z}^\prime \right) \mathbf{w}^* & = \mathbf{Z} \mathbf{r} \\ \end{aligned}\] \[\tag*{$\blacksquare$}\]

Therefore, we can relate the value estimation accuracy with the accuracy of reward and dynamics components of the estimated model. The following theorem shows that the value error is bounded by the accuracy of the estimated dynamics and reward:

$\color{red}{\mathbf{Theorem.}}$ Boundedness of Value Error
Define the value error $\texttt{VE}$ under the policy $\pi$ as follows: $$ \texttt{VE} (\mathbf{s}, \mathbf{a}) := Q (\mathbf{s}, \mathbf{a}) - Q^\pi (\mathbf{s}, \mathbf{a}) = \mathbf{z}_\mathbf{sa}^\top \mathbf{w} - Q^\pi (\mathbf{s}, \mathbf{a}) $$ Then, the value error of the solution $\mathbf{w}^*$ is bounded by the accuracy of the estimated dynamics and reward: $$ \vert \texttt{VE}(\mathbf{s}, \mathbf{a}) \vert \leq \frac{1}{1-\gamma} \max_{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}} \left(\left\vert \mathbf{z}_{\mathbf{sa}}^{\top} \mathbf{w}_r - \mathbb{E}_{r \mid \mathbf{s}, \mathbf{a}}[r ( \mathbf{s}, \mathbf{a}) ] \right\vert + \max_i \left\vert \mathbf{w}_i \right\vert \sum \left\vert \mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d -\mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime} \mid \mathbf{s}, \mathbf{a}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}\right] \right\vert \right) $$ where $\max_i \left\vert \mathbf{w}_i \right\vert$ is the maximum of the elements in the vector $\mathbf{w}$.

$\mathbf{Proof.}$

Let $\mathbf{w}$ be the solution described in the previous theorem:

\[\mathbf{w}^* = \left( \mathbf{Z}^\top \mathbf{Z} - \gamma \mathbf{Z}^\top \mathbf{Z}^\prime \right)^{-1} \mathbf{Z} \mathbf{r}\]

Let $p^\pi (\mathbf{s}, \mathbf{a})$ be the discounted state-action visitation distribution according to the policy $\pi$ starting from the state-action pair $(\mathbf{s}, \mathbf{a})$. Firstly, we have:

\[\begin{aligned} & \; \mathbf{w} = \left( \mathbf{I} - \gamma \mathbf{W}_d \right)^{-1} \mathbf{w}_r \\ \implies & \; \mathbf{w} - \gamma \mathbf{W}_d \mathbf{w} = \mathbf{w}_r \end{aligned}\]

Simplifying $\texttt{VE} (\mathbf{s}, \mathbf{a})$:

\[\begin{aligned} \texttt{VE}(\mathbf{s}, \mathbf{a}) := \; Q(\mathbf{s}, \mathbf{a}) - Q^\pi(\mathbf{s}, \mathbf{a}) \\ = & \; Q(\mathbf{s}, \mathbf{a}) - Q^\pi(\mathbf{s}, \mathbf{a}) \\ = & \; Q(\mathbf{s}, \mathbf{a}) - \mathbb{E}_{r, \mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[r+\gamma Q^\pi\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; Q(\mathbf{s}, \mathbf{a})-\mathbb{E}_{r, \mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[r+\gamma\left(Q\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)-\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right)\right] \\ = & \; Q(\mathbf{s}, \mathbf{a})-\mathbb{E}_{r, \mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[r+\gamma Q\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right]+\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; Q(\mathbf{s}, \mathbf{a})-\mathbb{E}_{r, \mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[r-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r+\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r+\gamma Q\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right]+\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; Q(\mathbf{s}, \mathbf{a})-\mathbb{E}_{r, \mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[r-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r+\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r+\gamma\left(\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top} \mathbf{w}-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}+\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}\right)\right] \\ & +\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; \mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}-\mathbb{E}_{r, \mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[r-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r+\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r+\gamma\left(\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top} \mathbf{w}-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}+\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}\right)\right] \\ & +\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; \mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}-\mathbb{E}_r\left[r-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r+\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r\right]-\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top} \mathbf{w}-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}+\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}\right] \\ & +\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; \mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r-\gamma \mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}-\mathbb{E}_r\left[r-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r\right]-\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top} \mathbf{w}-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}\right] \\ & + \gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; \mathbf{z}_\mathbf{sa}^{\top}\left(\mathbf{w}-\gamma \mathbf{W}_d \mathbf{w}-\mathbf{w}_r\right)-\mathbb{E}_r\left[r-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r\right]-\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top} \mathbf{w}-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}\right] \\ & +\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; -\mathbb{E}_r\left[r-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r\right]-\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top} \mathbf{w}-\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d \mathbf{w}\right]+\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] \\ = & \; \left(\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r-\mathbb{E}_r[r]\right)+\gamma\left(\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d-\mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top}\right]\right) \mathbf{w}+\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}}\left[\texttt{VE}\left(\mathbf{s}^{\prime}, \mathbf{a}^{\prime}\right)\right] . \end{aligned}\]

With the recursive relationship, the value error $\texttt{VE}$ recursively expands to the discounted state-action visitation distribution $p^\pi$. For $(\hat{\mathbf{s}}, \hat{\mathbf{a}}) \in \mathcal{S} \times \mathcal{A}$:

\[\texttt{VE} (\hat{\mathbf{s}}, \hat{\mathbf{a}}) = \frac{1}{1 - \gamma} \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim p^\pi (\hat{\mathbf{s}}, \hat{\mathbf{a}})} \left[ \left( \mathbf{z}_\mathbf{sa}^\top \mathbf{w}_r - \mathbb{E} [ r(\mathbf{s}, \mathbf{a}) ] \right) + \gamma \left( \mathbf{z}_\mathbf{sa}^\top \mathbf{W}_d - \mathbb{E}_{(\mathbf{s}^\prime, \mathbf{a}^\prime) \vert (\mathbf{s}, \mathbf{a})} \left[ \mathbf{z}_{\mathbf{s}^\prime \mathbf{a}^\prime}^\top \right] \right) \mathbf{w}\right]\]

Taking the absolute value, we finally obtain the theorem:

\[\begin{aligned} \vert\texttt{VE}(\hat{\mathbf{s}}, \hat{\mathbf{a}})\vert & =\left \vert \frac{1}{1-\gamma} \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim p^\pi(\hat{\mathbf{s}}, \hat{\mathbf{a}})}\left[\left(\mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r-\mathbb{E}_{r \mid \mathbf{s}, \mathbf{a}}[r]\right)+\gamma\left(\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d-\mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime} \mid \mathbf{s}, \mathbf{a}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top}\right]\right) \mathbf{w}\right]\right\vert \\ \vert\texttt{VE}(\hat{\mathbf{s}}, \hat{\mathbf{a}})\vert & \leq \frac{1}{1-\gamma} \mathbb{E}_{(\mathbf{s}, \mathbf{a}) \sim p^\pi(\hat{\mathbf{s}}, \hat{\mathbf{a}})}\left[\left \vert \mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r-\mathbb{E}_{r \mid \mathbf{s}, \mathbf{a}}[r]\right\vert+\gamma\left \vert \left(\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d-\mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime} \mid \mathbf{s}, \mathbf{a}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top}\right]\right) \mathbf{w}\right\vert\right] \\ & =\frac{1}{1-\gamma} \max _{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}}\left(\left \vert \mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r-\mathbb{E}_{r \mid \mathbf{s}, \mathbf{a}}[r]\right\vert+\gamma\left \vert \left(\mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d-\mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime} \mid \mathbf{s}, \mathbf{a}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}^{\top}\right]\right) \mathbf{w}\right\vert\right) \\ & \leq \frac{1}{1-\gamma} \max _{(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}}\left(\left \vert \mathbf{z}_\mathbf{sa}^{\top} \mathbf{w}_r-\mathbb{E}_{r \mid \mathbf{s}, \mathbf{a}}[r]\right\vert+\max _i\left \vert \mathbf{w}_i\right\vert \sum\left \vert \mathbf{z}_\mathbf{sa}^{\top} \mathbf{W}_d-\mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime} \mid \mathbf{s}, \mathbf{a}}\left[\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}\right]\right\vert\right) \end{aligned}\] \[\tag*{$\blacksquare$}\]

Building upon this theorem, we can directly learn the features $\mathbf{z}_\mathbf{sa}$ by jointly optimizing them together with the linear weights $\mathbf{w}_r$ and $\mathbf{W}_d$. This is achieved by treating the features and linear weights as a unified end-to-end model, and balancing the following losses with a hyperparameter $\lambda$:

\[\mathcal{L}(\mathbf{z}_{\mathbf{sa}}, \mathbf{w}_r, \mathbf{W}_d) = \underbrace{\mathbb{E}_\mathcal{D} \left[ \left( \mathbf{z}_\mathbf{sa}^\top \mathbf{w}_r - r (\mathbf{s}, \mathbf{a}) \right)^2 \right]}_{\text{reward learning}} + \lambda \underbrace{\mathbb{E}_\mathcal{D} \left[ \left( \mathbf{z}_\mathbf{sa}^\top \mathbf{W}_d - \mathbf{z}_{\mathbf{s}^\prime \mathbf{a}^\prime} \right)^2 \right]}_\text{dynamics learning}\]

However, the resulting loss has some notable drawbacks:

1. Dependency on $\pi$
   The dynamics target $\mathbf{z}_{\mathbf{s}^\prime \mathbf{a}^\prime}$ is non-stationary since it depends on an action $\mathbf{a}^\prime$ determined by the actor $\pi$, creating an undesirable interdependence between the policy and encoder.
2. Undesirable local minima
   Jointly optimizing both the features $\mathbf{z}_\mathbf{sa}$ and the dynamics target can lead to undesirable local minima, result in collapsed or trivial solutions when the dataset does not fully cover the state and action space or when the reward is sparse. (Bellman equation is meant to consider the entire MDP and all state-action pairs, and it can be satisfied exactly by infinitely many suboptimal solutions over an incomplete dataset.)

To address this issue, the theoretically grounded approach is further relaxed by (1) targeting state-dependent embedding \(\mathbf{z}_{\mathbf{s}^\prime}\) instead of \(\mathbf{z}_{\mathbf{s}^\prime \mathbf{a}^\prime}\) and (2) an introduction of a target network \(f_{\theta_\texttt{targ}} (\mathbf{s}^\prime)\) to generate the dynamics target $\bar{\mathbf{z}}_{\mathbf{s}^\prime}$:

\[\mathcal{L}(\mathbf{z}_{\mathbf{sa}}, \mathbf{w}_r, \mathbf{W}_d) = \mathbb{E}_\mathcal{D} \left[ \left( \mathbf{z}_\mathbf{sa}^\top \mathbf{w}_r - r (\mathbf{s}, \mathbf{a}) \right)^2 \right] + \lambda \mathbb{E}_\mathcal{D} [ ( \mathbf{z}_\mathbf{sa}^\top \mathbf{W}_d - \underbrace{\bar{\mathbf{z}}_{\mathbf{s}^\prime}}_{\text{adjustment}})^2]\]

However, in practice, we cannot assume there is a linear relationship between the embedding \(\mathbf{z}_{\mathbf{sa}}\) and the value function. The following theorem shows that the non-linear Q-function \(\hat{Q}(\mathbf{z}_{\mathbf{sa}})\) can still estimate the true Q-value $Q^\pi (\mathbf{s}, \mathbf{a})$ as long as the features \(\mathbf{z}_{\mathbf{sa}}\) are sufficiently rich:

$\color{red}{\mathbf{Theorem.}}$ Non-linear approximation of Q-value with MR.Q
Given functions $f_\theta (\mathbf{s}) = \mathbf{z}_\mathbf{s}$ and $g_\theta (\mathbf{z}_\mathbf{s}, \mathbf{a}) = \mathbf{z}_{\mathbf{sa}}$, suppose there exists functions $\hat{p}$ and $\hat{r}$ such that for all $(\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}$: $$ \mathbb{E} \left[\hat{r} (\mathbf{z}_{\mathbf{sa}}) \right] = \mathbb{E} \left[ r(\mathbf{s}, \mathbf{a}) \right] \quad \hat{p} (\mathbf{z}_{\mathbf{s}^\prime} \vert \mathbf{z}_\mathbf{sa}) = \sum_{\hat{\mathbf{s}}: \mathbf{z}_{\hat{\mathbf{s}}} = \mathbf{z}_{\mathbf{s}^\prime}} p (\hat{\mathbf{s}} \vert \mathbf{s}, \mathbf{a}) $$ Then, there exists a function $\hat{Q}$ (which does not necessarily have to be linear) that is exactly equal to the true Q-value function $Q^\pi$ over all possible state-action pairs: $$ \forall (\mathbf{s}, \mathbf{a}) \in \mathcal{S} \times \mathcal{A}: \quad \hat{Q} (\mathbf{z}_\mathbf{sa}) = Q^\pi (\mathbf{s}, \mathbf{a}) $$ for any policy $\pi$ where there exists a corresponding policy $\hat{\pi}(\mathbf{a} \vert \mathbf{z}_\mathbf{s}) = \pi(\mathbf{a} \vert \mathbf{s})$. Furthermore, the above condition also guarantees that the optimal policy $\pi^* (\mathbf{a} \vert \mathbf{s})$ is equals to an optimal policy network $\hat{\pi}^* (\mathbf{a} \vert \mathbf{z}_\mathbf{s})$: $$ \hat{\pi}^* (\mathbf{a} \vert \mathbf{z}_\mathbf{s}) = \pi^* (\mathbf{a} \vert \mathbf{s}) $$

$\mathbf{Proof.}$

We prove the theorem by induction on $n$-step dynamics. Let

\[\begin{aligned} Q_n^\pi (\mathbf{s}, \mathbf{a}) & = \sum_{t=0}^n \gamma^t \mathbb{E}_\pi \left[ r(\mathbf{s}_t, \mathbf{a}_t) \vert \mathbf{s}_0 = \mathbf{s}, \mathbf{a}_0 = \mathbf{a} \right] \\ \hat{Q}_n (\mathbf{z}_{\mathbf{sa}}) & = \sum_{t=0}^n \gamma^t \mathbb{E}_\pi \left[ \hat{r}(\mathbf{z}_{\mathbf{s}_t \mathbf{a}_t}) \vert \mathbf{s}_0 = \mathbf{s}, \mathbf{a}_0 = \mathbf{a} \right] \end{aligned}\]

First, by the assumption, we have:

\[Q_0^\pi (\mathbf{s}, \mathbf{a}) = \mathbb{E} \left[ r (\mathbf{s}, \mathbf{a}) \right] = \mathbb{E} \left[ \hat{r} (\mathbf{z}_{\mathbf{sa}}) \right]\]

Assuming \(Q_{n-1}^\pi (\mathbf{s}, \mathbf{a}) = \hat{Q}_{n-1} (\mathbf{z}_\mathbf{sa})\), by noting that \(\hat{p} (\mathbf{z} \vert \mathbf{z}_\mathbf{sa}) = 0$ if $\mathbf{z}\) is not in the range of \(\mathbf{z}_\mathbf{s} = f_\theta (\mathbf{s})\):

\[\begin{aligned} Q_n^\pi (\mathbf{s}, \mathbf{a}) & =\mathbb{E} [r(\mathbf{s}, \mathbf{a})] + \gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}} \left[ Q_{n-1}^\pi (\mathbf{s}^{\prime}, \mathbf{a}^{\prime}) \right] \\ & = \mathbb{E} [\hat{r}(\mathbf{s}, \mathbf{a})] + \gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}} \left[\hat{Q}_{n-1} (\mathbf{z}_{s^{\prime} a^{\prime}}) \right] \\ & = \mathbb{E} [\hat{r}(\mathbf{s}, \mathbf{a})] + \gamma \sum_{\mathbf{s}^{\prime} \in \mathcal{S}} \sum_{\mathbf{a}^{\prime} \in \mathcal{A}} p (\mathbf{s}^{\prime} \mid \mathbf{s}, \mathbf{a}) \pi (\mathbf{a}^{\prime} \mid \mathbf{s}^{\prime}) \hat{Q}_{n-1} (\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}) \\ & = \mathbb{E} [\hat{r}(\mathbf{s}, \mathbf{a})] + \gamma \sum_{\mathbf{z}_{\mathbf{s}^{\prime}}} \sum_{\mathbf{a}^{\prime} \in \mathcal{A}} \hat{p} (\mathbf{z}_{\mathbf{s}^{\prime}} \mid \mathbf{z}_\mathbf{sa}) \hat{\pi} (\mathbf{a}^{\prime} \mid \mathbf{z}_{\mathbf{s}^{\prime}}) \hat{Q}_{n-1} (\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}) \\ & =\hat{Q}_n (\mathbf{z}_{\mathbf{s a}}). \end{aligned}\]

Therefore, \(\hat{Q} (\mathbf{z}_\mathbf{sa}) = \lim_{n \to \infty} \hat{Q}_n (\mathbf{z}_\mathbf{sa}) = Q^\pi (\mathbf{s}, \mathbf{a})\) exists as \(\hat{Q}_n\) can be defined as a function of $\hat{p}$, $\hat{r}$, and $\hat{\pi}$ for all $n \in \mathbb{N}$.

Similarly, let $\pi$ be an optimal policy. Repeating the same arguments we see that:

\[\begin{aligned} Q_n^\pi (\mathbf{s}, \mathbf{a}) & = \mathbb{E} [r(\mathbf{s}, \mathbf{a})]+\gamma \mathbb{E}_{\mathbf{s}^{\prime}, \mathbf{a}^{\prime}} \left[ Q_{n-1}^\pi (\mathbf{s}^{\prime}, \mathbf{a}^{\prime}) \right] \\ & = \mathbb{E} [r(\mathbf{s}, \mathbf{a})] + \gamma \sum_{\mathbf{s}^{\prime} \in \mathcal{S}} p (\mathbf{s}^{\prime} \mid \mathbf{s}, \mathbf{a}) \max_{\mathbf{a}^{\prime} \in \mathcal{A}} Q_{n-1}^\pi (\mathbf{s}^{\prime}, \mathbf{a}^{\prime}) \\ & = \mathbb{E} [\hat{r}(\mathbf{s}, \mathbf{a})] + \gamma \sum_{\mathbf{z}_{\mathbf{s}^{\prime}}} \hat{p} (\mathbf{z}_{\mathbf{s}^{\prime}} \mid \mathbf{z}_{\mathbf{sa}}) \max_{\mathbf{a}^{\prime} \in \mathcal{A}} \hat{Q}_{n-1} (\mathbf{z}_{\mathbf{s}^{\prime} \mathbf{a}^{\prime}}) \\ & = \hat{Q}_n (\mathbf{z}_\mathbf{sa}) \end{aligned}\]

Therefore, there exists a function \(\hat{Q} (g_\theta (\mathbf{z}_\mathbf{s}, \mathbf{a})) = Q^* (\mathbf{s}, \mathbf{a})\), consequently, there exists an optimal policy:

\[\hat{\pi}^* (\mathbf{a} \vert \mathbf{z}_\mathbf{s}) = \underset{\mathbf{a} \in \mathcal{A}}{\arg \max} \; \hat{Q} (\mathbf{z}_\mathbf{sa})\] \[\tag*{$\blacksquare$}\]

References

[1] Fujimoto et al. “Towards General-Purpose Model-Free Reinforcement Learning”, ICLR 2025
[2] Hansen et al. “TD-MPC2: Scalable, Robust World Models for Continuous Control”, ICLR 2024
[3] Hafner et al. “Mastering Diverse Domains through World Models”, arXiv 2023
[4] Wang et al. “EfficientZero V2: Mastering Discrete and Continuous Control with Limited Data”, arXiv:2403.00564
[5] Fujimoto et al., “For SALE: State-Action Representation Learning for Deep Reinforcement Learning (TD7)”, NeurIPS 2023