[Representation Learning] The MoCo Family
Introduction
Due to the summation over negative examples in the denominator of the InfoNCE loss, it frequently exhibits sensitivity to the batch size employed during training. In practical scenarios, large batch sizes are needed to attain good representation with this loss, which may impose significant computational overhead. MoCo (Momentum Contrast) circumvents this limitation by decoupling the mini-batch size from the number of negatives via the introduction of dynamic queue-based dictionary. And the encoder of representations in dictionary is updated by momentum update (specifically, Exponential Moving Average, EMA) to maintain the consistent dictionary, so-called momentum encoder.
MoCo v1
Framework
Momentum Contrast (MoCo, He et al. 2019) formulates the contrastive learning as building dynamic dictionaries. The “keys” in the dictionary are sampled from data, and are represented by an encoder network. Then it trains encoders to perform dictionary look-up: an encoded “query” should be similar to its matching key and dissimilar to others, by minimizing the contrastive learning.
Given a query sample \(\mathbf{x}_q\), consider the query representation \(\mathbf{q} = f_q (\mathbf{x}_q)\) where $f_q$ is the encoder network. And consider a set of encoded samples \(\{\mathbf{k}_0, \mathbf{k}_1, \mathbf{k}_2, ...\}\) that are the key representations of a dictionary and encoded by momentum encoder $f_k$, i.e. \(\mathbf{k}_j = f_k (\mathbf{x}_j^{\mathbf{k}})\). Assume that there is a single key \(\mathbf{k}^+\) in the dictionary that $\mathbf{q}$ matches. Then, we define the InfoNCE contrastive loss with temperature $\tau$ over one positive and $N - 1$ negative samples:
\[\mathcal{L}_{\text{MoCo}, \mathbf{x}_q} = - \log \frac{\exp(\mathbf{q} \cdot \mathbf{k}^+ / \tau)}{\sum_{j=1}^N \exp(\mathbf{q} \cdot \mathbf{k}_j / \tau)}\]Note that the dictionary is dynamic in the sense that the keys are randomly sampled, and that the key encoder evolves during training. And the key of MoCo dictionary is to be maintained as a FIFO queue in which samples are progressively replaced. The current mini-batch is enqueued to the dictionary, and the oldest mini-batch in the queue is removed. It enables us to reuse representations of immediate preceding mini-batches of data and it is beneficial to the consistency, because the oldest keys are the most outdated and thus the least consistent with the newest ones.
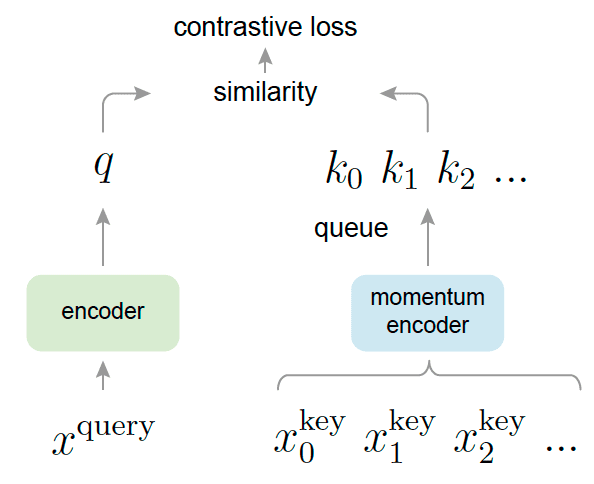
However, the queue-based dictionary is also intractable to update the key encoder by backpropagation, since the gradient should propagate to all samples in the large queue. From the result of ablation study ($\mathbf{Fig\ 5.}$), the paper hypothesize that good features can be learned by a large dictionary that covers a rich set of negative samples and the consistent key representation encoder. Consequently, MoCo leverages a momentum update with a momentum coefficient $m \in [0, 1)$ to train the momentum encoder:
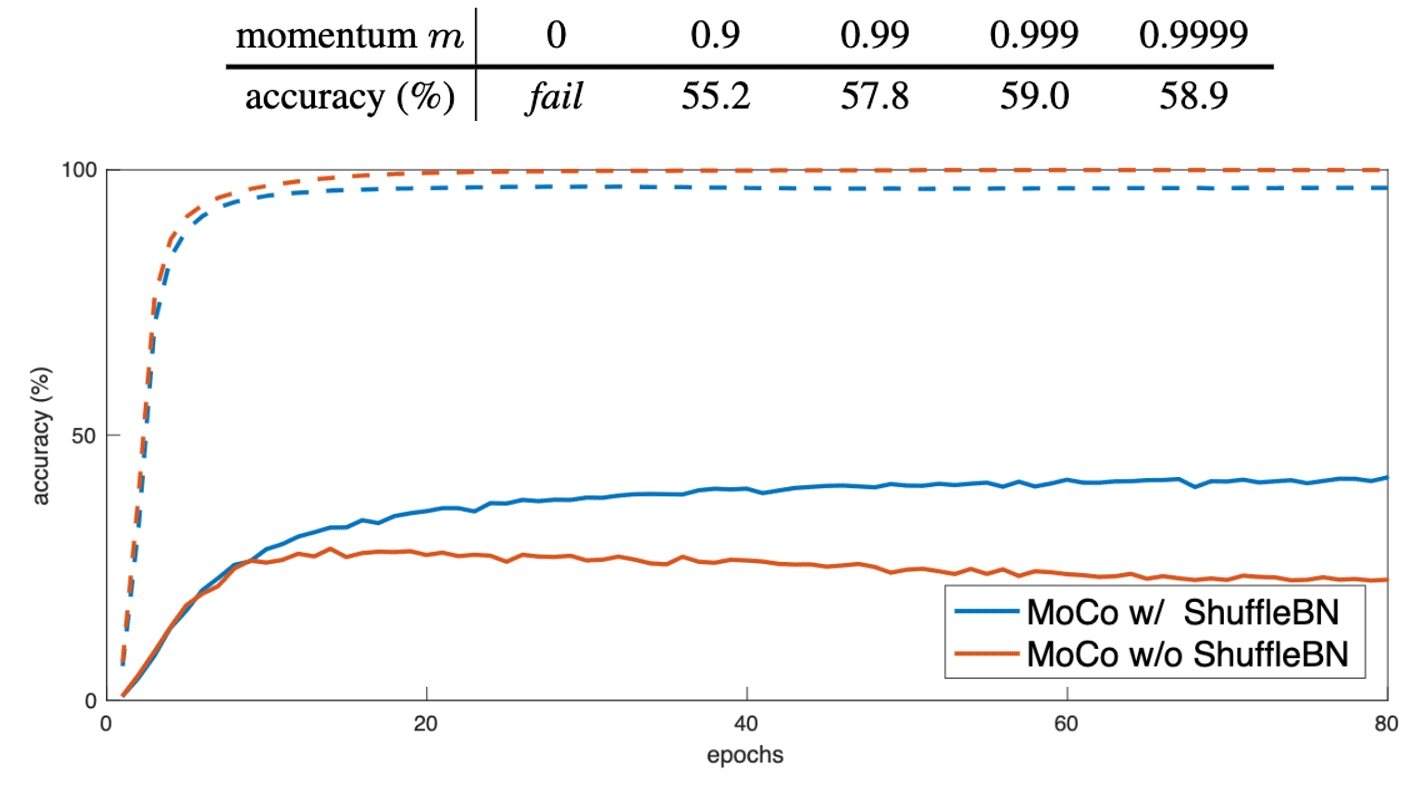
\[\theta_k \leftarrow m \theta_k + (1-m) \theta_q\]where $\theta_k$ are the parameters of $f_k$ and $\theta_q$ are those of $f_q$, updated by back-propagation. (In ablation, a relatively large momentum such as $m = 0.999$, works much better than a smaller value such as $m = 0.9$.)

Shuffling BN
In the paper, the encoders $f_q$ and $f_k$ both are ResNet, which have Batch Normalization (BN). The paper reports that BN leads to the information leak between samples in the same batch and hampers the learning of good representations. (See $\mathbf{Fig\ 5.}$) Ideally, during the feature learning process, the model should not perceive other samples within the same batch, ensuring that sample features are extracted independently. Otherwise the model can adopt some shortcuts to fulfill the contrastive task.
To interrupt the intra-batch communication among samples, MoCo employs shuffling BN. It is trained with multiple GPUs and perform BN on the samples independently for each GPU. Furthermore, it shuffles the sample order in the current mini-batch for the key encoder $f_k$ (and shuffle back after encoding), while the sample order for the query encoder $f_q$ is not altered.
Results
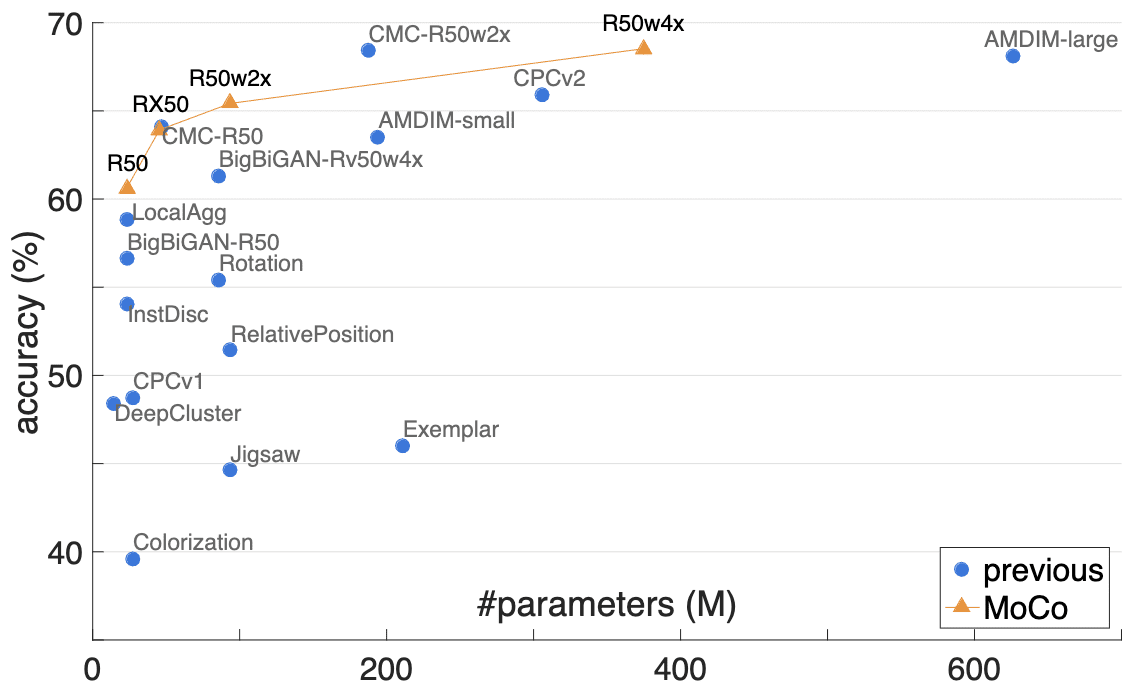
As a result, MoCo with ResNet50 performs competitively and achieves 60.6% accuracy, better than all competitors of similar model size. Also, MoCo benefits from larger models and achieves 68.6% accuracy with ResNet50 with widening factors $16\times$ (R50w$4\times$).
More importantly, the representations learned by MoCo transfer well to downstream tasks. MoCo can outperform its supervised pre-training counterpart in 7 detection/segmentation tasks on PASCAL VOC, COCO, and other datasets, sometimes surpassing it by large margins. For more detail, please refer to the original paper [1].
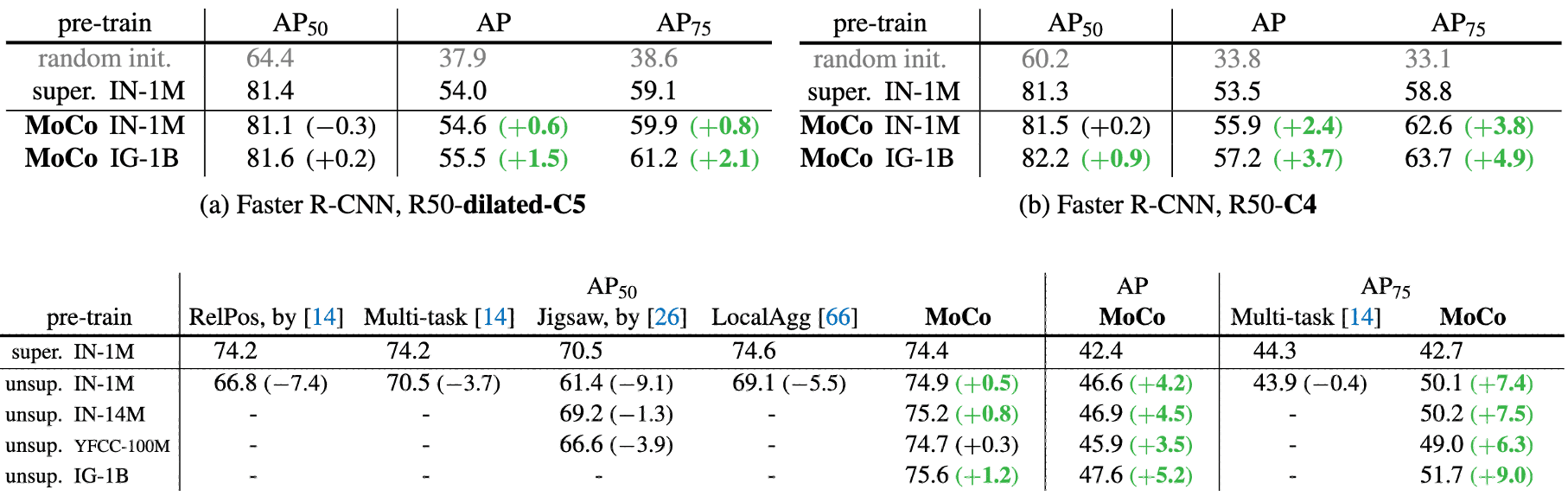
In the brackets are the gaps to the ImageNet supervised pre-training counterpart. (He et al. 2020)
Finally, here are ablations on momentum coefficient $m$ (Top) and shuffling BN (Bottom).
MoCo v2
Framework
MoCo v2 (Chen et al. 2020) is the improved version of MoCo with simple modifications based on SimCLR, namely, using an MLP projection head and stronger data augmentation.
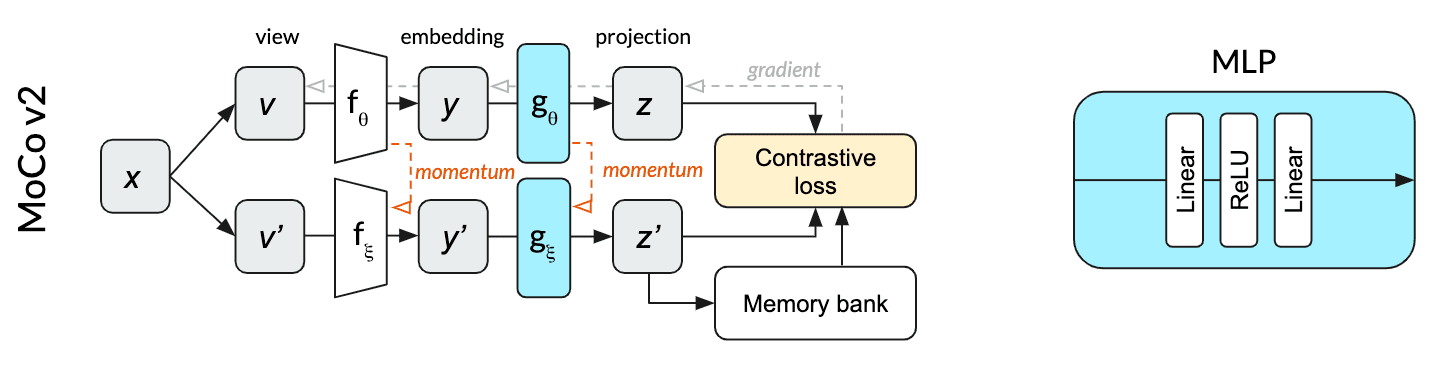
The contrastive learning can be achieved by various mechanisms that differ in how the keys are maintained. In an end-to-end mechanism such as SimCLR, the negative keys are from the same batch and updated end-to-end by back-propagation, leading to the need for large batch size to provide a large set of negatives. But note that owing to the memory queue, MoCo decouples the batch size from the number of negatives and hence a large number of negative samples are readily available.
Result
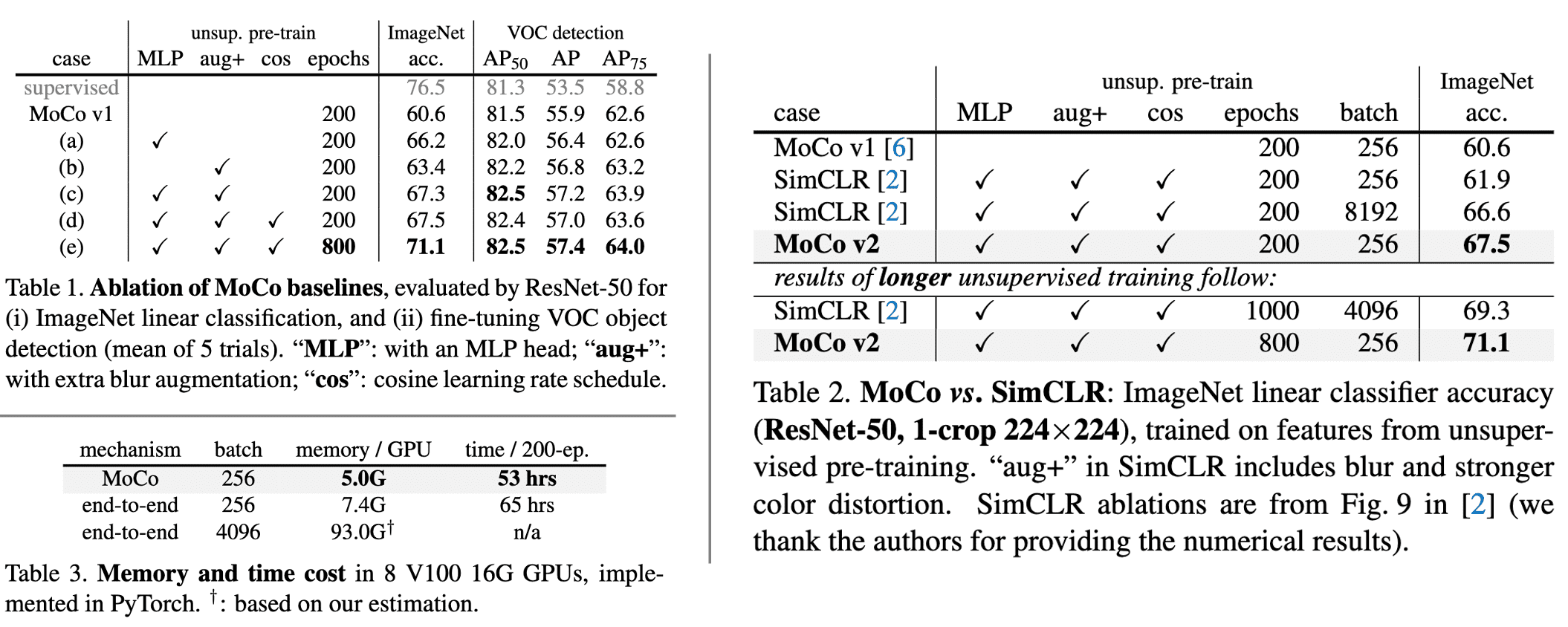
$\mathbf{Table\ 1}$ in $\mathbf{Fig\ 7}$ shows the ablation study of MoCo v2. The original augmentation in Moco v1 is extended by including the blur augmentation in SimCLR. (Stronger color distortion in SimCLR has been removed as it degrades the performance of MoCo v2.) With the MLP projection head, the extra augmentation boosts ImageNet accuracy to 67.3%. Furthermore, the table implies that linear classification accuracy is not monotonically related to transfer performance in detection.
$\mathbf{Table\ 2}$ compares SimCLR with MoCo v2 and MoCo v2 achieves 71.1%, outperforming SimCLR’s 69.3% with 1000 epochs. Also, $\mathbf{Table\ 3}$ shows the memory and time cost of MoCo v2. Note that the end-to-end case reflects the SimCLR cost in GPUs. The end-to-end variant is more costly in both aspects, since it back-propagates to both $\mathbf{q}$ and $\mathbf{k}$ encoders, while MoCo framework back-propagates to the $\mathbf{q}$ encoder only.
References
[1] He et al. “Momentum Contrast for Unsupervised Visual Representation Learning”, CVPR 2020
[2] Different understanding of Shuffling BN, GitHub Issues
[3] Chen et al. “Improved Baselines with Momentum Contrastive Learning”, arXiv preprint arXiv:2003.04297, 2020.

Leave a comment